2019.10.22 csp-s模拟测试82 反思总结

重来重来，刚刚就当什么都没发生

今天的题属实有些迷惑，各种意义上…总之都很有难度吧。不满归不满，这套题的确不是什么没有意义的题目。

为了考验自己的学习能力记忆力，决定不写题解，扔个代码完事了

其实是懒得写一大堆式子的推理以及想表示一下对出题人的敬意

你就不怕你到时候回来看一脸懵逼吗

T1：

#include<iostream>
#include<cstdio>
using namespace std;
int t,mod=,mod1=;
long long n;
int main()
{
    scanf("%d",&t);
    long long num=,x=;
    while(mod1){
        if(mod1&)num=num*x%mod;
        x=x*x%mod;
        mod1>>=;
    }
    while(t--){
        scanf("%lld",&n);
        n%=mod;
        printf("%lld\n",(n*n%mod-)*num%mod);
    }
    return ;
}

T2：

这题考场上出70分思路挺快的，大概20min或者更少，连带读完三道题的时间…这个思路本质上也是推导正解的中间过程

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+;
int n,len,nxt[*N],lons;
long long ans,num1[*N],num2[*N];
char s[*N],c[*N],a[*N],ss[*N];
void kmp1(int lon){
    strcpy(a+lon+,s+);
    a[lon+]='.';
    int lens=strlen(a+);
    for(int i=;i<=lens;i++)nxt[i]=;
    for(int i=;i<=lens;i++){
        int j=nxt[i-];
        while(j&&a[j+]!=a[i])j=nxt[j];
        if(a[j+]==a[i])nxt[i]=j+;
        if(nxt[i]==lon)num1[i-*lon]++;
    }
}
void kmp2(int lon){
    strcpy(a+lon+,s+);
    a[lon+]='.';
    int lens=strlen(a+);
    for(int i=;i<=lens;i++)nxt[i]=;
    for(int i=;i<=lens;i++){
        int j=nxt[i-];
        while(j&&a[j+]!=a[i])j=nxt[j];
        if(a[j+]==a[i])nxt[i]=j+;
        if(nxt[i]==lon)num2[i-lon-]++;
    }
}
int main()
{
    scanf("%s",s+);
    lons=strlen(s+);
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%s",c+);
        len=strlen(c+);
        for(int j=;j<=len;j++){
            strcpy(a+,c+);
            strcpy(a+j+,ss+);
            kmp1(j);
            strcpy(a+,c+j);
            strcpy(a+len-j+,ss+);
            kmp2(len-j+);
        }
    }
    for(int i=;i<=lons;i++){
        ans+=num1[i]*num2[i-];
    }
    printf("%lld\n",ans);
    return ;
 } 

考场70pts

这个70分的做法是，读入一个字符串以后，暴力地扫出它的所有前后缀，对每一个前后缀在s串上跑一下kmp。如果是后缀，就在s串匹配成功的位置让计数器cnt2++。如果是前缀，就在s串匹配成功的子串的开始位置让计数器cnt1++。

最后扫一遍计数器数组（到s串的长度），ans+=cnt2_i*cnt1_i+1。

应该是正解里最基础的那部分吧。

能想到正解的一部分对于一个菜鸡来说太不容易了赶紧详细写一下【？】

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+,p=,mod=;
int n,len,cnt1=,cnt2=,lens;
char s[*N],c[*N];
int tree1[*N][],tree2[*N][];
unsigned long long hash1[*N],hash2[*N],ks[*N];
long long ans;
struct node{
    int m;
    #define m 1500007
    int head[][m+],Next[][*N],tot[];
    long long siz[][*N];
    unsigned long long ver[][*N];
    void ins(unsigned long long has,int opt,long long sum){
        unsigned long long x=has%m;
        for(int i=head[opt][x];i;i=Next[opt][i]){
            if(has==ver[opt][i]){
                siz[opt][i]+=sum;
                return;
            }
        }
        ver[opt][++tot[opt]]=has,siz[opt][tot[opt]]=sum,Next[opt][tot[opt]]=head[opt][x],head[opt][x]=tot[opt];
        return;
    }
    long long get(unsigned long long has,int opt){
        unsigned long long x=has%m;
        for(int i=head[opt][x];i;i=Next[opt][i]){
            if(has==ver[opt][i]){
                return siz[opt][i];
            }
        }
        return ;
    }
}h;
void insert(){
    int now=;
    unsigned long long has=;
    for(int i=;i<=len;i++){//前缀
        has=has*p+c[i];
        if(!tree1[now][c[i]-'a'])tree1[now][c[i]-'a']=++cnt1;
        h.ins(has,,);
        now=tree1[now][c[i]-'a'];
    }
    now=,has=;
    for(int i=len;i>=;i--){//后缀
        has=has*p+c[i];
        if(!tree2[now][c[i]-'a'])tree2[now][c[i]-'a']=++cnt2;
        h.ins(has,,);
        now=tree2[now][c[i]-'a'];
    }
}
void dfs1(int now,unsigned long long has){
    for(int i=;i<;i++){
        if(tree1[now][i]){
            long long val=has*p+i+'a';
            long long sum=h.get(has,);
            h.ins(val,,sum);
            dfs1(tree1[now][i],val);
        }
    }
}
void dfs2(int now,unsigned long long has){
    for(int i=;i<;i++){
        if(tree2[now][i]){
            long long val=has*p+i+'a';
            long long sum=h.get(has,);
            h.ins(val,,sum);
            dfs2(tree2[now][i],val);
        }
    }
}
long long work(int x){
    int l=,r=x,ans1=,ans2=;
    while(l<=r){//后缀
        int mid=(l+r)/;
        unsigned long long val=hash2[mid]-hash2[x+]*ks[x-mid+];
        long long sum=h.get(val,);
        if(sum){
            ans2=sum;
            r=mid-;
        }
        else l=mid+;
    }
    l=x+,r=lens;
    while(l<=r){//后缀
        int mid=(l+r)/;
        unsigned long long val=hash1[mid]-hash1[x]*ks[mid-x];
        long long sum=h.get(val,);
        if(sum){
            ans1=sum;
            l=mid+;
        }
        else r=mid-;
    }
    return 1ll*ans1*ans2;
}
int main()
{
    scanf("%s",s+);
    lens=strlen(s+);
    ks[]=;
    for(int i=;i<=lens;i++){
        hash1[i]=hash1[i-]*p+s[i];
        ks[i]=ks[i-]*p;
    }
    for(int i=lens;i>=;i--){
        hash2[i]=hash2[i+]*p+s[i];
    }
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%s",c+);
        len=strlen(c+);
        insert();
    }
    dfs1(,);
    dfs2(,);
    for(int i=;i<lens;i++){
        ans+=work(i);
    }
    printf("%lld\n",ans);
    return ;
}

很神奇的思路转化：让一个中间点前面衔接的最长后缀代表所有更靠近中间点的后缀，记录一个前缀和。因为不用考虑每个前后缀具体的位置，只要存在包含它的更长前后缀就一定能同时对答案产生贡献，所以可以利用trie树来统计一下前缀和。就trie树的操作过程来说，的确非常适合统计数量的前缀和信息。用hash映射所有存在的前后缀，在每个中间点记录答案的时候二分这个最长前后缀。相当于用hash和trie树替代掉了原本一次次跑kmp匹配的过程，非常优秀。

关于我为什么这么生气的原因，这题在hash上搞幺蛾子？嗯？

大概率是我菜吧

记一下要点：巩固一下ull自然溢出，以及哈希表

哈希表本质是利用关键字的分类（散列函数映射）来加速查询

T3：

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int mod=3e5+;
int t;
ll n,m,k,ans,rec[mod+],inv[mod+],minn;
ll ksm(ll x,int k){
    ll num=;
    while(k){
        if(k&)num=num*x%mod;
        x=x*x%mod;
        k>>=;
    }
    return num;
}
void work(){
    inv[]=rec[]=rec[]=;
    for(int i=;i<=mod-;i++)rec[i]=rec[i-]*i%mod;
    inv[mod-]=ksm(rec[mod-],mod-);
    for(int i=mod-;i>=;i--)inv[i]=inv[i+]*(i+)%mod;
}
ll cal(ll x,ll y){
    if(x<y)return ;
    if(!y||!x)return ;
    return rec[x]*inv[y]%mod*inv[x-y]%mod;
}
ll C(ll x,ll y){
    if(x<y)return ;
    if(!y)return ;
    return C(x/mod,y/mod)*cal(x%mod,y%mod)%mod;
}
int main()
{
    scanf("%d",&t);
    work();
    while(t--){
        scanf("%lld%lld%lld",&n,&m,&k);
        if(k==){
            n%=mod,m%=mod;
            printf("%lld\n",n*m%mod);
            continue;
        }
        minn=min(n,m);
        ans=;
        if(n>m)swap(n,m);
        ans=(ans+n%mod*C(m,k)%mod+m%mod*C(n,k))%mod;
        ans=(ans+*(*C(n,k+)%mod+(m-n+)%mod*C(n,k))%mod)%mod;
        if(k==){
            minn%=mod;
            long long n1=n,m1=m;
            n%=mod,m%=mod;
            minn=((min(n1,m1)-)/)%mod;
            ans=(ans+*(minn*n%mod*m%mod-*(+minn)%mod*minn%mod*inv[]%mod*(m+n)%mod+*minn%mod*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
        }
        else if(k==){
            minn%=mod;
            long long n1=n,m1=m;
            n%=mod,m%=mod;
            ans=(ans+(minn*n%mod*m%mod-(+minn)*minn%mod*inv[]%mod*(m+n)%mod+minn*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
            minn=min(m1/,n1)%mod;
            ans=(ans+*(minn*n%mod*m%mod-(+minn)*minn%mod*inv[]%mod*(m+*n)%mod+*minn%mod*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
            swap(n1,m1);
            swap(n,m);
            minn=min(m1/,n1)%mod;
            ans=(ans+*(minn*n%mod*m%mod-(+minn)*minn%mod*inv[]%mod*(m+*n)%mod+*minn%mod*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
            minn=((min(n1,m1)-)/)%mod;
            ans=(ans+*(minn*n%mod*m%mod-*(+minn)%mod*minn%mod*inv[]%mod*(m+n)%mod+*minn%mod*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
        }
        else if(k==){
            minn%=mod;
            long long n1=n,m1=m;
            n%=mod,m%=mod;
            ans=(ans+*(minn*n%mod*m%mod-(+minn)*minn%mod*inv[]%mod*(m+n)%mod+minn*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
            minn=min(m1/,n1)%mod;
            ans=(ans+*(minn*n%mod*m%mod-(+minn)*minn%mod*inv[]%mod*(m+*n)%mod+*minn%mod*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
            swap(n1,m1);
            swap(n,m);
            minn=min(m1/,n1)%mod;
            ans=(ans+*(minn*n%mod*m%mod-(+minn)*minn%mod*inv[]%mod*(m+*n)%mod+*minn%mod*(minn+)%mod*(*minn+)%mod*ksm(,mod-)%mod+mod)%mod)%mod;
        }
        printf("%lld\n",ans);
    }
    return ;
}
/*
3
7 7 3
7 6 3
8 9 3

1
5 5 1
*/

记一下平方和公式：

差点忘了这个：

朱世杰恒等式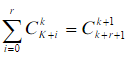

其实它和平方和公式也有点联系