深度优先搜索DFS---最优子序列求和问题（1）

题目：

　　给定N 个整数（可能有负数），从中选择 K个数，使得这 K个数之和恰好等于一个给定的整数 X；如果有多种方案，那么选择它们中元素平方和最大的一个。例如，从4个整数｛ 2， 3， 3 ，4｝中选择 2个数（集合中的每一个数只能被选一次），使它们的和为 6。显然有两种方案｛2，4｝和｛3， 3｝，其中平方和最大的方案为｛2， 4｝。数据保证存在且唯一。

输入格式：

第一行给出 一个正整数 N( 1<=N<=20)

第二行给出N个整数（可能有正有负，可能不按数的大小顺序给出），中间以空格隔开。

第三行给出选择元素 K个数 ，以及它们的和 X

输出格式：

按递增的方式输出序列。

输入样例：

4   //4个元素

2 3 3 4 //4个元素的值

2 6 //选择 2个元素，之和为 6

输出样例

2 4

直接给出代码。

自我规定：当有多个递归边界时，通常把”判断是否是答案“的条件作为递归边界一。

 #include<iostream>
 #include<vector>
 #include<algorithm>
 using namespace std;

 const int maxn = ;
 int A[maxn] = {};
 int n,k,x,maxSumSqu= -;
 vector<int> temp,ans;
 void DFS(int index, int nowK,int sum,int sumSqu) {
     if(nowK == k && sum == x) {//递归边界一
         if(maxSumSqu < sumSqu) {
             maxSumSqu = sumSqu;
             ans = temp; //vector之间等号赋值，仅限 Int
         }
         return ;
     }
     if(index == n || nowK > k || sum > x) return ;//递归边界二
     temp.push_back(A[index]);
     DFS(index+,nowK+1,sum+A[index],sumSqu+A[index]*A[index]);    //"选择"index号数
     temp.pop_back();
     DFS(index+,nowK,sum,sumSqu);//"不选择"index号数
 }

 int main() {
     cin>>n;
     for(int i = ; i < n; ++i)
         cin>>A[i];
     cin>>k>>x;
     DFS(,,,);//初始参数一般都为 0
     sort(ans.begin(),ans.end());
     for(int i = ; i < ans.size(); ++i) {
         if(i > ) printf(" ");
         printf("%d",ans[i]);
     }
     return ;
 }

运行结果：

题目修改：

假设 N个整数中的每一个都可以被选择多次，那么选择 K个数，使得 K个数之和恰好为X。

只需修改一处代码即可，那么可以持续选择index号数，直至不再选择index号数，再转入“不选index号数”的分支。

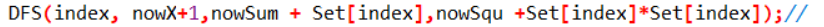
 #include<iostream>
 #include<vector>
 #include<algorithm>
 using namespace std;

 const int maxn = ;
 int Set[maxn] = {};
 int n,x,sum,MAXSqu= -;
 vector<int> temp,ans;
 void DFS(int index, int nowX,int nowSum,int nowSqu) {
     if(nowX == x && nowSum == sum) {//递归边界一
         if(MAXSqu < nowSqu) {
             MAXSqu = nowSqu;
             ans = temp; //vector之间等号赋值，仅限 Int
         }
         return ;
     }
     if(index == n || nowX > x || nowX > sum) return ;//递归边界二 

     temp.push_back(Set[index]);//保存当前元素
     DFS(index, nowX+,nowSum + Set[index],nowSqu +Set[index]*Set[index]);//“选择”当前 index号数
     temp.pop_back();
     DFS(index + ,nowX,nowSum,nowSqu); //“不选择”当前 index 号数
 }

 int main() {
     cin>>n;
     for(int i = ; i < n; ++i)
         cin>>Set[i];
     cin>>x>>sum;
     DFS(,,,);
     sort(ans.begin(),ans.end());
     for(int i = ; i < ans.size(); ++i) {
         if(i > ) printf(" ");
         printf("%d",ans[i]);
     }
     return ;
 }