动态连通性问题：union-find算法

写在前面的话：

一枚自学Java和算法的工科妹子。

• 算法学习书目：算法（第四版） Robert Sedgewick
• 算法视频教程：Coursera  Algorithms Part1&2

本文是根据《算法（第四版）》的个人总结，如有错误，请批评指正。

一、动态连通性问题介绍

1.基本概念：

• 问题的输入是一列整数对，每个整数都表示一个某种类型的对象，一对整数“p q”表示的含义是“p和q相连”。
• “相连”是一种等价关系：1）自反性（p与p相连接）；2）对称性（若p连接到q，那么q也连接到p）；3）传递性（若p连接到q，q连接到r，则p连接到r）。
• 等价关系将对象分成多个等价类，它们构成多个集合，称为“连通组件”（Connected Components）。

2.目标：设计一个程序，保存所有的整数对信息，并判断一对输入的对象是否相连。

3.应用：

• 计算机网络。若这些数字编号的对象是大型计算机网络中的各计算机设备，点对序列即表示了计算机之间的通信连接。因此我们的算法能够判断对于某两台计算机p和q，要使它们能够互相通信，是需要建立新的连接，还是可以利用已有的线路建立一个通信路径。
• 社交网络。数字编号的物体代表Facebook上的用户，而点对表示朋友关系，那么我们的算法就可以在两个用户之间建立朋友关系，或者查找他们俩有没有“可能认识的人”。
• 变量名的等价性。在某些编程语言中，可以用我们的算法来检测某两个变量是否是等价的（都指向同一对象）。
• 数学上的集合论。可以判断某两个整数是否属于同一集合。

 

二、动态连通性问题分析和建模

     动态连通性问题只要求判断给定的整数p和q是否连通，并不要求给出两者之间的所有连接。设计并查集算法的API封装以下操作：初始化，连接两个对象，查找某对象所在的集合的标识符，判断两对象是否相连，统计连通集合的数目。

图1 并查集算法的API设计

解决连通性问题就是实现并查集算法的API：

• 定义一种数据结构表示已知的连接；
• 基于此数据结构实现高效的union()，find()，connected()，count().

三、union-find算法的实现

下面讨论四种不同的实现，它们均以id[]数组来确定两个对象是否存在于相同的连通分量。

1.quick-find算法

• quick-find算法是保证当且仅当id[p]=id[q]时p和q是连通的，因此同一个连通集合的所有对象的id全部相同。
• find(p)：返回p的id，同一个连通集合的所有对象的id全部相同；
• connected(p,q)：判断id[p]==id[q]?
• union(p,q)：先用 connected(p,q)判断p和q是否相连，若不相连（p所在集合的id为一个值，q所在集合的id为另一个值），遍历数组所有元素，将p所在集合的对象的id全部改为id[q].

图2 quick-find算法:find(5,9)和union(5,9)

 public class QuickFindUF {
     private int[] id;    // 对象的id
     private int count;   // 连通集合数量
 
    // 初始化对象id数组
     public QuickFindUF(int n) {
         count = n;
         id = new int[n];
         for (int i = 0; i < n; i++)
             id[i] = i;
     }
 
    // 返回连通集合数量
     public int count() {
         return count;
     }
 
    // 返回对象p的id
     public int find(int p) {
         return id[p];
     }
 
    // 判断p和q是否相连
     public boolean connected(int p, int q) {
         validate(p);
         validate(q);
         return id[p] == id[q];
     }
 
    // 将p和q归并到同一个集合
     public void union(int p, int q) {
         validate(p);
         validate(q);
         int pID = id[p];   // needed for correctness
         int qID = id[q];   // to reduce the number of array accesses
 
         // p q已经在同一个集合则不需要采取任何行动
         if (pID == qID) return;
 
         // 将p所在的集合的所有对象重新赋值id为id[q]
         for (int i = 0; i < id.length; i++)
             if (id[i] == pID) id[i] = qID;
         count--;
     }
 
 }

quick-find算法分析（含有N个对象）：

• 每次find()调用只需访问数组一次；
• 每次归并两个集合的union()操作需要访问数组次数在（N+3）~（2N+1）之间。（最好的情况p所在集合只有p一个对象：2+N+1=N+3,最坏情况除了q以后所有对象都在p所在集合：2+N+N-1=2N+1）

因此使用quick-find算法解决动态连通性问题并且最后使所有对象都在一个连通集合，至少需要调用N-1次union()，即至少(N+3)(N-1)~N²次访问数组。

2.quick-union算法

• quick-find算法的union操作需要遍历整个数组才能完成，为提高union()方法的速度，提出quick-union算法。
• quick-union算法的策略：parent[p]为节点p的父节点，若id[p] == p，则称p为根节点（root），当且仅当两个节点的根节点相等时，两个节点处于同一连通集合中。那么初始状态下的N个节点就可以看成N棵只有一个节点的树构成的“森林”，而id数组则记录了每个节点的父节点，若两个节点的根节点相等，那么这两个节点就是相连接的。
• find(p)：沿着路径一直向上回溯，直到找到根节点parent[r] == r；
• union(p,q)：先找到节点p和q各自的根节点pRoot和qRoot，然后修改p的父节点parent[p]=qRoot。

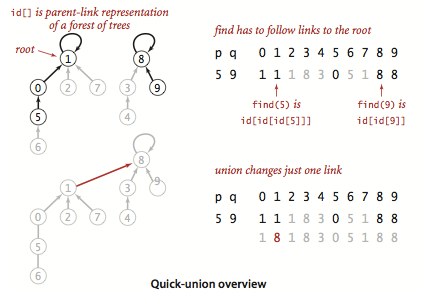
图3 quick-union算法:find(5,9)和union(5,9)

 public class QuickUnionUF {
     private int[] parent;  // 父节点
     private int count;     // 连通集合数目
 
     public QuickUnionUF(int n) {
         parent = new int[n];
         count = n;
         for (int i = 0; i < n; i++) {
             parent[i] = i;
         }
     }
 
     public int count() {
         return count;
     }
 
     public int find(int p) {
         while (p != parent[p])
             p = parent[p];
         return p;
     }
 
     public boolean connected(int p, int q) {
         return find(p) == find(q);
     }
 
     public void union(int p, int q) {
         int rootP = find(p);
         int rootQ = find(q);
         if (rootP == rootQ) return;
         // 将p所在的树连接到q的根节点rootQ上
         parent[rootP] = rootQ;
         count--;
     }
 
 }

quick-union算法分析（含有N个节点）：

• union()：所有节点全部归并到一个集合，最坏的情况就是0连接到1,1连接到2,2连接到3...如此循环，构造0-1-2-3-4……-N-1形式的一棵很“高”的树，根节点是N-1，总共访问数组的次数(N-1)+2[1+2+...+(N-1)]+(N-1)~N²
• 前面的(N-1)表示像树上每增加一个节点i(i=1,2,3,...,N-1)，find(i)访问数组的总次数；
• 中间的2[1+2+...+(N-1)]表示对树尾部的节点0，find(0)访问数组的总次数；
• 最后的(N-1)表示将节点0的根节点设为i(i=1,2,3,...,N-1)，访问数组的总次数.

3.加权quick-union算法

• 加权quick-find算法在quick-find算法修改程序，避免出现高度很高的树。一种加权策略就是记录每棵树的节点个数，并总是在执行union操作时用小树（节点较少）的根节点指向大树（节点较多）来保持平衡。
• 加权quick-find算法策略：增加一个数组sz[]来存储每棵树的节点个数，一开始将sz[]全部初始化为1，每次执行union操作时根据sz[]数组进行判断，将小树根节点指向大树的根节点，并更新大树对应的sz[]值。

图4 加权quick-find算法降低树高度

 public class WeightedQuickUnionUF {
     private int[] parent;   // parent[i] = parent of i
     private int[] size;     // size[i] = number of sites in subtree rooted at i
     private int count;      // number of components
 
     public WeightedQuickUnionUF(int n) {
         count = n;
         parent = new int[n];
         size = new int[n];
         for (int i = 0; i < n; i++) {
             parent[i] = i;
             size[i] = 1;
         }
     }
 
     public int count() {
         return count;
     }
 
     public int find(int p) {
         while (p != parent[p])
             p = parent[p];
         return p;
     }
 
     public boolean connected(int p, int q) {
         return find(p) == find(q);
     }
 
     public void union(int p, int q) {
         int rootP = find(p);
         int rootQ = find(q);
         if (rootP == rootQ) return;
 
         // make smaller root point to larger one
         if (size[rootP] < size[rootQ]) {
             parent[rootP] = rootQ;
             size[rootQ] += size[rootP];
         }
         else {
             parent[rootQ] = rootP;
             size[rootP] += size[rootQ];
         }
         count--;
     }
 }

加权quick-union算法分析（含有N个节点）：

• 对于N个节点，加权quick-union算法构造的森林中任意节点的深度最多为lgN（由归纳算法推到得，不明白的朋友可以留言或发邮件询问）
• 因此，在最坏的情况下，find()、connected()和union()的成本增长数量级为lgN。

4.路径压缩的加权quick-union算法

• 理想情况下，希望每个节点都直接连接在它的根节点上，但是又不像quick-find那样union方法要遍历所有节点。要实现路径压缩，只需要为find()添加一个循环，将在路径上遇到的所有点都直接连接到根节点。
• 路径压缩的加权quick-union算法已经是最优的算法了，但是并非所有的操作都能在常数时间内完成。

 public class PathCompressWQU {
     private int[] parent;   // parent[i] = parent of i
     private int[] size;     // size[i] = number of sites in subtree rooted at i
     private int count;      // number of components
 
     public PathCompressWQU(int n) {
         count = n;
         parent = new int[n];
         size = new int[n];
         for (int i = 0; i < n; i++) {
             parent[i] = i;
             size[i] = 1;
         }
     }
 
     public int count() {
         return count;
     }
 
     public int find(int p) {
         int temp=p;
         while (p != parent[p])
             p = parent[p];
 
         while(temp != parent[p]){
             int tempParent = parent[temp];
             parent[temp] = parent[p];
             temp = tempId;
           }
 
         return parent[p];
     }
 
     public boolean connected(int p, int q) {
         return find(p) == find(q);
     }
 
     public void union(int p, int q) {
         int rootP = find(p);
         int rootQ = find(q);
         if (rootP == rootQ) return;
 
         // make smaller root point to larger one
         if (size[rootP] < size[rootQ]) {
             parent[rootP] = rootQ;
             size[rootQ] += size[rootP];
         }
         else {
             parent[rootQ] = rootP;
             size[rootP] += size[rootQ];
         }
         count--;
     }
 }

四、四种union-find算法的性能对比

作者： 邹珍珍（Pearl_zhen）

出处： http://www.cnblogs.com/zouzz/

声明：本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出 原文链接 如有问题， 可邮件（zouzhenzhen@seu.edu.cn）咨询.