InnoDB存储引擎的B+树索引算法

关于B+树数据结构

①InnoDB存储引擎支持两种常见的索引。

一种是B+树，一种是哈希。

B+树中的B代表的意思不是二叉（binary），而是平衡（balance），因为B+树最早是从平衡二叉树演化来的，但是B+树又不是一个平衡二叉树。

同时，B+树索引并不能找到一个给定键值的具体行。B+树索引只能找到的是被查找数据行所在的页。然后数据库通过把页读入内存，再在内存中进行查找，最后得到查找的数据。

再说一下平衡二叉树：

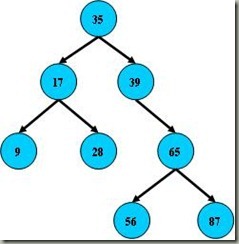
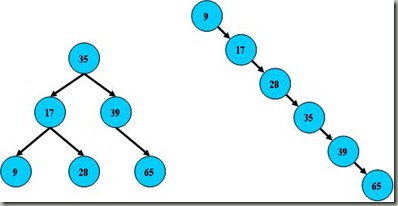
这是一幅平衡二叉树，左子树的值总是小于根的值，右子树的值总是大于根的键值，因此可以通过中序遍历（以递归的方式按照左中右的顺序来访问子树），因此遍历以后得到的输出是9、17、28、35、39、56、65、87。这样，如果要查找键值为28的记录，先找到根，然后发现根大于28，找左子树，发现左子树的根17小于28，再找下一层右子树，然后找到28。通过了3次查找找到了需要找的节点。但是如果二叉树节点分布非常不均匀，就像第二张图那样，那么如果要查找39这个节点的话，查找效率和顺序查找就差不多了，最差的结果就是查找65，那么二叉搜索树就会完全退化成线性表。因此如果想要最大性能地构造一个二叉查找树，需要这颗二叉查找树是平衡的，平衡二叉树对于查找的性能是比较高的，但是不是最高的，只是接近最高的性能。要达到最好的性能，需要建立一颗最优二叉树，但是最优二叉树的建立和维护需要大量的操作，因此用平衡 二叉树就比较好。同时，平衡二叉树多用于内存结构对象中，因此维护他的开销相对较小。

②为什么使用B+树呢？

虽然二叉查找树和平衡二叉树都能够实现较快的数据查找，但是，由于数据库的内容是存在于磁盘上，而磁盘IO与内存IO相比，比内存IO慢了10^5～10^6倍，为了减少磁盘IO，提高检索速度，因而才用了B+树这种数据结构。换言之，B+树就是为磁盘或其他直接存取辅助设备而设计的一种多路查找树，是多叉树。

③什么是B+树，其特性是什么

B+树的概念还是过于复杂，直接上图比较合适，来一张维基百科上的截图：

从上面可以看出，所有记录的节点都在叶节点中，并且是顺序存放的，如果我们从最左边的节点开始遍历，可以得到的所有键值的顺序是：1、2、3、4、5、6、7。

在B+树中，所有记录节点都是按照键值的大小顺序存放在同一层的叶节点中，各个叶子节点通过指针进行连接。由于一个节点中存放了多条的数据，那么检索的时候，进行的磁盘IO次数将会少掉很多。这是用b+树而不用二叉树的原因。

在B+树插入的时候，为了保持平衡，对于新插入的键值可能需要做大量的拆分页操作，而B+树主要用于磁盘，因此页的拆分意味着磁盘操作，因此应该在可能的情况下尽量减少页的拆分。因此，B+树提供了旋转的功能。至于旋转和删除等内容，过于复杂，这篇笔记先不做记录。只是了解使用B+树的原因以及B+树的特性。

关于索引

InnoDB存储引擎使用聚集索引，实际的数据行和相关键值保存在一块。因而，在InnoDB中要使用索引访问数据始终需要两次查找，而不是一次。因为索引叶子节点中存储的不是行的物理位置，而是主键的值。即：二次索引-->主键-->数据的叶子-->通过数据叶字节点中的page directory找到数据行。

因为每一张InnoDB的表都会有一个主键索引，但是如果没有显式指定怎么办？如果没有手工去指定主键索引的话，那么，InnoDB引擎会指派一个unique的列作为主键，如果没有unique的字段的话，那么便会自动生成一个隐含的列作为主键。

所以，在在InnoDB的设计中，应该尽可能的使用一个与业务无关auto_increment的自增主键，而不要去使用uuid之类的随机（无序）的聚集键。同时，由于所有的索引都使用主键的索引，如果主键索引过长，也会使辅助索引相应的变大。

聚集索引的存储并不是物理上的连续，而是逻辑上连续的。一方面，页通过双向链表连接，页按照主键的顺序排列；另一方面，每个页中的记录也是通过双向链表进行维护，物理存储上可以同样不按照主键存储。

对于目前的MySQL来说，所有的对于索引的添加或者删除操作，MySQL数据库都是要先创建一张新的临时表，然后再把数据导入临时表，再删除原来的表，然后再把临时表命名为原来的表。所以，如果一张表中数据太多的话，那么后期添加删除索引需要花费很长的时间，因而最好在数据库设计初期便设计好索引。

还有，虽然InnoDB存储引擎从版本innoDB Plugin开始，支持一种称为快速索引创建的方法，但是这种方法只限定于辅助索引，对于主键的创建和删除还是需要重建一张表。