题解P4474 王者之剑

双倍经验

简要题意

给你一个 \(n\times m\) 的网格，数字在格子里，你需要取出一些格子，使得任意两个格子之间没有公共边，输出格子中的数字和的最大值。

\(1 \le n,m \le 100\)

思路

如果我们能把公共边的关系刻画成一个二分图，那么就是在求二分图最大独立集。

首先我们将有公共边的两个点连边，但是如果都连上就不是二分图了。这时候我们搬出二分图建模的基本思路——黑白染色！

我们可以对网格黑白染色（就像国际象棋棋盘那样），对白色的点，连向跟它有公共边的点。可以证明，这样每一条边都是白色连向黑色，满足二分图定义。

最后我们建一个超级源点 \(S\)，连向白点，建一个超级汇点 \(T\)，所有黑点连向它。跑最大流，这样得到的是二分图最大匹配（二分图最小路径点覆盖），然后用二分图点数减去它就好了。

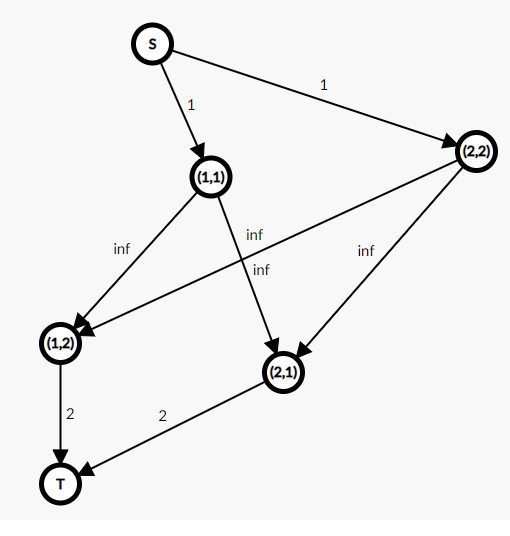
最后附上样例建立的图：

代码

#include<bits/stdc++.h>
#define l(i,j) ((i-1)*m+j)
#define int long long
using namespace std;
int n,m,s,t;

namespace MaxFlow{
	struct edge{
		int from,to,val;
	}e[200001];int head[200001],cur[200001],siz=1;
	void add(int x,int y,int z){
		e[++siz].to=y,e[siz].val=z;
		e[siz].from=head[x],head[x]=siz;
	}
	void addedge(int x,int y,int z){
		add(x,y,z);add(y,x,0);
	}
	int gap[200001];
	bool bfs(){
		memset(gap,0,sizeof(gap));
		fill(gap+1,gap+1+n,0);
		queue<int> q;
		q.push(s);
		gap[s]=1;
		while(!q.empty()){
			int now=q.front();
			q.pop();
			for(int i=head[now];i;i=e[i].from){
				int u=e[i].to;
				if(e[i].val&&!gap[u]){
					gap[u]=gap[now]+1;
					q.push(u);
				}
			}
		}
		return (gap[t]);
	}
	int dfs(int now,int val){
		if(now==t) return val;
		for(int &i=cur[now];i;i=e[i].from){
			int u=e[i].to;
			if(e[i].val&&gap[now]+1==gap[u]){
				int F=dfs(u,min(e[i].val,val));
				if(F){
					e[i].val-=F;
					e[i^1].val+=F;
					return F;
				}
			}
		}
		return 0;
	}
	int dinic(){
		int ret=0;
		while(bfs()){
			copy(head,head+1+n,cur);
			int F=0;
			while(F=dfs(s,10000000000000)){
				ret+=F;
			}
		}
		return ret;
	}
}

int sum;

const int delta[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
signed main(){
	cin>>n>>m;
	s=0,t=m*n+1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			int w;
			cin>>w;
			sum+=w;
			if((i+j)%2){
				MaxFlow::addedge(l(i,j),t,w);
			}
			else{
				MaxFlow::addedge(s,l(i,j),w);
				for(int k=0;k<=3;k++){
					int x=i+delta[k][0],y=j+delta[k][1];
					if((x>=1&&x<=n)&&(y>=1&&y<=m)){
						MaxFlow::addedge(l(i,j),l(x,y),LLONG_MAX);
					}
				}
			}
		}
	}
	n=t;
	cout<<sum-MaxFlow::dinic()<<'\n';
	return 0;
}