支持向量机SVM（一）：基本概念、目标函数的推导

本文旨在介绍支持向量机（SVM）的基本概念并解释SVM中的一个关键问题：

为什么SVM目标函数中的函数间隔取１？

一、分类问题

给定N个分属两类的样本，给出一个决策边界使得边界一侧只含一种样本（如下图）

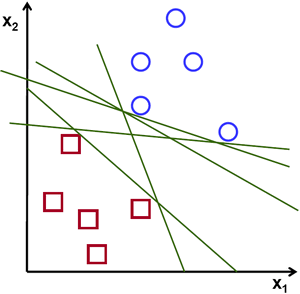
从直观上讲，两种样本集被分开的“间隔”越大表示分类效果越好，如下图中，边界2的效果显然是最好的

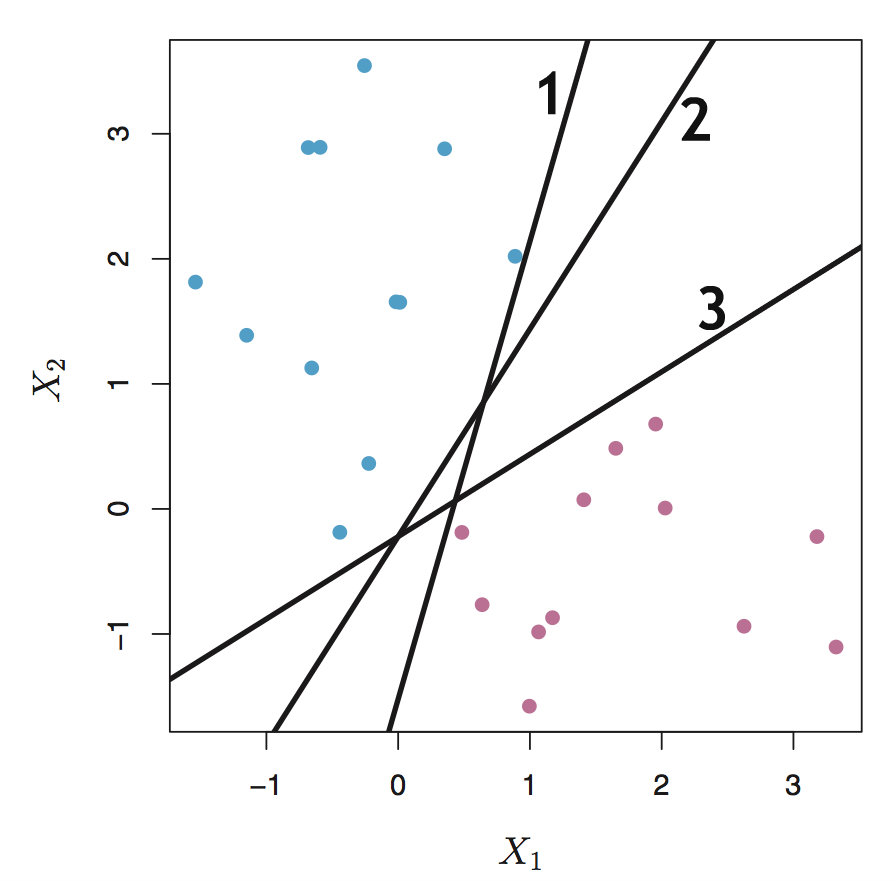
传统的方法来计算间隔时，一般考虑所有样本点，比如可以使用样本集中所有样本点到决策边界的距离和来作为这个样本集到决策边界的距离。由于考虑了所有样本，因此这么做的一个缺点在于对离群值（outlier）十分敏感

我们发现确定决策边界的过程中，最重要的点是两个样本集之间距离靠的最近的那些点，是否可以只利用这些点来给出决策边界呢？SVM就是基于这一点产生的分类技术。

二、SVM相关的数学概念

由于SVM中包含大量数学推导，因此想要完全理解SVM就必须先理解SVM中涉及到的数学概念。

超平面(hyperplane)

上图给出的例子中，样本是二维平面中的点，由(X1, X2)来描述，而决策边界由一条的直线来描述，这条直线将平面分成了两部分。

实际问题中涉及到的样本往往是多维的，比如学生=[学号，姓名，地址，...]，因此需要给出一个更一般的定义。

超平面是n维空间中n-1维的子空间，由方程$a_1 x_1 + \cdots + a_n x_n = b$来确定（其中$a_1 , … , a_n$是不全为零的常数）

超平面将n维空间分成了两部分，比如二维空间$R^2$中，$a_1 x_1 + a_2 x_2= b$表示的直线就是二维空间中的一个超平面，它将平面分为了两部分。

而三维空间$R^3$中，$a_1 x_1 + a_2 x_2 + a_3 x_3= b$表示的平面是三维空间的一个超平面，它将三维空间分为两部分，如下图

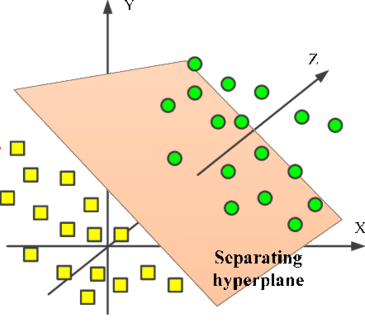
在数据分析领域，一般将d维空间中的样本表示为$(\mathbf{x_i,y_i})，其中\mathbf{x_i} = (x_{i1},x_{i2},...,x_{id})$表示一个d维的向量，$\mathbf{y_i} = \{-1,1\}$表示$\mathbf{x_i}$所属的类别

例如，二维空间中((1, 1), 1)表示点(1,1)属于类别1。

$\mathbf{y_i}$是样本所属的标签，理论上可以取任何值，如{apple, orange}，但为了方便接下来的数学计算，设为{-1,1}

超平面被称为决策边界，一般写成如下的形式：

$w^Tx+b=0$

其中$w=(w_1, ... , w_d)$，$b$是一个常数，称为偏移量

例如，在二维空间中$2x_1+x_2+1=0$就是一个决策边界，其中$w=(2,1)$，$b=1$

注意：

1. 不要把$w$理解为斜率，$b$理解为截距
2. 由于$w,b$可以同比缩放，因此同一个超平面有多种表示方式，如$2x_1+x_2+1=0$和$4x_1+2x_2+2=0$表示同一个超平面

超平面的性质

如果$x_a,x_b$是超平面上$w^Tx+b=0$上的点，则

$w^Tx_a+b=0$

$w^Tx_b+b=0$

相减得到

$w^T(x_a-x_b)=0$

因为$x_a,x_b$是超平面上的点，$x_a-x_b$就是一个平行于超平面的向量。由于点积为零，所以$w$垂直于超平面，即$w$表示超平面$w^Tx+b=0$的一个法向量

点到超平面的距离

$\vec {a}$在$\vec {b}$上的投影公式：

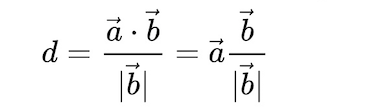
下图中，$A$是超平面上一点，点$P$是超平面外一点

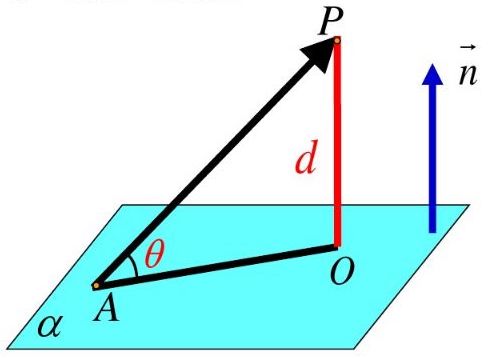
则$P$到超平面$α$的距离为$\vec {AP}$在法向量$\vec {n}$方向上投影的绝对值，即

$d =  \displaystyle \frac{|\vec {AP} · \vec {n}|}{|\vec {n}|}$

因此，设$x$是超平面外一点，$x_0$是超平面内一点，法向量为$w$，则$x$到超平面$w^Tx+b=0$的距离为：

$d = \displaystyle \frac{|w^T(x-x_0)|}{||w||} = \frac{|w^Tx+b|}{||w||}$

这里$||·||$表示L2范数，$||w||_2 = \sqrt{|w_1|^2+|w_1|^2+...+|w_d|^2}$

同时，这里可以看出，如果点$x$在超平面$w^Tx+b=0$的“上方”（$w$指向的那一侧），则$x-x_0$与$w$的夹角$θ∈[0,\displaystyle \frac{\pi}{2})$（图中$\vec {AP}$和$\vec {n}$的夹角），因此$w^Tx+b = w^T(x-x_0) = |w|·|x-x_0|·cosθ > 0$

同理， 如果点$x$在超平面$w^Tx+b=0$的“下方”，$w^Tx+b < 0$

三、 SVM分类器

SVM分类器的目标是给出一个决策边界（超平面）将样本正确地分为两类，且该决策边界拥有最大的边缘

决策边界

首先，我们需要找出正确分类的超平面，即对于所有样本$(\mathbf{x_i,y_i})$，满足$\mathbf{y_i}=1$的$\mathbf{x_i}$都在超平面的一侧，而满足$\mathbf{y_i}=-1$的$\mathbf{x_i}$都在超平面的另一侧

一般来说，我们希望$\mathbf{y_i}=1$的样本都在超平面上方，$\mathbf{y_i}=-1$的样本都在超平面下方

需要注意的是“上方”和“下方”并不是视觉上的超平面上面或下面，而是以超平面的法向量$w$指向的方向为上方，反之为下方

根据之前的计算，我们知道：

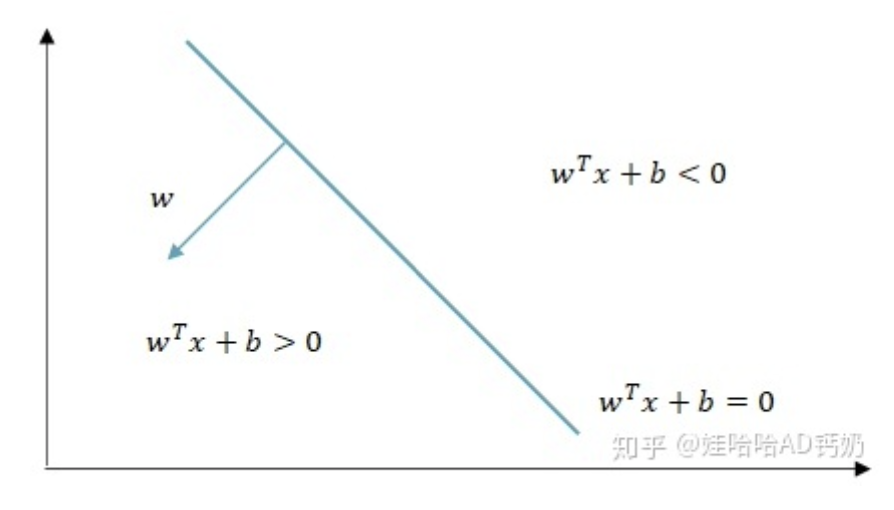
$w^Tx+b > 0$ ⇔ 点$x$在超平面$w^Tx+b=0$的上方

$w^Tx+b < 0$ ⇔ 点$x$在超平面$w^Tx+b=0$的下方

因此，当超平面w^Tx+b正确分类时，对所有样本$(\mathbf{x_i,y_i})$：

$w^Tx_i+b > 0, y_i = 1$

$w^Tx_i+b < 0, y_i = -1$

这时将$y_i$定义为{-1,1}的方便之处就体现出来了，上述约束可以简化为：

$y_i(w^Tx_i+b) >0, ∀i$

函数间隔、几何间隔

点$x_i$到超平面的距离$d = \displaystyle \frac{|w^Tx_i+b|}{||w||}$，我们将其称为$x_i$到超平面的几何间隔γ

当超平面正确分类时，上式也可以写成：$γ = \displaystyle \frac{y_i(w^Tx_i+b)}{||w||}$，同时，我们将$y_i(w^Tx_i+b)$称为$x_i$到超平面的函数间隔γ'

因此，我们得到$γ' = γ · ||w||$

同一个超平面有多种表示方式，如：$w_1^Tx+b_1=0$ 和 $2w_1^Tx+2b_1=0$，因此即使是同一个超平面，$x_i$的函数间隔γ'也和表示超平面的$w,b$有关，

对于一个确定超平面，$x_i$到超平面的几何间隔表示点到超平面的实际距离，这是一个定值，和超平面的表示方式无关

例：样本点$(x_1, y_1)$= ((1, 1), 1)，样本点$(x_2, y_2)$= ((-1, -1), -1)，决策边界$x_{i1}+x_{i2}-1 = 0$，即$w=(1,1), b=-1$，如下图

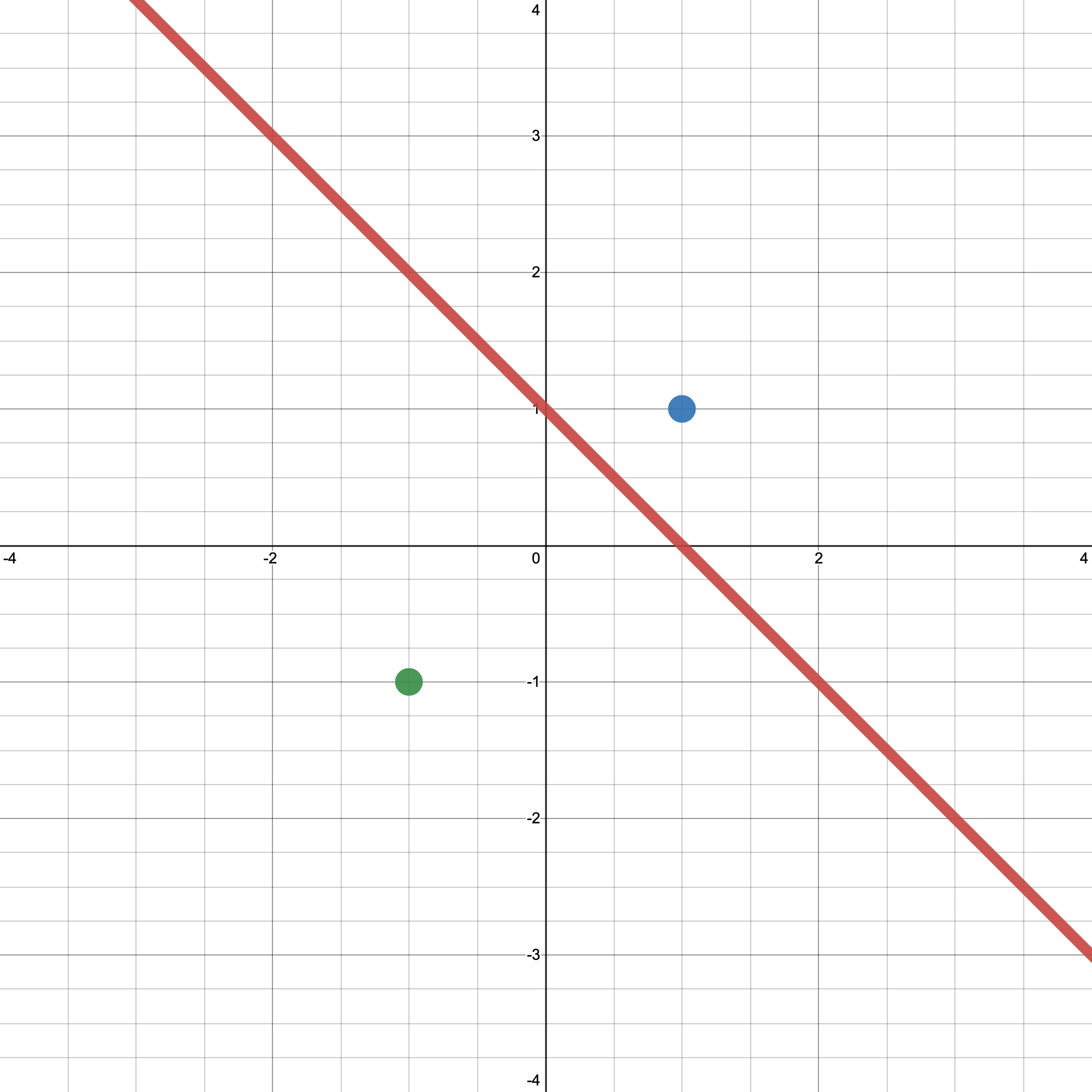
对于$x_1，γ' = y_1(w^T·x_1 + b) =  1 * (1*1 + 1*1 - 1) = 1，γ = \displaystyle \frac{γ'}{\sqrt{1+1}} = \frac{\sqrt{2}}{2}$

对于$x_2，γ' = y_2(w^T·x_2 + b) = -1 * (-1*1 + -1*1 - 1) = 3，γ = \displaystyle \frac{γ'}{\sqrt{1+1}} = \frac{3\sqrt{2}}{2}$

最大边缘