一：01背包问题模型

1 题目：

有一个箱子容量为 V，同时有 n 个物品，每个物品有一个体积（正整数）。

要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入格式

第一行是一个整数 V，表示箱子容量。

第二行是一个整数 n，表示物品数。

接下来 n 行，每行一个正整数（不超过10000），分别表示这 n 个物品的各自体积。

输出格式

一个整数，表示箱子剩余空间。

数据范围

0<V≤200000<V≤20000,
0<n≤300<n≤30

输入样例：

输出样例：

代码：

 1 #include <bits/stdc++.h>

 2 using namespace std;

 3

 4 const int N = 20010;

 5 int dp[N];

 6

 7 int main(){

 8     int V;cin >> V;

 9     int n;cin >> n;

10     for(int i = 1;i <= n;++i){

11         int v;cin >> v;

12         for(int j = V;j >= v;--j)

13             dp[j] = max(dp[j], dp[j - v] + v);

14     }

15     cout << V - dp[V];

16     return 0;

17 }

2 数字组合问题

题目：

给定N个正整数A1,A2,…,ANA1,A2,…,AN，从中选出若干个数，使它们的和为M，求有多少种选择方案。

输入格式

第一行包含两个整数N和M。

第二行包含N个整数，表示A1,A2,…,ANA1,A2,…,AN。

输出格式

包含一个整数，表示可选方案数。

数据范围

1≤N≤1001≤N≤100,
1≤M≤100001≤M≤10000,
1≤Ai≤10001≤Ai≤1000

输入样例：

4 4

1 1 2 2

输出样例：

代码：

 1 #include <iostream>

 2 using namespace std;

 3

 4 const int N = 10010;

 5

 6 int dp[N];

 7 int arr[110];

 8

 9 int main(){

10     int n, m;cin >> n >> m;

11     for(int i = 1;i <= n;++i)cin >> arr[i];

12     dp[0] = 1;

13     for(int i = 1;i <= n;++i)

14         for(int j = m;j >= arr[i];--j)

15             dp[j] = dp[j] + dp[j-arr[i]];

16     cout << dp[m];

17 }

数字组合问题2：

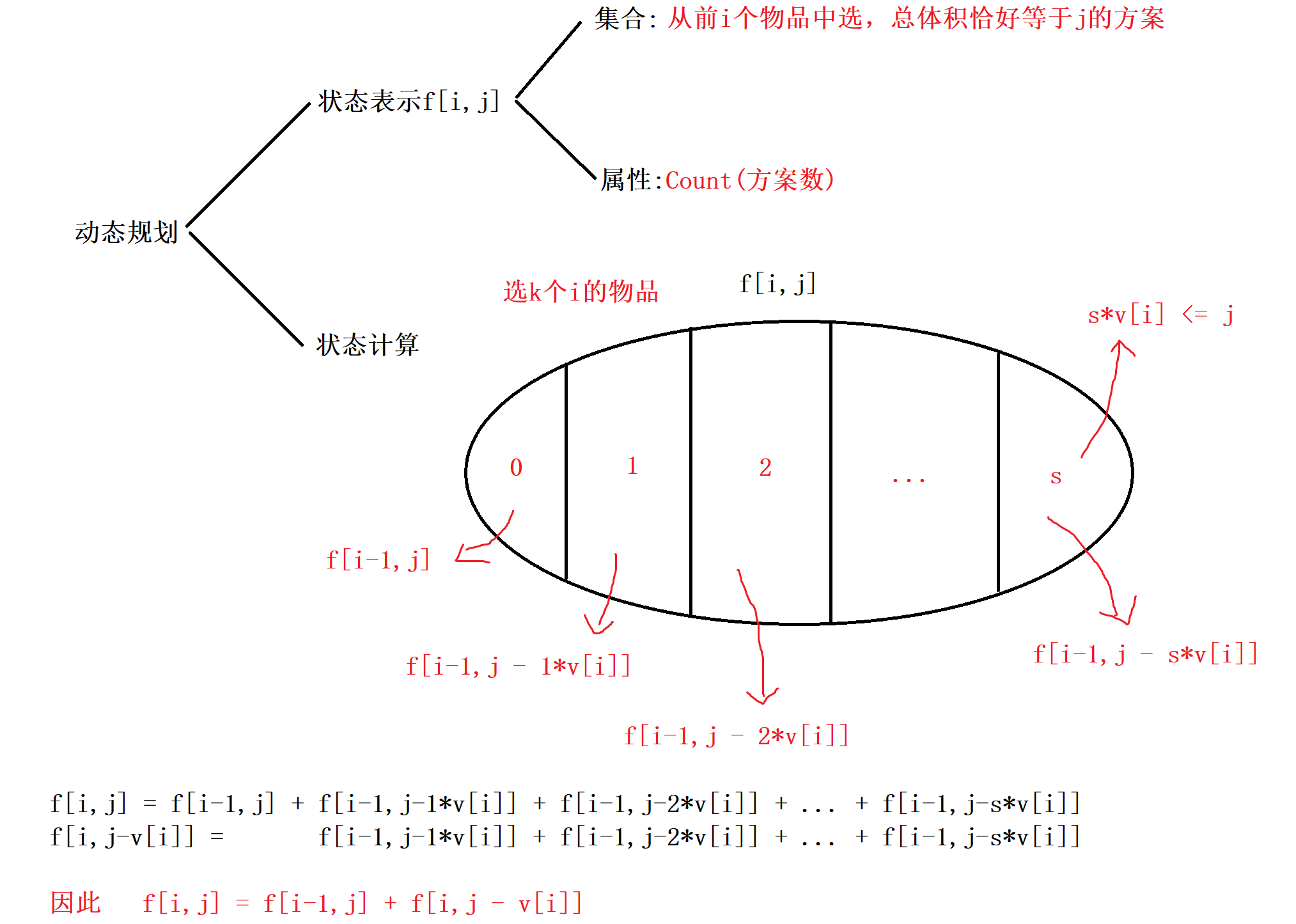
二：完全背包模型：

1：题目：

小明手里有n元钱全部用来买书，书的价格为10元，20元，50元，100元。

问小明有多少种买书方案？（每种书可购买多本）

输入格式

一个整数 n，代表总共钱数。

输出格式

一个整数，代表选择方案种数。

数据范围

0≤n≤10000≤n≤1000

输入样例1：

输出样例1：

输入样例2：

输出样例2：

输入样例3：

输出样例3：

算法分析：

代码：

 1 #include <iostream>

 2

 3 using namespace std;

 4

 5 const int N = 1010;

 6

 7 int n;

 8 int v[4] = {10, 20, 50, 100};

 9 int f[N];

10

11 int main()

12 {

13     cin >> n;

14

15     f[0] = 1;

16     for (int i = 0; i < 4; i ++ )

17         for (int j = v[i]; j <= n; j ++ )

18             f[j] += f[j - v[i]];

19

20     cout << f[n] << endl;

21

22     return 0;

23 }

需要注意的是本题求的是方案数，也就是说手里的钱是必然全部花光的，而求价值的完全背包问题，手里的钱是不一定全部花光的

才用上面的代码定义的dp就是方案数，不会因为这个问题出错

2：稍微有点难度的完全背包问题

题目：

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。

为了方便，我们把货币种数为 n、面额数组为 a[1..n] 的货币系统记作 (n,a)。

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n 个非负整数 t[i] 满足 a[i]× t[i] 的和为 x。

然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额 x 不能被该货币系统表示出。

例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。

他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a) 等价，且 m 尽可能的小。

他们希望你来协助完成这个艰巨的任务：找到最小的 m。

输入格式

输入文件的第一行包含一个整数 T，表示数据的组数。

接下来按照如下格式分别给出T组数据。

每组数据的第一行包含一个正整数 n。

接下来一行包含 n 个由空格隔开的正整数 a[i]。

输出格式

输出文件共有T行，对于每组数据，输出一行一个正整数，表示所有与 (n,a) 等价的货币系统 (m,b) 中，最小的 m。

数据范围

1≤n≤1001≤n≤100,
1≤a[i]≤250001≤a[i]≤25000,
1≤T≤201≤T≤20

输入样例：

2

4

3 19 10 6

5

11 29 13 19 17

输出样例：

2

5

思路分析
1：通过本题明白给定一个数组如何找出数组中除了他自己以外不可以被其他元素（其他元素可以选取的个数是无限的）通过相加的方式得到的数就可以，我们可以想到和完全背包问题相类似，所以我们可以借鉴一下完全背包的思路
2：dp[i] 表示元素i可以被数组中的元素表示出来的的方案数，如果等于1那么可知改元素符合条件，计算求方案数才用和上面的题一样的方法
3：不可以被其他元素表示出来得到的数，一定可以通过某些相加的方式把其他元素表示出来

代码：

 1 #include <bits/stdc++.h>

 2 using namespace std;

 3

 4 const int N = 25010;

 5

 6 int dp[N];

 7 int arr[N];

 8

 9 int main(){

10     int T;cin >> T;

11     while(T --){

12         int n;cin >> n;

13         for(int i = 1;i <= n;++i) cin >> arr[i];

14

15         sort(arr, arr+1+n);

16

17         int m = arr[n];

18         memset(dp, 0, sizeof dp);

19         dp[0] = 1;// 组成0的方案数是1

20

21         for(int i = 1;i <= n;++i){

22             for(int j = arr[i];j <= m;++j)

23                 dp[j] = dp[j] + dp[j-arr[i]];

24         }

25

26         int ans = 0;

27         for(int i = 1;i <= n;++i)

28             if(dp[arr[i]] == 1) ++ans;

29         cout << ans << endl;

30     }

31     return 0;

32 }

dp-背包模型的更多相关文章

dp表模型-如何写出for循环动态规划
题目很肤浅.. 但是这件事我们要做.. 那么有一种方法叫做刷表法.. 当你发现这个问题具有最优子结构,重叠子问题时那么这是一个dp问题是使用本方法的前提画出该dp状态所对应的矩阵画出转移关系线. ...
NYOJ16|嵌套矩形|DP|DAG模型|记忆化搜索
矩形嵌套时间限制:3000 ms | 内存限制:65535 KB 难度:4 描述有n个矩形,每个矩形可以用a,b来描述,表示长和宽.矩形X(a,b)可以嵌套在矩形Y(c,d)中当且仅当a& ...
【bzoj1688】[USACO2005 Open]Disease Manangement 疾病管理状态压缩dp+背包dp
题目描述 Alas! A set of D (1 <= D <= 15) diseases (numbered 1..D) is running through the farm. Far ...
括号序列的dp问题模型
括号序列的dp问题模型 Codeforces314E ◦给定一个长度为n的仅包含左括号和问号的字符串,将问号变成左括号或右括号使得该括号序列合法,求方案总数. ◦例如(())与()()都是合法的括号 ...
URAL_1018 Binary Apple Tree 树形DP+背包
这个题目给定一棵树,以及树的每个树枝的苹果数量,要求在保留K个树枝的情况下最多能保留多少个苹果一看就觉得是个树形DP,然后想出 dp[i][j]来表示第i个节点保留j个树枝的最大苹果数,但是在树形过 ...
hdu1561 The more, The Better (树形dp+背包)
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=1561 思路:树形dp+01背包 //看注释可以懂用vector建树更简单. 代码: #i ...
HDU 5234 DP背包
题意:给一个n*m的矩阵,每个点是一个蛋糕的的重量,然后小明只能向右,向下走,求在不超过K千克的情况下,小明最终能吃得最大重量的蛋糕. 思路:类似背包DP: 状态转移方程:dp[i][j][k]--- ...
dp常见模型
1.背包问题.0/1背包.完全背包.多重背包.分组背包.依赖背包. 2.子序列.最长非上升/下降子序列.最长先上升再下降子序列.最长公共子序列.最大连续子区间和. 3.最大子矩阵. 4.区间dp. 5 ...
HDU4276 The Ghost Blows Light（树形DP+背包）
题目大概说一棵n个结点树,每个结点都有宝藏,走过每条边要花一定的时间,现在要在t时间内从结点1出发走到结点n,问能获得最多的宝藏是多少. 放了几天的题,今天拿出来集中精力去想,还是想出来了. 首先,树 ...
HDU 4003 (树形DP+背包)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=4003 题目大意:有K个机器人,走完树上的全部路径,每条路径有个消费.对于一个点,机器人可以出去再回来 ...

随机推荐

js与java encodeURI 进行编码与解码
JS escape()使用转义序列替换某些字符来对字符串进行编码 JavaScript 中国编码后 JavaScript %u4E2D%u56FD unescape()对使用 encodeUR ...
HTML：<input type="text"> 输入数字时的验证！（在提交时验证）
 < ...
《A Neural Algorithm of Artistic Style》理解
在美术中,特别是绘画,人类掌握了通过在图像的内容和风格间建立复杂的相互作用从而创造独特的视觉体验的技巧.到目前为止,这个过程的算法基础是未知的,也没有现存的人工系统拥有这样的能力.然而在视觉感知的其他 ...
C++ 模板和泛型编程（掌握Vector等容器的使用）
1. 泛型泛型在我的理解里,就是可以泛化到多种基本的数据类型,例如整数.浮点数.字符和布尔类型以及自己定义的结构体.而容器就是提供能够填充任意类型的数据的数据结构.例如vector就很类似于pyth ...
Throwable类中3个异常处理的方法和finally代码块
/* Throwable类中定义了3个异常处理的方法 String getMessage() 返回此 throwable 的简短描述. String toString() 返回此 throwable ...
C++指针和结构体基础知识
学习C++首先要回忆起C语言当中的指针和结构体知识,本文作者将通过一段代码来总结指针和结构体基础知识:指针是一个变量,其值为另一个变量的地址,即,内存位置的直接地址.就像其他变量或常量一样,您必须在使 ...
【实操填坑】在树莓派上编译 EtherCAT IgH Master 主站程序
官网下载地址:https://etherlab.org/download/ethercat/ (可list查看文件列表)https://etherlab.org/download/ethercat/ ...
linux 学习 mysql安装到连接
在Centos7.6 上安装mysql ps:一般mysql安装后会在/var/log/下面生成一个mysqld.log文件,如果遇到启动不了或者其他问题,基本都可以在这个log文件里面找到错误原因 ...
python 上下文管理(with、contextmanager)
简介 python中存在这么一个非常好用的东西,能够帮助我们更好的管理上下文,这种东西就成为上下文管理器,例如我们最常见的with open,在读取文件时可以很方便的进行文件描述符和文件对象的打开和关 ...
Linux学习系列--如何在Linux中进行文件的管理
文件在常见的Linux的文件系统中,经常使用能了解到的文件管理系统是分为多个文件夹进行管理的. 如何查看文件路径 pwd ,在文件目录中,会有一个点(.)代表的是当前目录,两个点(..)代表的是当前 ...

dp-背包模型

一：01背包问题模型

1 题目：

输入格式

输出格式

数据范围

输入样例：

输出样例：

代码：

2 数字组合问题

题目：

输入格式

输出格式

数据范围

输入样例：

输出样例：

代码：

数字组合问题2：

二：完全背包模型：

1：题目：

输入格式

输出格式

数据范围

输入样例1：

输出样例1：

输入样例2：

输出样例2：

输入样例3：

输出样例3：

算法分析：

代码：

需要注意的是本题求的是方案数，也就是说手里的钱是必然全部花光的，而求价值的完全背包问题，手里的钱是不一定全部花光的

才用上面的代码定义的dp就是方案数，不会因为这个问题出错

2：稍微有点难度的完全背包问题

输入格式

输出格式

数据范围

输入样例：

输出样例：

dp-背包模型的更多相关文章

随机推荐

热门专题