ACM组合计数入门

1 排列组合

1.1 排列

\[A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!}
\]

• 定义：从 n 个中选择 m 个组成有序数列，其中不同数列的数量。
• 解释：从 n 个中选一个，有 n 种选法，再选第二个，从 n-1 个中选，有 n-1 种选法，以此类推，根据组合数学的乘法原理所以公式是\(n(n-1)(n-2)...(n-m+1)\)。

1.2 组合

\[C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}
\]

• 定义：从 n 个 中选择 m 个组成集合其中，不同的集合的数量。
• 解释：在排列中去掉选择重复元素的情况就是组合了，比如 {1，2，3}、{2，3，1} 相同，所以公式是$ \frac{A_n^m}{A_mm}$,即从 n 个 中选出 m 个，排列完除去 m 个全排列的数量。
• 另外：\(C_n^m\) 还有一种写法是： \(\binom{n}{m}\)，读作 n 选 m。
• 推论：
  1. \(\binom{n}{m}+\binom{n}{m-1}=\binom{m+1}{i}\) ，(又叫帕斯卡法则)，带入公式约分后易证。

二项式定理

\[(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^{n-i}b^i
\]

• 证明：

\[当 n=1 时，a+b= \sum_{i=0}^1\binom{1}{i}a^{1-i}b^i=\binom{1}{0}a^1b^0+\binom{1}{1}a^0b^1=a+b ,公式成立
\]

\[假设n=m 时公式成立，设n=m+1，则有：
\]

\[(a+b)^{m+1}=a(a+b)^m+b(a+b)^m
\]

\[= a\sum_{i=0}^m\binom{m}{i}a^{m-i}b^i+b\sum_{j=0}^m\binom{m}{j}a^{m-j}b^j
\]

\[= \sum_{i=0}^m\binom{m}{i}a^{m+1-i}b^i+\sum_{j=0}^m\binom{m}{j}a^{m-j}b^{j+1},提出当i=0时和当j=m时的项
\]

\[= a^{m+1}+ \sum_{i=1}^m\binom{m}{i}a^{m+1-i}b^i +b^{m+1} +\sum_{j=0}^{m-1}\binom{m}{j}a^{m-j}b^{j+1} ，令j=i-1
\]

\[= a^{m+1} +b^{m+1}+ \sum_{i=1}^m\binom{m}{i}a^{m+1-i}b^i+\sum_{i=1}^{m}\binom{m}{i-1}a^{m+1-j}b^i
\]

\[=a^{m+1} +b^{m+1}+ \sum_{i=1}^m\Bigg[\binom{m}{i}+\binom{m}{i-1}\Bigg]a^{m+1-i}b^i,根据：\binom{n}{m}+\binom{n}{m-1}=\binom{m+1}{i}
\]

\[=a^{m+1} +b^{m+1}+ \sum_{i=1}^m\binom{m+1}{i}a^{m+1-i}b^i
\]

\[= \sum_{i=0}^{m+1}\binom{m+1}{i}a^{m+1-i}b^i
\]

• 推论：
  • $ C_n^0+C_n1+C_n^2\cdots+C_nn=(1+1)ⁿ⁼²n $
  • $ C_n^0-C_n1+C_n^2-C_n3\cdots +C_n^n=(1-1)n=(0)^n$

Lucas 定理

若 p 是质数，则对于任意整数 $ 1 \le m \le n $ 有：

\[\binom{n}{m} \equiv \binom{n ~ mod ~ p}{m ~ mod ~ p}\binom{n/p}{m/p} (mod~p)
\]

证明较难，需要用到生成函数的知识，有兴趣的可以看看。别问我，我也不会。

使用这个公式就可以对较为麻烦的组合数进行取模。

鸽巢定理

• 定义：将 n+1 个物体，划分为 n 组，那么有至少一组有两个（或以上）的物体。

• 推广：将 n 个物体，划分为 k 组，那么至少存在一个分组，含有大于或等于 \(\lceil \frac{n}{k} \rceil\) 个物品。

• 例题：给你n个正整数\(A=\{a_1,a_2...a_n\}\)，和一个正整数 c，问，是否能找到一个 A 的子集 B，B 中元素的和是 c 的倍数，如果能则输出他们的编号。\(1 \le c \le n \le 10^5 ,1 \le a_i \le 10^5\)。

  • 解法：设 A 的前缀和为 $ sum_i $ ，
  \[若有 sum_l \equiv sum_r~(mod~c)
  \]
  \[即 sum_l -sum_r\equiv0 ~(mod~c)
  \]
  \[那么 \sum_{i=l+1}^ra_i\equiv0 ~(mod~c)
  \]
  \[所以\sum_{i=l+1}^ra_i 即为解
  \]
  \[前缀和的个数为 n ,模 c 的情况下去除为0的情况，总共有 c-1 种情况，n>c-1
  \]
  \[根据鸽巢定理 一定有 sum_l \equiv sum_r~(mod~c)
  \]
  \[综上所述：该题恒有解，解为\{ a_{l+1},a_{l+2},\cdots ,a_r |sum_l \equiv sum_r~(mod~c) \}
  \]

容斥定理

• 定义：$$ 设有 _n 个集合 _{S_i} , _{|S_i|} 表示 _{S_i} 的大小，有：$$

  \[\left| \bigcup_{i=1}^nS_i \right|=\sum_{i=1}^{n}|S_i|-\sum_{1 \le i < j \le n}|S_i\cap S_j|+\sum_{1 \le i < j <k \le n}|S_i\cap S_j\cap S_k|- \cdots
  \]
  \[+(-1)^{m-1}\sum_{a_i<a_{i+1}}\left| \bigcap_{i=1}^mS_{a_i} \right|+ \cdots + (-1)^{n-1}\left| \bigcap_{i=1}^nS_i \right|
  \]

  公式看起来好复杂、好吓人，但实际上是个很简单的定理。
  
  如下图有集合A、B、C：
  
  

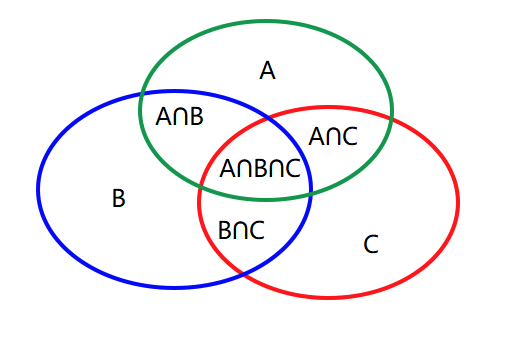
  显然有：

  \[|A\cup B\cup C|= |A|+|B|+|C|-|A\cap B|-|A\cap C| -|B\cap C|+|A\cap B\cap C|
  \]

  把这个问题推广到一般情况，就是我们熟知的容斥原理。

• 证明：

  \[设~T_i~为元素~a_i~在集合~S_1,S_2,\cdots ,S_n~ 中出现的次数
  \]
  \[因为容斥定理公式相当于~1-n~的所有组合情况，也就是组合数的全集，此时我们再在全集中选择包含元素~a_i~的组合
  \]
  \[所以在容斥定理公式，中元素~a_i~出现的次数为：
  \]
  \[\sum_{j=1}^{T_i} (-1)^{i-1}\binom{T_i}{j}
  \]
  \[根据二项式定理:(1-1)^n=\sum_{i=0}^{n}\binom{n}{i}(-1)^{i} ,有：
  \]
  \[0= 1-\sum_{i=1}^{n} (-1)^{i-1}\binom{n}{i}
  \]
  \[即：\sum_{i=1}^{n} (-1)^{i-1}\binom{n}{i}=1
  \]
  \[所以 \sum_{j=1}^{T_i} (-1)^{i-1}\binom{T_i}{j} =1，即元素~a_i~出现的次数为~1
  \]
  \[也就是说在容斥定理公式任意元素出现的次数都为~1 ，那么合并起来就是并集。
  \]

• 例题：区间互质问题，两个区间中互质对的个数，两区间范围不超过\(10^6\)。
  
  在考虑这个问题之前我们先考虑它的一个子问题，一个数 \(x\) 与一个区间 \([l,r]\) 的互质问题。处理这个问题，最简单的方法肯定是遍历区间然后用 \(gcd\) ，复杂度为\(O(NlogN)\)，n 为区间长度，加上另外一个区间那\(O(N^2logN)\),显然太慢，这时我们可以逆向思维，转换问题，我们可以考虑求不互质的个数，然后再用全部个数减去不互质的个数。不互质也就是说，有公共的因子，如果把问题转换成求同有某个因子的数量，那就好处理，比如如果计算都有因子 2，即 2 的倍数的数量，只要讲区间数除2就好，也就是说只要 \(O(1)\) 的复杂度就可以算出区间中有某个因数的数的个数，也就是说我们可以先对数 \(x\) 进行因数分解，得到 $ m $ 个因数 $ a_1,a_2,\cdots ,a_m $，对于某个因数我们可以求出区间 \([l,r]\) 中,包含因数 $ a_i $ 的数量 $ b_i $,如有一因子为 \(a_1=3\) ，区间为 $ [5,18] $ ,那么对应的 $ b_1=\lfloor \frac{18-5+1}{3} \rfloor=5,即有{6,9,12,15,18}这 5 个数，有$ $b
  
  _i=\lfloor \frac{r-l+1}{a_i} \rfloor $
  
  看起来我们好像把所有的 $ b_i $ 加起来就可以解决这个问题了，但实际上如果直接把 $ b_i $ 加起来，最后答案会多出很多，比如同时有 2 和 3 作为因子的数，如果我们直接加，那 6 的倍数就被多算，并且如果有 2 和 6 为因子，那 6 也一定是一个因子，那就更加麻烦了。为了解决这个问题，我们还需要将问题再度分解，我们将 $ x $ 拆分成质因子 $ p_1,p_2,\cdots,p_k $，设 \(k\) 份集合\(S_1,S_2,\cdots ,S_k\) , \(S_i\) 表示在区间中包含因子 \(p_i\) 的数所构成的集合。根据容斥定理此时就有我们要求的值即：

  \[\left| \bigcup_{i=1}^kS_i \right| =\sum_{j=1}^k \left((-1)^{j-1}\sum_{a_i<a_{i+1}}\left| \bigcap_{i=1}^jS_{a_i} \right| \right)
  \]
  \[设 \sum_{a_i<a_{i+1}}\left| \bigcap_{i=1}^jS_{a_i} \right| 为 A_j
  \]
  \[有：\left| \bigcup_{i=1}^kS_i \right| =\sum_{j=1}^k (-1)^{j-1} A_j
  \]
  \[设 函数~f(x),表示~x~质因子的数量
  \]
  \[有：A_j=\sum_{f(a_i)=j} b_i
  \]

  这里的 \(A_j\) 的实际意义是区间中包含质因子大于等于 \(j\) 的数的数量，所以我们对每一个因子求出它的质因子的数对应将它的 \(b_i\) 累加到 \(A_j\) 中就可以求出 \(A_j\) 的值。换个角度说，因子是质因子的所有非空组合，我们求的 \(b_i\) 即是在这种组合下有多少区间有多少对应的数，比如将所有两两组合的因子的 \(b_i\) 值累加，那我们就可以求出区间有多少包含两个及两个以上的质因子的数的数量了，然后通过容斥定理去重，就可以得出解。
  
  那这个方法的复杂度如何呢？我们先观察该方法的步骤

  1. 对 \(x\) 分解质因数
  2. 对质因数进行全组合，然后计算对应的 \(b_i\) 值累加到 \(A_j\) 上。
  3. 计算容斥定理公式，得出不互质对的数量。
  4. 将区间范围减去上面求出的量，得出解。

  步骤 1 使用 Pollard-rho 算法分解质因数，复杂度为 \(O(n^{\frac{1}{4}})\)，步骤 2 对质因数进行全组合，假设 \(x\) 为 $ p_1^{n_1}p_2{n_2}\cdots p_n^{n_k} $ 总共有 $ (n_1+1)(n_2+1)\cdots (n_k+1) -1$ 种情况,减 1 是因为 1 虽然是因子，但是不算 ，k为质因子的种类数量，考虑到\(1081080=2×2×2×3×3×3×5×7×11×13，256\)，并且计算对应的 \(b_i\) 值的复杂度为 \(O(1)\)，通过查表（http://wwwhomes.uni-bielefeld.de/achim/highly.txt ），发现它的增长低于 \(O(n^{\frac{1}{4}})\) 但 $ 10^6 $ 以内大于 \(O(n^{\frac{1}{4}})\)，在。步骤 3 计算交错加减，复杂度 $ O(k) $ 。步骤 4 复杂度 \(O(1)\)。综上所述，在数据范围为 $ 10^6 $ 时，最坏的情况需要百位的运算次数，在普适的范围内复杂度可以看作\(O(n^{\frac{1}{4}})\)。

  我们在\(O(n^{\frac{1}{4}})\)的复杂度内求出了一个数对于一个区间的互质对，那一个区间和一个区间的互质对一样，对区间中每一个数求解就好，复杂度为\(O(n^{\frac{5}{4}})\)。

另外

组合数还有很多内容比如：

• 卡特兰数
• 斯特林数
• 贝尔数
• 伯努利数
• 多重集的排列组合
• 不相邻排列
• 错位排列
• 圆排列

这些都是一些经典计数模型，可以不用会证明或者推导，但是要知道他们能解决什么类型的问题，他们的模型是什么。

如果对组合计数很感兴趣，可以学下生成函数（母函数）