主成分分析PCA学习一条龙

转自：https://yoyoyohamapi.gitbooks.io/mit-ml/content/%E7%89%B9%E5%BE%81%E9%99%8D%E7%BB%B4/articles/PCA.html

https://www.jianshu.com/p/162bb4ea1b7f

1.有什么功能？

进行数据降维，从n个特征里选出k个最具有代表性的，使数据损失降到最小，尽可能保有原来的数据特征。

假设需要从n维降到k维，那么需要找出k个n维向量，将原有的数据投影到k个n维向量构成的k维空间，并保证投影误差足够小。

比如下图，就找到了2个3维向量，构成了一个二维平面，可将3维特征进行投影。

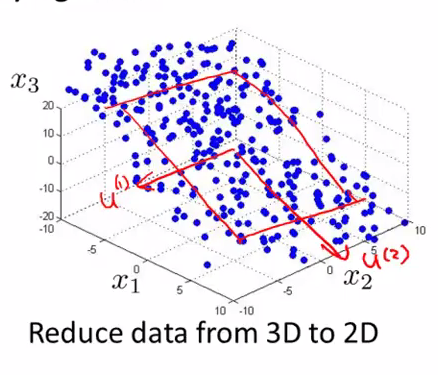
2.算法的步骤

1.先进行标准化，使数据的差值不那么大：

//标准差你应该记得怎么算的吧，就是根号下的方差。

2.计算协方差矩阵Σ：

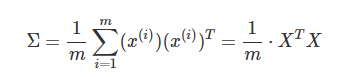
3.通过奇异值分解（SVD），求取 ΣΣ 的特征向量（eigenvectors）：

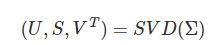
4.从 U中取出前 k个左奇异向量，构成一个约减矩阵 UreduceUreduce:

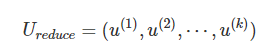
5.计算新的特征向量：z(i):

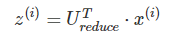
//↑以上过程我都不明白，跟我看的另外一个教程不一样啊。

3.算法的步骤

转自：https://blog.csdn.net/huangfei711/article/details/78663474

PCA 操作流程

去平均值，即每一位特征减去各自的平均值（当然，为避免量纲以及数据数量级差异带来的影响，先标准化是必要的）
计算协方差矩阵
计算协方差矩阵的特征值与特征向量
对特征值从大到小排序
保留最大的个特征向量
将数据转换到个特征向量构建的新空间中

假设二维数据为 data:

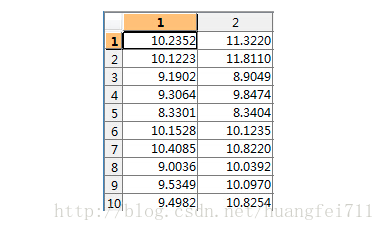
取均值：

去均值矩阵：

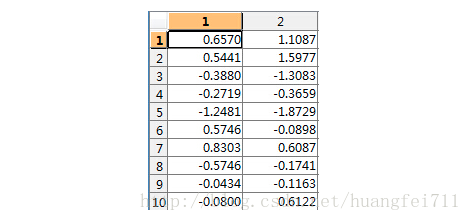
计算其协方差矩阵：

计算协方差矩阵的特征值和特征向量：

特征值为：

特征向量为：

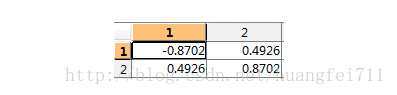
对特征值进行排序（只有两个特征）
选择最大的特征值对应的特征向量：

转换到新的空间

这就完成了PCA的降维操作。

更深入的理解：2019-3-18更——

http://blog.codinglabs.org/articles/pca-tutorial.html

4.对以上的说明

2018-12-21更——

1.如何计算协方差矩阵？

有推导过程：

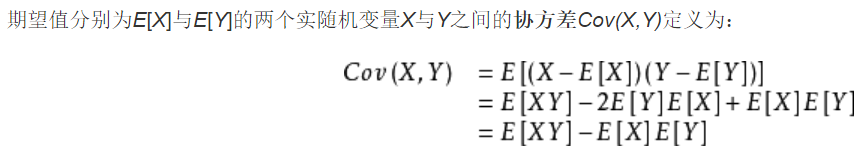
那么其实用第一个和最后一个得到的结果是一样的，实验如下：

> i<-c(,,,)

> j<-c(,,,)

> mean(i*j)-mean(i)*mean(j)

[] 94.875

> mean((i-mean(i))*(j-mean(j)))

[] 94.875

转自：https://wenku.baidu.com/view/e41e9f4cbed5b9f3f90f1c55.html

2.如何计算特征值？

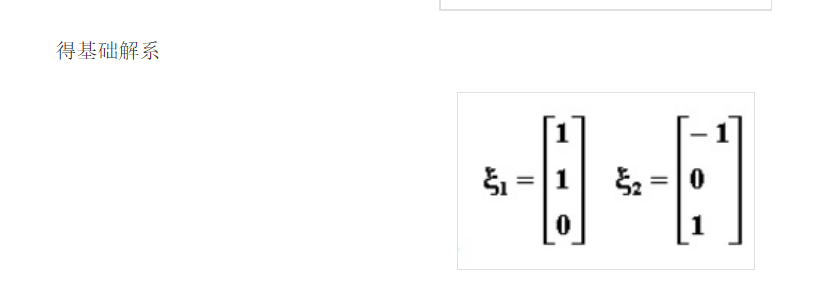
2020-2-25更新——————————

https://www.jianshu.com/p/162bb4ea1b7f 这个讲的不错

#为什么我还要更新呢，因为我发现我对PCA的原理还并不了解，不怎么清楚，每次提到PCA我还是很模糊的。(我的理解就是在坐标系中，主成分代表的线和其他的都很近且平行之类的。)

它的原理就是将很多互相之间有相关的特征降维，使新的特征之间尽可能地不相关，用更少的特征来表示原来的信息。

比如每一个主成分如下：

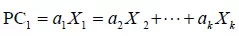
是观测变量的线性组合。

选出的主成分就是和其他特征高度相关的新特征，这样才具有代表性。

https://towardsdatascience.com/pca-using-python-scikit-learn-e653f8989e60

这个是一个PCApython教程，我今天应该没有时间看，但是会学习的。

https://www.cnblogs.com/pinard/p/6239403.html 这个要看，因为有提到了一句，PCA是基于投影方差最大，我不理解。操，白看。但我目前还在看CCA，所以这个方面先不花太多时间了。