XJOI 3605 考完吃糖(DAG图dfs)

题目描述：

期末考试考完了，分数也出来了，大家准备吃糖庆祝一下，为了鼓励同学们下学期能取得更好的成绩，司马红豆同学让n个同学站成一排，如果某个同学的分数比相邻的一个同学要高，那么他得到的糖果就会比这个分数较低的相邻的同学多，每个人至少能得到一个糖果。现在司马红豆想要知道最少需要多少个糖果能完成分糖任务。

输入格式：

第一行输入一个整数n, (1≤n≤100000)

第二行输入n 个整数，依次表示排成一排后每位同学的分数ai, (1≤ai≤1000)。

输出格式：

输出一个整数，表示最少需要的糖果数量

样例输入1：

3
1 0 2

样例输出1：

5

样例输入2：

3
1 2 2

样例输出2：

4

题解：这题乍一看就感觉要抽象成图论模型
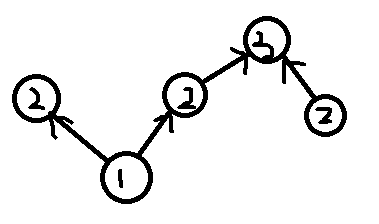
将小的数建一条指向大的数的边，建完边你会得到这样的东西

显然一个点所需要的最大糖数是所有入度为零的点到他的最大距离+1，记为f[i]

所以枚举每一个入度为零的点，从他开始更新每一个能到达的的点的f[i]

最后将每个点的f[i]加起来即为答案

虽然看着好像因为没有vis之类的东西，每个点会被访问很多遍，但是其实每个点最多只会被两个点向指，所以复杂度大约是O(n)的

大概有点dp的思想？

代码如下：

#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int d[],n,a[],f[];
long long ans=;
vector<int> g[];

void dfs(int now,int deep)
{
    f[now]=max(f[now],deep);
    for(int i=;i<g[now].size();i++)
    {
        dfs(g[now][i],deep+);
    }
}

int main()
{
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    for(int i=;i<=n;i++)
    {
        if(a[i-]>a[i])
        {
            g[i].push_back(i-);
            d[i-]++;
        }
        if(a[i]>a[i-])
        {
            g[i-].push_back(i);
            d[i]++;
        }
    }
    for(int i=;i<=n;i++)
    {
        if(!d[i])
        {
            dfs(i,);
        }
    }
    for(int i=;i<=n;i++)
    {
        ans+=f[i];
    }
    printf("%d\n",ans);
}