cf(#div1 B. Dreamoon and Sets)(数论)

B. Dreamoon and Sets

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dreamoon likes to play with sets, integers and 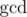. 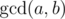is defined as the largest positive integer that divides both a and b.

Let S be a set of exactly four distinct integers greater than 0. Define S to be of rank k if and only if for all pairs of distinct elements s_i, s_j from S, .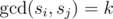

Given k and n, Dreamoon wants to make up n sets of rank k using integers from 1 to m such that no integer is used in two different sets (of course you can leave some integers without use). Calculate the minimum m that makes it possible and print one possible solution.

Input

The single line of the input contains two space separated integers n, k (1 ≤ n ≤ 10 000, 1 ≤ k ≤ 100).

Output

On the first line print a single integer — the minimal possible m.

On each of the next n lines print four space separated integers representing the i-th set.

Neither the order of the sets nor the order of integers within a set is important. If there are multiple possible solutions with minimal m, print any one of them.

Sample test(s)

Input

1 1

Output

5
1 2 3 5

Input

2 2

Output

22
2 4 6 22
14 18 10 16

Note

For the first example it's easy to see that set {1, 2, 3, 4} isn't a valid set of rank 1 since .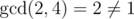

题意： 给你任意n,k,要你求出n组gcd(si,sj)=k的四个元素的组合.........

其实对于gcd(a,b)=k,我们只需要求出gcd(a,b)=1;然后进行gcd(a,b)*k=k;

不难发现这些数是固定不变的而且还有规律可循，即1,2,3,5    7 8 9 11   13 14 15 17   每一个段直接隔着2,段内前3个连续，后一个隔着2.....

代码：

 #include<cstdio>
 #include<cstring>
 using namespace std;
 const int maxn=;
 __int64 ans[maxn][];
 void work()
 {
    __int64 k=;
   for(int i=;i<;i++)
   {
       ans[i][]=k++;
       ans[i][]=k++;
       ans[i][]=k++;
       ans[i][]=++k;
       k+=;
   }
 }
 int main()
 {
   int n,k;
   work();
   while(scanf("%d%d",&n,&k)!=EOF)
   {
       printf("%I64d\n",ans[n-][]*k);
       for(int i=;i<n;i++)
         printf("%I64d %I64d %I64d %I64d\n",ans[i][]*k,ans[i][]*k,ans[i][]*k,ans[i][]*k);
   }
  return ;
 }