ID3算法决策树的生成（2）

决策树的生成，采用ID3算法（也包含了C4.5算法），使用python实现，更新了tree的保存和图示。

介绍摘自李航《统计学习方法》。

5.2.3　信息增益比

信息增益值的大小是相对于训练数据集而言的，并没有绝对意义。在分类问题困难时，也就是说在训练数据集的经验熵大的时候，信息增益值会偏大。反之，信息增益值会偏小。使用信息增益比（information gain ratio）可以对这一问题进行校正。这是特征选择的另一准则。

定义5.3（信息增益比）　特征A对训练数据集D的信息增益比g_R(D,A)定义为其信息增益g(D,A)与训练数据集D的经验熵H(D)之比：

5.3.2　C4.5的生成算法

C4.5算法与ID3算法相似，C4.5算法对ID3算法进行了改进。C4.5在生成的过程中，用信息增益比来选择特征。

算法5.3（C4.5的生成算法）

输入：训练数据集D，特征集A，阈值ε；

输出：决策树T。

（1）如果D中所有实例属于同一类C_k，则置T为单结点树，并将C_k作为该结点的类，返回T；

（2）如果A＝Ø，则置T为单结点树，并将D中实例数最大的类C_k作为该结点的类，返回T；

（3）否则，按式（5.10）计算A中各特征对D的信息增益比，选择信息增益比最大的特征A_g；

（4）如果A_g的信息增益比小于阈值，则置T为单结点树，并将D中实例数最大的类C_k作为该结点的类，返回T；

（5）否则，对A_g的每一可能值a_i，依A_g＝a_i将D分割为子集若干非空D_i，将D_i中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T，返回T；

（6）对结点i，以D_i为训练集，以A-{A_g}为特征集，递归地调用步(1)～步(5)，得到子树T_i，返回T_i。

  # coding:utf-8

 import matplotlib.pyplot as plt

 import numpy as np

 import pylab

 def createDataSet(): #贷款申请样本数据表

     dataset = [["青年", "否", "否", "一般", "拒绝"],

                ["青年", "否", "否", "好", "拒绝"],

                ["青年", "是", "否", "好", "同意"],

                ["青年", "是", "是", "一般", "同意"],

                ["青年", "否", "否", "一般", "拒绝"],

                ["中年", "否", "否", "一般", "拒绝"],

                ["中年", "否", "否", "好", "拒绝"],

                ["中年", "是", "是", "好", "同意"],

                ["中年", "否", "是", "非常好", "同意"],

                ["中年", "否", "是", "非常好", "同意"],

                ["老年", "否", "是", "非常好", "同意"],

                ["老年", "否", "是", "好", "同意"],

                ["老年", "是", "否", "好", "同意"],

                ["老年", "是", "否", "非常好", "同意"],

                ["老年", "否", "否", "一般", "拒绝"],

                ]

     labels = ["年龄", "有工作", "有房子", "信贷情况"]

     return dataset, labels

 def getList(dataset,index=-1):#返回每层列表

     alist=[i[index] for i in dataset]

     aset=list(set(alist))

     acount=[alist.count(aset[j]) for j in range(len(aset))]

     return alist,aset,acount

 def getdH(account): #计算H(D)

     t=np.sum(account)

     return np.sum([-float(a)/t*np.log2(float(a)/t) for a in account])

 def getdaH(acount,ad): #计算H(D,A)

     t=np.sum(acount)

     return np.sum([[0 if j==0 else -a*float(j)/t/a*np.log2(float(j)/a) for j in b] for a,b in zip(acount,ad)])

 def gethaD(acount): #计算Ha(D)

     t=np.sum(acount)

     return np.sum([ -float(a)/t*np.log2(float(a)/t)  for a in acount])

 def getaH(dataset,index,c4_5=0): #计算g(D,A),若c4_5=1则采用信息增益比

     dlist,dset,dcount= getList(dataset,-1)

     hd=getdH(dcount)

     alist,aset,acount=getList(dataset,index)

     ad=[[[dlist[i] for i in range(len(dlist)) if dataset[i][index]==j].count(k) for k in dset] for j in aset]

     if c4_5:

         return 0 if gethaD(acount)==0 else (hd-getdaH(acount,ad))/gethaD(acount)

     else:

         return hd-getdaH(acount,ad)

 def ID3(dataset,labels,tree=[]):#ID3算法

     dlist,dset,dcount= getList(dataset,-1)

     if len(dset)<2 :

         tree.append([dset[0],0])

         return

     adlist=[[getaH(dataset,i),i] for i in range(len(dataset[0])-1)]

     t1= max(adlist,key=lambda x: x[0])

     tree.append([labels[t1[1]],2])

     alist,aset,acount=getList(dataset,t1[1])

     for a in aset:

         tree.append([a,1])

         ID3([i for i in dataset if i[t1[1]]==a],labels,tree)

     return tree

 def showT(tree):#根据Tree列表绘制图像

     import sys

     reload(sys)

     sys.setdefaultencoding('utf-8')

     pylab .mpl.rcParams['font.sans-serif'] = ['SimHei']

     fig1 = plt.figure(1, (6, 6))

     ax = fig1.add_axes([0, 0, 1, 1], frameon=False, aspect=1.)

     x,y=0.5,0.85

     for i in range(len(tree)):

         if tree[i][1]==2:

              fig1.text(x,y, tree[i][0],ha="center",size=21,bbox=dict(boxstyle="square", fc="w", ec="k"))

              ax.arrow(x,y-0.02, 0.09,-0.11, head_width=0.01, head_length=0.02, fc='k', ec='k')

              ax.arrow(x,y-0.02, -0.09,-0.11, head_width=0.01, head_length=0.02, fc='k', ec='k')

              x+=0.05

              y-=0.1

              if i>1:tree[i-2][1]-=1

         elif tree[i][1]==1:

              fig1.text(x+0.05,y, tree[i][0],ha="center",size=21)

              x+=0.05

              y-=0.1

         else:

              fig1.text(x,y, tree[i][0],ha="center",size=21,bbox=dict(boxstyle="square", fc="w", ec="k"))

              x-=0.25

              y+=0.1

              j=i-2

              while tree[j][1]==0:

                  j=j-2

                  x+=0.1

                  y+=0.2

              tree[j][1]-=1

     ax.xaxis.set_visible(False)

     ax.yaxis.set_visible(False)

     plt.draw()

     plt.show()

 dataset,labels=createDataSet()

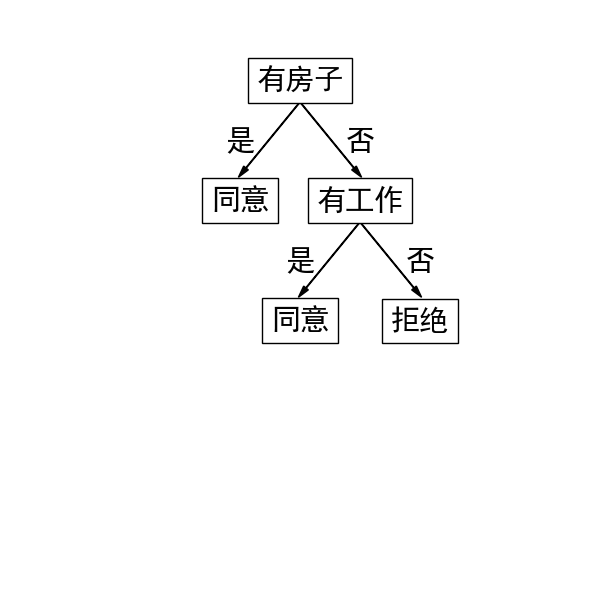
 tree= ID3(dataset,labels) #[["有房子",2],["否",1],["有工作",2],["否",1],["拒绝",0],["是",1],["同意",0],["是",1],["同意",0]]

 showT(tree)