【数据结构和算法】 O(1)时间取得栈中的最大 / 最小元素值
常数时间取得栈中的元素最大值和最小值,我们可以想到当push的时候比较一下,如果待push元素值小于栈顶元素,则更新min值,最大值亦然。
这样有个问题就是当pop的时候,就没了最大最小值。
于是上网查,方案余下:
转自 http://blog.163.com/kevinlee_2010/blog/static/169820820201092091554523/
感谢原作者! 转载此文请保留原作者链接!
/*********************转载 开始**************************/
问题描述:
对现在的Stack(栈)数据结构进行改进,加一个min()功能,使之能在常数,即O(1),时间内给出栈中的最小值。可对push()和pop()函数进行修改,但要求其时间复杂度都只能是O(1)。
解决方案:
在栈的每个元素加一个属性值 min (用于记录当前位置下面的元素的最小值),元素的值用key表示
压栈-Push:当压入的元素key小于当前栈顶元素的min值时,将新压入元素的min字段设置为新压入元素的key,否则,将新压入元素的min字段,设置为当前栈顶元素的min字段的值
(压入第一个元素时,直接设置当前 min <- key)
出栈-Pop:和以前一样删除就行
这样栈顶元素中的min字段,存储的就是栈中的最小值, 删除也不用额外的比较操作~
/*********************转载 结束**************************/
自己用代码实现之,如下
#include "stdafx.h"
#include <iostream>
#include <stack>
using namespace std;
/****************************************
*2014/04/17 14:05:08
*
*
*Describtion:
*O(1)时间取得栈中最大值和最小值
*
*****************************************/ typedef struct _tagElement
{
//用值本身来初始化min 和 max字段
struct _tagElement(int val ) : value(val), min(val), max(val){} int value; //值字段
int min; //栈中最小值
int max; //栈中最大值
}Element; size_t PushStack(stack<Element>& st, Element e)
{
if (st.size() > )
{
//如果待插入元素的value 大于 栈顶元素的min字段值,则用栈顶元素的min字段更新待插入元素的min字段
if (e.value > st.top().min)
{
e.min = st.top().min;
} //如果待插入元素的value 小于 栈顶元素的max字段值,则用栈顶元素的max字段更新待插入元素的max字段
if (e.value < st.top().max)
{
e.max = st.top().max;
}
} st.push(e); return st.size();
} int Max(stack<Element>& st)
{
if (st.size() <= )
{
return -;
}
return st.top().max;
} int Min(stack<Element>& st)
{
if (st.size() <= )
{
return -;
}
return st.top().min;
} int _tmain(int argc, _TCHAR* argv[])
{
stack<Element> st;
Element arr[] = {Element(), Element(), Element(), Element(), Element()}; for (int index = ; index < sizeof(arr) / sizeof(arr[]); ++ index)
{
size_t size = PushStack(st, arr[index]);
} cout<<"The min value of st is "<<Min(st)<<endl;
cout<<"The MAX value of st is "<<Max(st)<<endl; return ;
}
执行结果如下
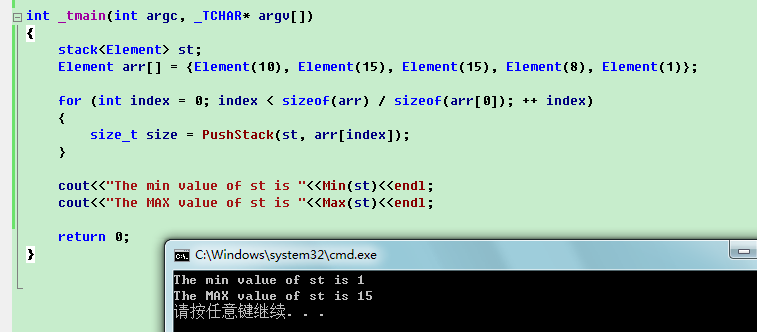
【数据结构和算法】 O(1)时间取得栈中的最大 / 最小元素值的更多相关文章
- 《剑指Offer》第20题(Java实现):定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
一.题目描述 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1)). 二.思路解析 首先定义一个Integer类型的栈,记为stack,此栈用来完成数据 ...
- 剑指offer20:定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
1 题目描述 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1)). 2. 思路和方法 利用辅助栈来存储现有栈的最小值.在入栈和出栈的时候将现有栈和最小 ...
- 《数据结构与算法之美》 <06>栈:如何实现浏览器的前进和后退功能?
浏览器的前进.后退功能,我想你肯定很熟悉吧? 当你依次访问完一串页面 a-b-c 之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面 b 和 a.当你后退到页面 a,点击前进按钮,就可以重新查看页 ...
- Java数据结构和算法(四):栈
一.简介 栈(英语:stack)又称为堆栈或堆叠,栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表.它按照先进后出的原则存储数据,先进入的数据被压入栈底(Bottom),最后的数据在 ...
- 《Java数据结构与算法》笔记-CH4-3用栈实现分隔符匹配
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; /** * 利 ...
- C语言 选择排序算法原理和实现 从数组中 找出最小的元素然后交换位置
#include <stdio.h> int main(void) { /* 选择排序算法 原理:从数组中 找出最小的元素然后交换位置: */ int a[10] = {9,5,10,7, ...
- 《Java数据结构与算法》笔记-CH4-2用栈实现字符串反转
import java.io.BufferedReader; import java.io.InputStreamReader; //用栈来实现一个字符串逆序算法 /** * 数据结构:栈 */ cl ...
- ACM山东工商 数据结构与算法 第3章 双向栈的操作
#include <stdio.h>#include <stdlib.h> #define SIZE 20//1左 偶 typedef struct hold{ int s ...
- 【python cookbook】【数据结构与算法】12.找出序列中出现次数最多的元素
问题:找出一个元素序列中出现次数最多的元素是什么 解决方案:collections模块中的Counter类正是为此类问题所设计的.它的一个非常方便的most_common()方法直接告诉你答案. # ...
随机推荐
- 将集成spring的项目从tomcat上移植到weblogic下存在的问题
当在weblogic下部署时, 1.需要jersey-servlet-xx.jar,jersey-core-xx.jar,jersey-server-xx.jar: 2.在web.xml中全局参数co ...
- dbgrid显示access备注信息
procedure TfrmAllFind.DBGrid6DrawColumnCell(Sender: TObject; const Rect: TRect; DataCol: Integer; C ...
- HorseCome
紫气东来,祝福也随之而来,喜鹊登梅,福禄也登上眉梢,马年将至,喜庆将萦绕身旁,在这个美好的日子送上我最真挚的祝福,祝身体安康. 春晓,春晓,处处绿杨芳草.山山水水,欢欢笑笑,共祝六合同春,步步登高!
- Hibernate逍遥游记-第13章 映射实体关联关系-005双向多对多(使用组件类集合\<composite-element>\)
1. <?xml version="1.0"?> <!DOCTYPE hibernate-mapping PUBLIC "-//Hibernate/Hi ...
- windows本地无法启动sqlserver服务
解决方法:进入服务列表后,选择sqlserver服务,右键然后选择属性,然后在登陆选项卡中,选择本地系统帐户,这样就可以启动sqlserver服务了
- Checked&Unchecked Exception
Java 中定义了两类异常: 1) Checked exception: 这类异常都是Exception的子类 .异常的向上抛出机制进行处理,如果子类可能产生A异常,那么在父类中也必须throws A ...
- C语言全局未初始化数据段分析
前言: 在分析C语言全局未初始化变量时,发现在目标文件中全局未初始化变量并不是直接放在bss段中. 再后来发现在两个.c文件中定义同名的全局变量,链接时居然没有发生符号重定义错误.才知道C语言弱定义的 ...
- AFNetworking使用
1.访问网络获取Json //Get方法 NSString *str = @"http://api.xxx.cc/product/found.jhtml"; NSDictionar ...
- android从应用到驱动之—camera(2)---cameraHAL的实现
本来想用这一篇博客把cameraHAL的实现和流程都给写完的.搞了半天,东西实在是太多了.这篇先写cameraHAL的基本实现框架,下一篇在具体写camerahal的流程吧. cameraHAL的实现 ...
- eclipse导入javax.servlet.*的方法
1.下载web应用服务器tomact,网址http://tomcat.apache.org/download-80.cgi 这个根据自己系统进行选择. 2.将其加压到电脑中 3.在eclipse中添加 ...
