CQOI2015 解题报告
CQOI2015终于全做完了~~~，讲一下题吧
首先这套题比起其他省选还是比较水的，就是5道题比较蛋疼
T1：[CQOI2015]选数
这道题还是比较神的。
首先给个比较神的题解：popoqqq大神的blog这个莫比乌斯反演真的不会
我们记f[i]为gcd=i*k时的个数，可以得到若数都不相等的话，i一定小于1e5（辗转相减法可得），那么当数都不相等时，答案显然为(r/(k*i)-l/(k*i)+1)^n-(r/(k*i)-l/(k*i)+1)-sigma(f[i*j])然后就能愉快的推出来啦，还有就是当l=1时要特判一下
CODE：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define mod 1000000007
typedef long long ll;
int power(ll x,ll y) {
ll ans=;
for (;y;y>>=){
if (y&) (ans*=x)%=mod;
(x*=x)%=mod;
}
return ans;
}
ll n,l,k,h;
#define maxk 100000
ll f[maxk+];
int main(){
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
ll L,H;
scanf("%lld%lld%lld%lld",&n,&k,&L,&H);
ll l=L/k,h=H/k;
if (L%k) l++;
int tmp=;
for (int i=maxk;i;i--) {
ll L=l/i,H=h/i;
if (l%i) L++;
f[i]=(power(H-L+,n)-(H-L+)+mod)%mod;
for (int j=i+i;j<=maxk;j+=i) f[i]=(f[i]-f[j]+mod)%mod;
}
if (l==) f[]++;
printf("%lld\n",f[]);
return ;
}
这不就是先求出最短路图后拆点跑个最大流么= =。直接做就行了不要考虑时间问题。。。
CODE：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
#define maxm 150000
#define maxn 1100
struct edges{
int to,next,dist;ll cap;
}edge[maxm*];
int l,next[maxn];
inline void _addedge(int x,int y,int z){
l++;
edge[l*]=(edges) {x,next[y],z,};next[y]=l*;
edge[l*+]=(edges) {y,next[x],z,};next[x]=l*+;
}
inline void addedge(int x,int y,ll z){
l++;
edge[l*]=(edges){y,next[x],,z};next[x]=l*;
edge[l*+]=(edges){x,next[y],,};next[y]=l*+;
}
ll dist[maxn];
bool b[maxn];
typedef pair<ll,int> ii;
priority_queue<ii,vector<ii>,greater<ii> > q;
#define fi first
#define se second
#define inf 0x7fffffff
#define Inf inf*1ll*inf
int n;
inline void dij(){
for (int i=;i<=n;i++) dist[i]=Inf;
dist[]=;
q.push(ii(,));
while (!q.empty()){
ii u=q.top();q.pop();
if (b[u.se]) continue;
b[u.se]=;
for (int i=next[u.se];i;i=edge[i].next)
if (dist[u.se]+edge[i].dist<dist[edge[i].to]) {
dist[edge[i].to]=dist[u.se]+edge[i].dist;
q.push(ii(dist[edge[i].to],edge[i].to));
}
}
}
int p[maxn],gap[maxn],h[maxn],s,t,N;
ll sap(int u,ll flow){
if (u==t) return flow;
ll cnt=;
for (int i=p[u];i;i=edge[i].next)
if (edge[i].cap&&h[edge[i].to]+==h[u]) {
ll cur=sap(edge[i].to,min(edge[i].cap,flow-cnt));
edge[i].cap-=cur;edge[i^].cap+=cur;
p[u]=i;
if ((cnt+=cur)==flow) return flow;
}
if (!(--gap[h[u]])) h[s]=N;
gap[++h[u]]++;
p[u]=next[u];
return cnt;
}
inline ll maxflow(){
for (int i=;i<=N;i++) p[i]=next[i];
ll flow=;
gap[]=N;
while (h[s]<N) flow+=sap(s,Inf);
return flow;
}
int main(){
freopen("network.in","r",stdin);
freopen("network.out","w",stdout);
int m;
scanf("%d%d",&n,&m);
N=n*;
for (int i=;i<=m;i++) {
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
_addedge(x,y,z);
}
dij();
memset(next,,sizeof(next));
l=;
for (int i=;i<=m*+;i+=) {
if (dist[edge[i].to]==dist[edge[i^].to]+edge[i].dist)
addedge(n+edge[i^].to,edge[i].to,Inf);
else if (dist[edge[i^].to]==dist[edge[i].to]+edge[i^].dist)
addedge(n+edge[i].to,edge[i^].to,Inf);
}
for (int i=;i<=n;i++) {
int x;
scanf("%d",&x);
addedge(i,n+i,x);
}
s=+n,t=n;
printf("%lld\n",maxflow());
return ;
}
T3：[CQOI2015]任务查询系统
描述：戳我~~~
这道题首先很明显是道裸的数据结构题啦。首先他要求在线，那么按顺序建个函数式线段树就行啦
自己太弱调了好久= =
CODE：
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
#define pb push_back
#define maxn 100100
struct qnode{
int x,y,z;
}q[maxn*];
int l;
inline void add(int x,int y,int z) {q[++l]=(qnode){x,y,z};}
bool cmp(qnode x,qnode y) {return x.x<y.x;}
struct node{int lc,rc,sum;ll s;}t[maxn*];
#define mid (l+r>>1)
int cnt=;
int ins(int x,int l,int r,int y,int z){
int root=++cnt;
t[root]=t[x];
t[root].s+=y*z;
t[root].sum+=z;
if (l==r) return root;
if (y<=mid) t[root].lc=ins(t[x].lc,l,mid,y,z);
else t[root].rc=ins(t[x].rc,mid+,r,y,z);
return root;
}
ll que(int x,int l,int r,int &k){
if (t[x].sum<=k) {
k-=t[x].sum;return t[x].s;
}
if (l==r) {ll ans=l*1ll*k;k=;return ans;}
ll ans=que(t[x].lc,l,mid,k);
if (k) ans+=que(t[x].rc,mid+,r,k);
return ans;
}
vector<int> a;
int s[maxn],e[maxn],p[maxn],root[maxn];
int main(){
int n,m;
scanf("%d%d",&n,&m);
a.pb();
for (int i=;i<=n;i++) {
scanf("%d%d%d",s+i,e+i,p+i);
e[i]++;
a.pb(s[i]);a.pb(e[i]);
}
sort(a.begin(),a.end());
a.resize(unique(a.begin(),a.end())-a.begin());
for (int i=;i<=n;i++) {
add(lower_bound(a.begin(),a.end(),s[i])-a.begin(),p[i],);
add(lower_bound(a.begin(),a.end(),e[i])-a.begin(),p[i],-);
}
sort(q+,q++l,cmp);
#define inf 10000000
for (int i=;i<=l;i++) root[q[i].x]=ins(root[q[i-].x],,inf,q[i].y,q[i].z);
ll pre=;
for (int i=;i<=m;i++) {
int x,ai,bi,ci;
scanf("%d%d%d%d\n",&x,&ai,&bi,&ci);
int k=1ll+(ai*1ll*(pre%ci)%ci+bi)%ci;
pre=que(root[upper_bound(a.begin(),a.end(),x)-a.begin()-],,inf,k);
printf("%lld\n",pre);
}
return ;
}
T4：[CQOI2015]多项式
描述：戳我~~~
又是高精度= =
首先我们可以换一下元，吧x-t换成x那就能得到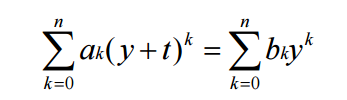
那么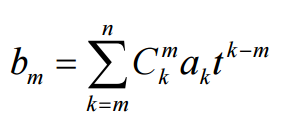
就能算5次即可啦，再考虑怎么快速算组合数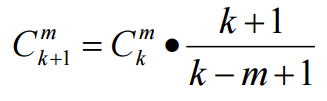
完成啦
CODE：
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxb 4
using namespace std;
char s[];
int p[]={,,,,,,,,};
struct bignum{
int a[],n,flag;
bignum(int x){
n=;memset(a,,sizeof(a));
flag=x<?:;x=abs(x);
while (x) {a[++n]=x%p[maxb];x/=p[maxb];}
if (!n) n=;
}
bignum(){n=;memset(a,,sizeof(a));flag=;}
int read(){
scanf("%s",s);
int len=strlen(s);
n=;
if (len==&&s[]=='') {a[n=]=;return ;}
for (int i=len;i>=;i-=maxb) {
int t=;
if (i>maxb) for (int j=i-maxb+;j<=i;j++) t=t*+s[j-]-'';
else for (int j=;j<=i;j++) t=t*+s[j-]-'';
a[++n]=t;
}
return ;
}
int write(){
if (flag) printf("-");
printf("%d",a[n]);
for (int i=n-;i>=;i--) {
for (int j=;j<maxb;j++) if (a[i]<p[j]) printf("");
printf("%d",a[i]);
}
printf("\n");
return ;
}
int cmp(bignum x){
if (x.n!=n) return (x.n<n);
for (int i=n;i>=;i--)
if (x.a[i]!=a[i]) return (x.a[i]<a[i]);
return -;
}
int div(int x){
int s=;
for (int i=n;i>=;i--){
s=a[i]+s*p[maxb];
a[i]=s/x;
s%=x;
}
if (n!=&&!a[n]) n--;
return s;
}
}a,b;
bignum operator + (bignum x,bignum y){
if (x.flag^y.flag && x.cmp(y)==)swap(x,y);
if (x.flag==y.flag) {
x.n=max(x.n,y.n);
for (int i=;i<=x.n;i++) {
x.a[i]+=y.a[i];
x.a[i+]+=x.a[i]/p[maxb];
x.a[i]%=p[maxb];
}
if (x.a[x.n+]) x.n++;
return x;
}
for (int i=;i<=x.n;i++) {
x.a[i]-=y.a[i];
if (x.a[i]<) {x.a[i]+=p[maxb];x.a[i+]--;}
while (!x.a[x.n]&&x.n>) x.n--;
}
return x;
}
bignum operator * (bignum x,bignum y){
bignum ans;
if (x.n==&&x.a[]==) return ans;
if (y.n==&&y.a[]==) return ans;
ans.flag=x.flag^y.flag;
for (int i=;i<=x.n;i++)
for (int j=;j<=y.n;j++) {
ans.a[i+j-]+=x.a[i]*y.a[j];
ans.a[i+j]+=ans.a[i+j-]/p[maxb];
ans.a[i+j-]%=p[maxb];
}
int n=x.n+y.n-;
while (ans.a[n+]) {
n++;ans.a[n+]+=ans.a[n]/p[maxb];
ans.a[n]%=p[maxb];
}
ans.n=n;
return ans;
}
int sum;
int main(){
static bignum n,m;
int t;
n.read();
scanf("%d",&t);
m.read();
static int a[];
a[]=;
for (int i=;i<=;i++) a[i]=(a[i-]*+) % ;
static bignum tmp=m;
int l=tmp.div();
static bignum ans,c=bignum(),T=bignum();
int cnt=;
for (bignum i=m;i.cmp(n)!=;i=i+bignum(),cnt++) {
ans=ans+c*T*bignum(a[l]);
l=(l+)%;
c=c*(i+bignum());
c.div(cnt+);
T=T*bignum(t);
}
ans.write();
return ;
}
T5:[CQOI2015]标示设计
描述：戳我~~~
首先我们考虑轮廓线，那么每个L可能有四种状态：已经结束，还未开始，还没拐弯，已经拐弯，那么如果从上到下，从左到右做的话，可以发现最多只有3条横边被标记，那么对每个L我们可以用一维来存这个状态，在加上起始状态还有终止状态就行啦，然后已经拐弯的状态一定是在那条竖边上在讨论下就行啦
由于我是从左到右，从上到下做的，所以每一维就多了1倍的状态，所以在BZ上就光荣的TLE啦，不过在学校的oj上还是能过的。所以代码就不贴啦
CQOI2015 解题报告的更多相关文章
- 重庆市队选拔 CQOI2015 解题报告
文章链接:http://www.cnblogs.com/Asm-Definer/p/4434601.html 题目链接:http://pan.baidu.com/s/1mgxIKli 官方数据:htt ...
- CH Round #56 - 国庆节欢乐赛解题报告
最近CH上的比赛很多,在此会全部写出解题报告,与大家交流一下解题方法与技巧. T1 魔幻森林 描述 Cortana来到了一片魔幻森林,这片森林可以被视作一个N*M的矩阵,矩阵中的每个位置上都长着一棵树 ...
- 二模13day1解题报告
二模13day1解题报告 T1.发射站(station) N个发射站,每个发射站有高度hi,发射信号强度vi,每个发射站的信号只会被左和右第一个比他高的收到.现在求收到信号最强的发射站. 我用了时间复 ...
- BZOJ 1051 最受欢迎的牛 解题报告
题目直接摆在这里! 1051: [HAOI2006]受欢迎的牛 Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 4438 Solved: 2353[S ...
- 习题：codevs 2822 爱在心中 解题报告
这次的解题报告是有关tarjan算法的一道思维量比较大的题目(真的是原创文章,希望管理员不要再把文章移出首页). 这道题蒟蒻以前做过,但是今天由于要复习tarjan算法,于是就看到codevs分类强联 ...
- 习题：codevs 1035 火车停留解题报告
本蒟蒻又来写解题报告了.这次的题目是codevs 1035 火车停留. 题目大意就是给m个火车的到达时间.停留时间和车载货物的价值,车站有n个车道,而火车停留一次车站就会从车载货物价值中获得1%的利润 ...
- 习题： codevs 2492 上帝造题的七分钟2 解题报告
这道题是受到大犇MagHSK的启发我才得以想出来的,蒟蒻觉得自己的代码跟MagHSK大犇的代码完全比不上,所以这里蒟蒻就套用了MagHSK大犇的代码(大家可以关注下我的博客,友情链接就是大犇MagHS ...
- 习题：codevs 1519 过路费 解题报告
今天拿了这道题目练练手,感觉自己代码能力又增强了不少: 我的思路跟别人可能不一样. 首先我们很容易就能看出,我们需要的边就是最小生成树算法kruskal算法求出来的边,其余的边都可以删掉,于是就有了这 ...
- NOIP2016提高组解题报告
NOIP2016提高组解题报告 更正:NOIP day1 T2天天爱跑步 解题思路见代码. NOIP2016代码整合
随机推荐
- 最新的thinkphp 后台入口的问题
新的thinkphp后台入口绑定了单独了文件 admin.php 要注意.
- UVa 11495 - Bubbles and Buckets
题目大意:给一个有n个数的序列,通过交换相邻的逆序数使这个序列最终有序,求需要交换的次数. 本来可以用冒泡排序解决,但是n达到105,用冒泡排序会超时,用O(nlogn)的归并排序可以达到要求.< ...
- android dialog圆角显示及解决出现的黑色棱角.(友情提示)
http://blog.csdn.net/jj120522/article/details/7871289 最近在开发一个天气预报的app,看到一个比较不错友情提示,如下: ...
- APK的反编译
有秘密的地方就有见不得光的东西,我讨厌这些,所以对于某一个XX圈APP极其反感,感觉就像一个色情网站 一.ApkTool的使用 看了几个教程,自己下载的好像总是不完整,下载包解压后一个没有aapt.e ...
- oralce
1.对数据库SQL2005.ORACLE熟悉吗? SQL2005是微软公司的数据库产品.是一个RDBMS数据库,一般应用在一些中型数据库的应用,不能跨平台. ORACLE是ORACLE公司的数 ...
- Backbone源码解读（一）事件模块
Backbone源码浅读: 前言: Backbone是早起的js前端MV*框架之一,是一个依赖于underscore和jquery的轻量级框架,虽然underscore中基于字符串拼接的模板引擎相比如 ...
- Bootstrap入门（二十三）JS插件1：模态框
Bootstrap入门(二十三)JS插件1:模态框 1.静态实例 2.动态实例 3.模态框的尺寸和效果 4.包含表单的模态框 模态框经过了优化,更加灵活,以弹出对话框的形式出现,具有最小和最实用的功能 ...
- KVO,看我就够了!
概述 KVO全称Key-Value-Observing,也叫键值监听,是一种观察者设计模式.提供了一种机制,当指定的对象的属性被修改后,对象就会收到一个通知.也就是说每次指定的被观察的对象的属性被修改 ...
- requireJS的初步掌握
前一段时间,因为一些事吧这个习惯落下了,现在争取重新捡起来. 最近开始自学requireJS,为了更好的掌握,所以写出一个自我理解的博客供参考. 分割线------------------------ ...
- linux 标准目录
转自 http://www.weixuehao.com/archives/492 装完Linux,首先需要弄清Linux 标准目录结构 / root -?启动Linux时使用的一些核心文件.如操作系统 ...