Bezier（贝塞尔）曲线简介

　　在计算机图形学中，Bezier曲线被广泛用于对平滑的曲线进行建模，对其有适当的了解是必要的。一条Bezier曲线由一系列控制点定义，称为曲线的阶数，由此可知，使用两个控制点（）可以定义一条一阶Bezier曲线，三个控制点则是二阶，以此类推。

　　Bezier曲线可以用递归的方式来定义，它是在控制点间反复地进行线性插值得到的参数曲线。一个简单的定义如下：

　　　　给定控制点，其定义了阶Bezier曲线

　　　　其中

有了这个定义，立即可以给出一个计算Bezier曲线上任意一点坐标的算法（一般来说，t在0到1之间），即原封不动地把定义翻译成编程语言。显然，这一过程中有大量的重复计算，造成了不必要的开销。打个表就能解决这个问题，当然也可以自底向上地计算，参见动态规划的思想（这玩意儿有个名字叫De Casteljau's algorithm）。

数学上，可以将递归定义的Bezier曲线参数方程展开并求出其封闭形式。它是多项式形式的：

由此，可以线性迭代地计算，且只需要常数的空间。

　　图形学中较高阶的Bezier曲线不是很常用，对于常见的二、三、四阶Bezier曲线，手动展开成多项式计算即可。

　　最后放两张Wikipedia Bezier Curve的图：

三阶Bezier曲线示例

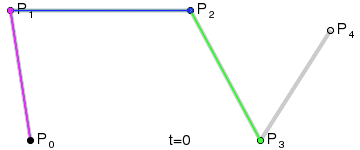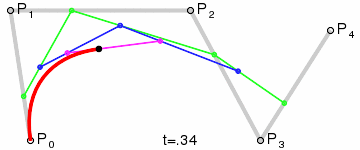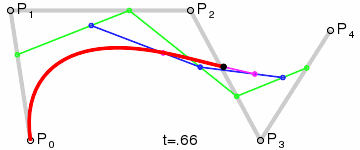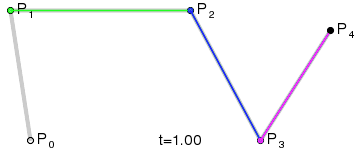
四阶Bezier曲线生成示例