Inversions After Shuffle

Inversions After Shuffle

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a permutation of integers from 1 to n. Exactly once you apply the following operation to this permutation: pick a random segment and shuffle its elements. Formally:

1. Pick a random segment (continuous subsequence) from l to r. All 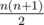 segments are equiprobable.
2. Let k = r - l + 1, i.e. the length of the chosen segment. Pick a random permutation of integers from 1 to k, p1, p2, ..., pk. All k!permutation are equiprobable.
3. This permutation is applied to elements of the chosen segment, i.e. permutation a1, a2, ..., al - 1, al, al + 1, ..., ar - 1, ar, ar + 1, ..., an is transformed to a1, a2, ..., al - 1, al - 1 + p1, al - 1 + p2, ..., al - 1 + pk - 1, al - 1 + pk, ar + 1, ..., an.

Inversion if a pair of elements (not necessary neighbouring) with the wrong relative order. In other words, the number of inversion is equal to the number of pairs (i, j) such that i < j and ai > aj. Find the expected number of inversions after we apply exactly one operation mentioned above.

Input

The first line contains a single integer n (1 ≤ n ≤ 100 000) — the length of the permutation.

The second line contains n distinct integers from 1 to n — elements of the permutation.

Output

Print one real value — the expected number of inversions. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 9.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .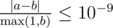

Example

input

3
2 3 1

output

1.916666666666666666666666666667
分析：仔细分析可知答案为

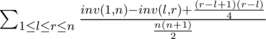　　　　，inv(l,r)代表[l,r]逆序数；

　　　 第一个和第三个值可以预处理得到；

　　　 本质是求Σ1≤l≤r≤n inv(l,r)；

　　　 从左遍历，每到一个位置，求以该位置结束的区间的逆序数；

　　　 这个可以拆为两部分，以前一个数结尾的区间的总逆序数+这个位置和前面数构成的逆序数个数；

　　　　　  求逆序对树状数组即可；注意long long；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, ls[rt]
#define Rson mid+1, R, rs[rt]
#define sys system("pause")
#define intxt freopen("in.txt","r",stdin)
const int maxn=1e5+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
inline void umax(int &p,int q){if(p<q)p=q;}
inline void umin(int &p,int q){if(p>q)p=q;}
inline ll read()
{
    ll x=;int f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int n,m,k,t;
ll a[maxn],d[maxn];
double ans,now,pre;
void add(int x,int y)
{
    for(int i=x;i<=n;i+=i&(-i))
        d[i]+=y;
}
ll get(int x)
{
    ll ret=;
    for(int i=x;i;i-=i&(-i))
        ret+=d[i];
    return ret;
}
void init()
{
    ll cnt=;
    for(int i=;i<=n;i++)
    {
        cnt+=get(n)-get(a[i]);
        add(a[i],);
    }
    for(int i=;i<=n;i++)
    ans+=(n-i+)*((double)i*(i-)/+cnt);
    memset(d,,sizeof(d));
}
int main()
{
    int i,j;
    scanf("%d",&n);
    rep(i,,n)a[i]=read();
    init();
    rep(i,,n)
    {
        now=get(n)-get(a[i])+pre;
        ans-=now;
        pre=now;
        add(a[i],i);
    }
    ans/=(double)n*(n+)/;
    printf("%.10f\n",ans);
    //system("Pause");
    return ;
}