Johnson 全源最短路径算法

解决单源最短路径问题（Single Source Shortest Paths Problem）的算法包括：

• Dijkstra 单源最短路径算法：时间复杂度为 O(E + VlogV)，要求权值非负；
• Bellman-Ford 单源最短路径算法：时间复杂度为 O(VE)，适用于带负权值情况；

对于全源最短路径问题（All-Pairs Shortest Paths Problem），可以认为是单源最短路径问题的推广，即分别以每个顶点作为源顶点并求其至其它顶点的最短距离。例如，对每个顶点应用 Bellman-Ford 算法，则可得到所有顶点间的最短路径的运行时间为 O(V²E)，由于图中顶点都是连通的，而边的数量可能会比顶点更多，这个时间没有比 Floyd-Warshall 全源最短路径算法 O(V³) 更优。那么，再试下对每个顶点应用 Dijkstra 算法，则可得到所有顶点间的最短路径的运行时间为 O(VE + V²logV)，看起来优于 Floyd-Warshall 算法的 O(V³)，所以看起来使用基于 Dijkstra 算法的改进方案好像更好，但问题是 Dijkstra 算法要求图中所有边的权值非负，不适合通用的情况。

在 1977 年，Donald B. Johnson 提出了对所有边的权值进行 "re-weight" 的算法，使得边的权值非负，进而可以使用 Dijkstra 算法进行最短路径的计算。

我们先自己思考下如何进行 "re-weight" 操作，比如，简单地对每条边的权值加上一个较大的正数，使其非负，是否可行？

   1     1     1
s-----a-----b-----c
 \              /
   \          /
     \______/
         4

比如上面的图中，共 4 条边，权值分别为 1,1,1,4。当前 s --> c 的最短路径是 {s-a, a-b, b-c} 即 1+1+1=3。而如果将所有边的权值加 1，则最短路径就会变成 {s-c} 的 5，因为 2+2+2=6，实际上导致了最短路径的变化，显然是错误的。

那么，Johnson 算法是如何对边的权值进行 "re-weight" 的呢？以下面的图 G 为例，有 4 个顶点和 5 条边。

首先，新增一个源顶点 4，并使其与所有顶点连通，新边赋权值为 0，如下图所示。

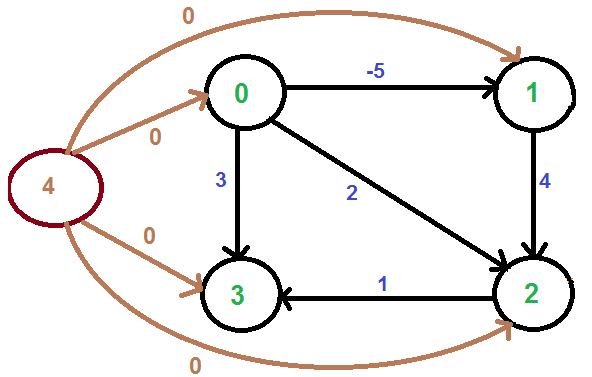
使用 Bellman-Ford 算法 计算新的顶点到所有其它顶点的最短路径，则从 4 至 {0, 1, 2, 3} 的最短路径分别是 {0, -5, -1, 0}。即有 h[] = {0, -5, -1, 0}。当得到这个 h[] 信息后，将新增的顶点 4 移除，然后使用如下公式对所有边的权值进行 "re-weight"：

w(u, v) = w(u, v) + (h[u] - h[v]).

则可得到下图中的结果：

此时，所有边的权值已经被 "re-weight" 为非负。此时，就可以利用 Dijkstra 算法对每个顶点分别进行最短路径的计算了。

Johnson 算法描述如下：

1. 给定图 G = (V, E)，增加一个新的顶点 s，使 s 指向图 G 中的所有顶点都建立连接，设新的图为 G’；
2. 对图 G’ 中顶点 s 使用 Bellman-Ford 算法计算单源最短路径，得到结果 h[] = {h[0], h[1], .. h[V-1]}；
3. 对原图 G 中的所有边进行 "re-weight"，即对于每个边 (u, v)，其新的权值为 w(u, v) + (h[u] - h[v])；
4. 移除新增的顶点 s，对每个顶点运行 Dijkstra 算法求得最短路径；

Johnson 算法的运行时间为 O(V²logV + VE)。

Johnson 算法伪码实现如下：

Johnson 算法 C# 代码实现如下：

 using System;
 using System.Collections.Generic;
 using System.Linq;

 namespace GraphAlgorithmTesting
 {
   class Program
   {
     static void Main(string[] args)
     {
       // build a directed and negative weighted graph
       Graph directedGraph1 = new Graph();
       directedGraph1.AddEdge(, , -);
       directedGraph1.AddEdge(, , );
       directedGraph1.AddEdge(, , );
       directedGraph1.AddEdge(, , );
       directedGraph1.AddEdge(, , );
       directedGraph1.AddEdge(, , );
       directedGraph1.AddEdge(, , );
       directedGraph1.AddEdge(, , -);

       Console.WriteLine();
       Console.WriteLine("Graph Vertex Count : {0}", directedGraph1.VertexCount);
       Console.WriteLine("Graph Edge Count : {0}", directedGraph1.EdgeCount);
       Console.WriteLine();

       int[,] distSet1 = directedGraph1.Johnsons();
       PrintSolution(directedGraph1, distSet1);

       // build a directed and positive weighted graph
       Graph directedGraph2 = new Graph();
       directedGraph2.AddEdge(, , );
       directedGraph2.AddEdge(, , );
       directedGraph2.AddEdge(, , );
       directedGraph2.AddEdge(, , );

       Console.WriteLine();
       Console.WriteLine("Graph Vertex Count : {0}", directedGraph2.VertexCount);
       Console.WriteLine("Graph Edge Count : {0}", directedGraph2.EdgeCount);
       Console.WriteLine();

       int[,] distSet2 = directedGraph2.Johnsons();
       PrintSolution(directedGraph2, distSet2);

       Console.ReadKey();
     }

     private static void PrintSolution(Graph g, int[,] distSet)
     {
       Console.Write("\t");
       for (int i = ; i < g.VertexCount; i++)
       {
         Console.Write(i + "\t");
       }
       Console.WriteLine();
       Console.Write("\t");
       for (int i = ; i < g.VertexCount; i++)
       {
         Console.Write("-" + "\t");
       }
       Console.WriteLine();
       for (int i = ; i < g.VertexCount; i++)
       {
         Console.Write(i + "|\t");
         for (int j = ; j < g.VertexCount; j++)
         {
           if (distSet[i, j] == int.MaxValue)
           {
             Console.Write("INF" + "\t");
           }
           else
           {
             Console.Write(distSet[i, j] + "\t");
           }
         }
         Console.WriteLine();
       }
     }

     class Edge
     {
       public Edge(int begin, int end, int weight)
       {
         this.Begin = begin;
         this.End = end;
         this.Weight = weight;
       }

       public int Begin { get; private set; }
       public int End { get; private set; }
       public int Weight { get; private set; }

       public void Reweight(int newWeight)
       {
         this.Weight = newWeight;
       }

       public override string ToString()
       {
         return string.Format(
           "Begin[{0}], End[{1}], Weight[{2}]",
           Begin, End, Weight);
       }
     }

     class Graph
     {
       private Dictionary<int, List<Edge>> _adjacentEdges
         = new Dictionary<int, List<Edge>>();

       public Graph(int vertexCount)
       {
         this.VertexCount = vertexCount;
       }

       public int VertexCount { get; private set; }

       public int EdgeCount
       {
         get
         {
           return _adjacentEdges.Values.SelectMany(e => e).Count();
         }
       }

       public void AddEdge(int begin, int end, int weight)
       {
         if (!_adjacentEdges.ContainsKey(begin))
         {
           var edges = new List<Edge>();
           _adjacentEdges.Add(begin, edges);
         }

         _adjacentEdges[begin].Add(new Edge(begin, end, weight));
       }

       public void AddEdge(Edge edge)
       {
         AddEdge(edge.Begin, edge.End, edge.Weight);
       }

       public void AddEdges(IEnumerable<Edge> edges)
       {
         foreach (var edge in edges)
         {
           AddEdge(edge);
         }
       }

       public IEnumerable<Edge> GetAllEdges()
       {
         return _adjacentEdges.Values.SelectMany(e => e);
       }

       public int[,] Johnsons()
       {
         // distSet[,] will be the output matrix that will finally have the shortest
         // distances between every pair of vertices
         int[,] distSet = new int[VertexCount, VertexCount];

         for (int i = ; i < VertexCount; i++)
         {
           for (int j = ; j < VertexCount; j++)
           {
             distSet[i, j] = int.MaxValue;
           }
         }
         for (int i = ; i < VertexCount; i++)
         {
           distSet[i, i] = ;
         }

         // step 1: add new vertex s and connect to all vertices
         Graph g = new Graph(this.VertexCount + );
         g.AddEdges(this.GetAllEdges());

         int s = this.VertexCount;
         for (int i = ; i < this.VertexCount; i++)
         {
           g.AddEdge(s, i, );
         }

         // step 2: use Bellman-Ford to evaluate shortest paths from s
         int[] h = g.BellmanFord(s);

         // step 3: re-weighting edges of the original graph
         //         w(u, v) = w(u, v) + (h[u] - h[v])
         foreach (var edge in this.GetAllEdges())
         {
           edge.Reweight(edge.Weight + (h[edge.Begin] - h[edge.End]));
         }

         // step 4: use Dijkstra for each edges
         for (int begin = ; begin < this.VertexCount; begin++)
         {
           int[] dist = this.Dijkstra(begin);
           for (int end = ; end < dist.Length; end++)
           {
             if (dist[end] != int.MaxValue)
             {
               distSet[begin, end] = dist[end] - (h[begin] - h[end]);
             }
           }
         }

         return distSet;
       }

       public int[,] FloydWarshell()
       {
         /* distSet[,] will be the output matrix that will finally have the shortest
            distances between every pair of vertices */
         int[,] distSet = new int[VertexCount, VertexCount];

         for (int i = ; i < VertexCount; i++)
         {
           for (int j = ; j < VertexCount; j++)
           {
             distSet[i, j] = int.MaxValue;
           }
         }
         for (int i = ; i < VertexCount; i++)
         {
           distSet[i, i] = ;
         }

         /* Initialize the solution matrix same as input graph matrix. Or
            we can say the initial values of shortest distances are based
            on shortest paths considering no intermediate vertex. */
         foreach (var edge in _adjacentEdges.Values.SelectMany(e => e))
         {
           distSet[edge.Begin, edge.End] = edge.Weight;
         }

         /* Add all vertices one by one to the set of intermediate vertices.
           ---> Before start of a iteration, we have shortest distances between all
           pairs of vertices such that the shortest distances consider only the
           vertices in set {0, 1, 2, .. k-1} as intermediate vertices.
           ---> After the end of a iteration, vertex no. k is added to the set of
           intermediate vertices and the set becomes {0, 1, 2, .. k} */
         for (int k = ; k < VertexCount; k++)
         {
           // Pick all vertices as source one by one
           for (int i = ; i < VertexCount; i++)
           {
             // Pick all vertices as destination for the above picked source
             for (int j = ; j < VertexCount; j++)
             {
               // If vertex k is on the shortest path from
               // i to j, then update the value of distSet[i,j]
               if (distSet[i, k] != int.MaxValue
                 && distSet[k, j] != int.MaxValue
                 && distSet[i, k] + distSet[k, j] < distSet[i, j])
               {
                 distSet[i, j] = distSet[i, k] + distSet[k, j];
               }
             }
           }
         }

         return distSet;
       }

       public int[] BellmanFord(int source)
       {
         // distSet[i] will hold the shortest distance from source to i
         int[] distSet = new int[VertexCount];

         // Step 1: Initialize distances from source to all other vertices as INFINITE
         for (int i = ; i < VertexCount; i++)
         {
           distSet[i] = int.MaxValue;
         }
         distSet[source] = ;

         // Step 2: Relax all edges |V| - 1 times. A simple shortest path from source
         // to any other vertex can have at-most |V| - 1 edges
         for (int i = ; i <= VertexCount - ; i++)
         {
           foreach (var edge in _adjacentEdges.Values.SelectMany(e => e))
           {
             int u = edge.Begin;
             int v = edge.End;
             int weight = edge.Weight;

             if (distSet[u] != int.MaxValue
               && distSet[u] + weight < distSet[v])
             {
               distSet[v] = distSet[u] + weight;
             }
           }
         }

         // Step 3: check for negative-weight cycles.  The above step guarantees
         // shortest distances if graph doesn't contain negative weight cycle.
         // If we get a shorter path, then there is a cycle.
         foreach (var edge in _adjacentEdges.Values.SelectMany(e => e))
         {
           int u = edge.Begin;
           int v = edge.End;
           int weight = edge.Weight;

           if (distSet[u] != int.MaxValue
             && distSet[u] + weight < distSet[v])
           {
             Console.WriteLine("Graph contains negative weight cycle.");
           }
         }

         return distSet;
       }

       public int[] Dijkstra(int source)
       {
         // dist[i] will hold the shortest distance from source to i
         int[] distSet = new int[VertexCount];

         // sptSet[i] will true if vertex i is included in shortest
         // path tree or shortest distance from source to i is finalized
         bool[] sptSet = new bool[VertexCount];

         // initialize all distances as INFINITE and stpSet[] as false
         for (int i = ; i < VertexCount; i++)
         {
           distSet[i] = int.MaxValue;
           sptSet[i] = false;
         }

         // distance of source vertex from itself is always 0
         distSet[source] = ;

         // find shortest path for all vertices
         for (int i = ; i < VertexCount - ; i++)
         {
           // pick the minimum distance vertex from the set of vertices not
           // yet processed. u is always equal to source in first iteration.
           int u = CalculateMinDistance(distSet, sptSet);

           // mark the picked vertex as processed
           sptSet[u] = true;

           // update dist value of the adjacent vertices of the picked vertex.
           for (int v = ; v < VertexCount; v++)
           {
             // update dist[v] only if is not in sptSet, there is an edge from
             // u to v, and total weight of path from source to  v through u is
             // smaller than current value of dist[v]
             if (!sptSet[v]
               && distSet[u] != int.MaxValue
               && _adjacentEdges.ContainsKey(u)
               && _adjacentEdges[u].Exists(e => e.End == v))
             {
               int d = _adjacentEdges[u].Single(e => e.End == v).Weight;
               if (distSet[u] + d < distSet[v])
               {
                 distSet[v] = distSet[u] + d;
               }
             }
           }
         }

         return distSet;
       }

       private int CalculateMinDistance(int[] distSet, bool[] sptSet)
       {
         int minDistance = int.MaxValue;
         int minDistanceIndex = -;

         for (int v = ; v < VertexCount; v++)
         {
           if (!sptSet[v] && distSet[v] <= minDistance)
           {
             minDistance = distSet[v];
             minDistanceIndex = v;
           }
         }

         return minDistanceIndex;
       }
     }
   }
 }

运行结果如下：

参考资料

• 广度优先搜索
• 深度优先搜索
• Breadth First Traversal for a Graph
• Depth First Traversal for a Graph
• Dijkstra 单源最短路径算法
• Bellman-Ford 单源最短路径算法
• Bellman–Ford algorithm
• Introduction To Algorithm
• Floyd-Warshall's algorithm
• Bellman-Ford algorithm for single-source shortest paths
• Dynamic Programming | Set 23 (Bellman–Ford Algorithm)
• Dynamic Programming | Set 16 (Floyd Warshall Algorithm)
• Johnson’s algorithm for All-pairs shortest paths
• Floyd-Warshall's algorithm
• 最短路径算法--Dijkstra算法，Bellmanford算法，Floyd算法，Johnson算法
• QuickGraph, Graph Data Structures And Algorithms for .NET
• CHAPTER 26: ALL-PAIRS SHORTEST PATHS

本篇文章《Johnson 全源最短路径算法》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。