FoveaBox：细节差别，另一种DenseBox+FPN的Anchor-free方案 | IEEE TIP 2020

作为与FCOS和FSAF同期的Anchor-free论文，FoveaBox在整体结构上也是基于DenseBox加FPN的策略，主要差别在于FoveaBox只使用目标中心区域进行预测且回归预测的是归一化后的偏移值，还有根据目标尺寸选择FPN的多层进行训练，大家可以学习下

 

来源：晓飞的算法工程笔记 公众号

论文: FoveaBox: Beyound Anchor-Based Object Detection

• 论文地址：https://arxiv.org/abs/1904.03797
• 论文代码：https://github.com/taokong/FoveaBox

Introduction

---

  论文认为anchor的使用不一定是最优的搜索目标的方式，且受人眼视网膜中央凹(fovea)的启发：视觉区域的中部有最高的视觉敏锐度，所以提出了anchor-free目标检测方法FoveaBox。

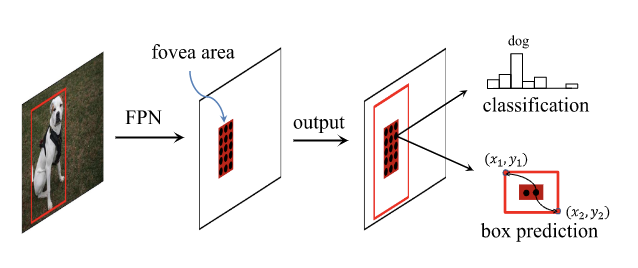
  FoveaBox联合预测每个有效位置为目标中心的可能性及其对应目标的尺寸，输出类别置信度以及用以转化目标区域的尺寸信息。如果大家看过很多Anchor-free的检测方案，可能觉得论文的实现方案很常见，的确，其实这篇文章也是Anchor-free井喷初期的作品，整体思路很纯粹，也是很多大佬都想到的思路，在阅读时需要关注以下细节：

• 以目标的中心区域进行分类预测与回归预测
• 将回归预测的是归一化后的偏移值
• 训练时可指定FPN多层同时训练
• 提出特征对齐模块，使用回归的输出来调整分类的输入特征

FoveaBox

---

Object Occurrence Possibility

  给定GT目标框\((x_1, y_1, x_2, y_2)\)，将其映射到特征金字塔层\(P_l\)：

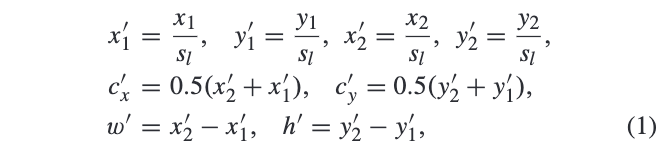
  \(s_l\)为特征层相对于输入的stride，正样本区域\(R^{pos}\)为大致为映射框的缩小版本：

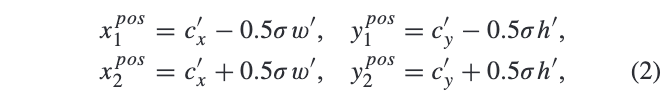
  \(\sigma\)为人为设定缩放因子。在训练阶段，正样本区域内的特征点标记为对应的目标类别，其余的区域为负样本区域，特征金字塔每层的输出为\(C\times H\times W\)，\(C\)为类别总数。

Scale Assignment

  网络的目标是预测目标的边界，直接预测是不稳定的，因为目标尺寸的跨度很大。为此，论文将目标尺寸归为多个区间，对应特征金字塔各层，各层负责特定尺寸范围的预测。给予特征金字塔\(P_3\)到\(P_7\)基础尺寸\(r_l=2^{l+2}\)，则层\(l\)负责的目标尺寸范围为：

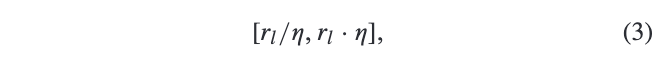
  \(\eta\)为人工设置的参数，用于控制特征金字塔每层的回归尺寸范围，不在该层尺寸范围内的训练目标则忽略。目标可能落到多个层的尺寸范围内，这时使用多层进行训练，多层训练有以下好处：

• 邻接的特征金字塔层通常有类似的语义信息，可同时进行优化。
• 大幅增加每层的训练样本数，使得训练过程更稳定。

Box Prediction

  在预测目标尺寸时，FoveaBox直接计算正样本区域\((x,y)\)到目标边界的归一化的偏移值：

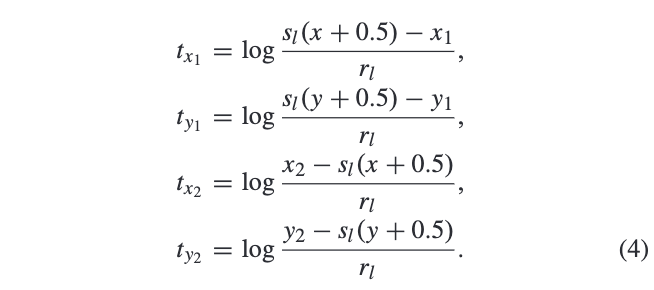
  公式4先将特征金字塔层的像素映射回输入图片，再进行偏移值的计算，训练采用L1损失函数。

Network Architecture

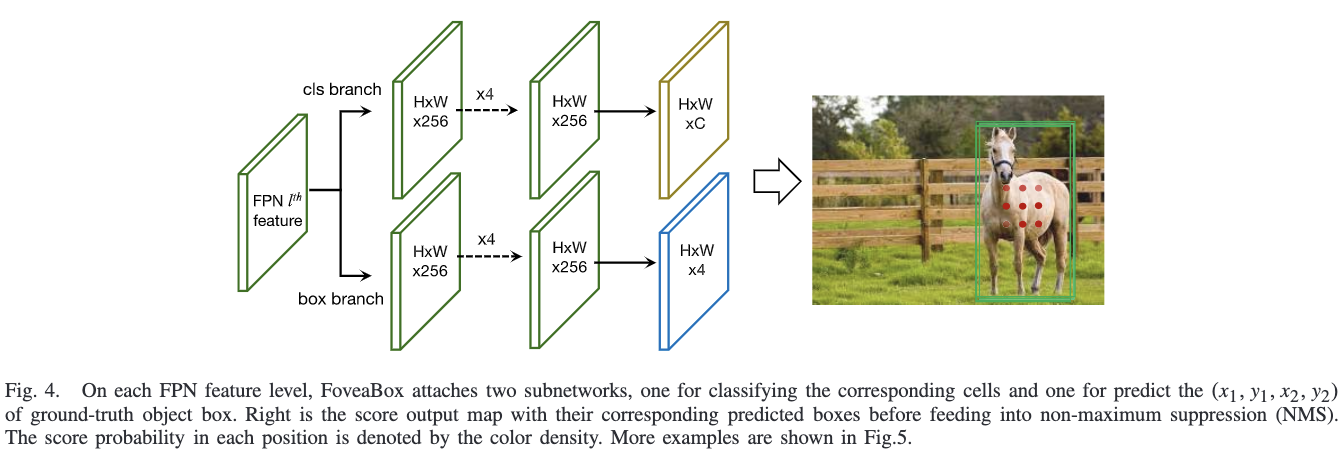
  网络结构如图4所示，主干网络采用特征金字塔的形式，每层接一个预测Head，包含分类分支和回归分支。论文采用较简单的Head结构，使用更复杂的Head可以获得更好的性能。

Feature Alignment

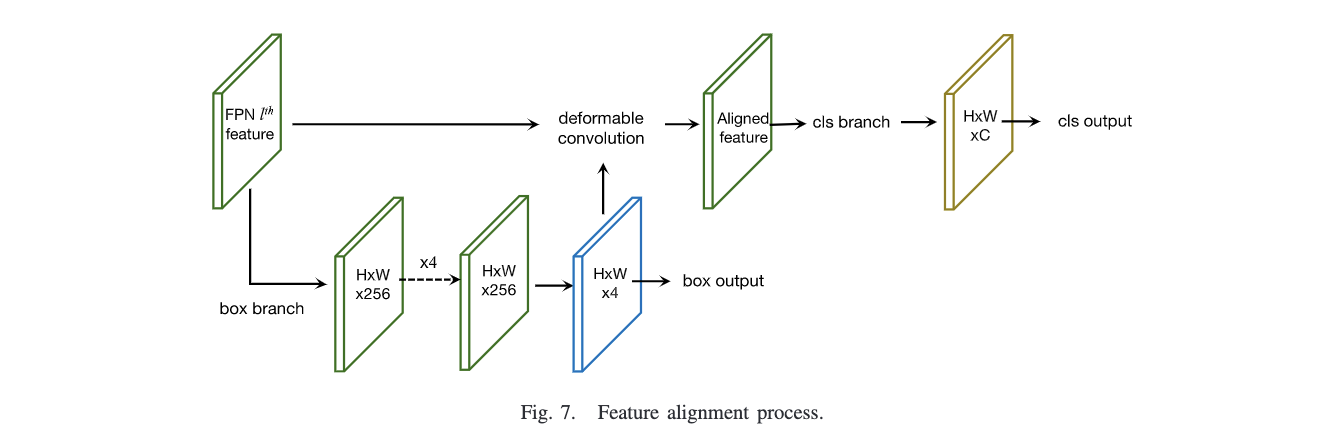
  论文提出了特征对齐的trick，主要是对预测Head进行改造，结构如图7所示，

Experiment

---

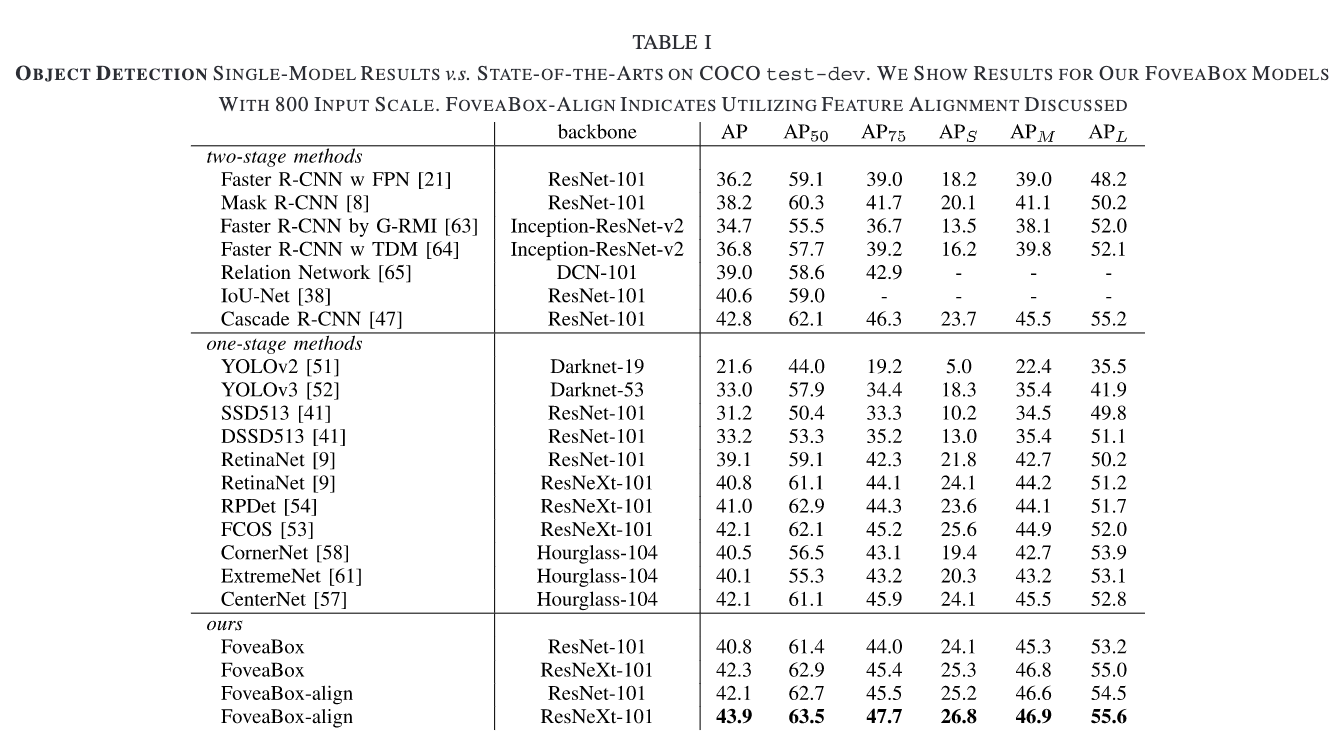
  与SOTA方法进行对比。

Conclusion

---

  作为与FCOS和FSAF同期的Anchor-free论文，FoveaBox在整体结构上也是基于DenseBox加FPN的策略，主要差别在于FoveaBox只使用目标中心区域进行预测且回归预测的是归一化后的偏移值，还有根据目标尺寸选择FPN的多层进行训练。由于FoveaBox的整体实现方案太纯粹了，与其它Anchor-free方法很像，所以一直投稿到现在才中了，作者也是相当不容易。

 

 

 

如果本文对你有帮助，麻烦点个赞或在看呗～

更多内容请关注 微信公众号【晓飞的算法工程笔记】