决策树之PEP(悲观剪枝)

引用这2篇文章

https://blog.csdn.net/taoqick/article/details/72818496

https://www.open-open.com/lib/view/open1436689999779.html

悲观错误剪枝法是根据剪枝前后的错误率来判定子树的修剪。该方法引入了统计学上连续修正的概念弥补REP中的缺陷，在评价子树的训练错误公式中添加了一个常数，假定每个叶子结点都自动对实例的某个部分进行错误的分类。

把一颗子树（具有多个叶子节点）的分类用一个叶子节点来替代的话，在训练集上的误判率肯定是上升的，但是在新数据上不一定。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。对于一颗叶子节点，它覆盖了N个样本，其中有E个错误，那么该叶子节点的错误率为（E+0.5）/N。这个0.5就是惩罚因子，那么一颗子树，它有L个叶子节点，那么该子树的误判率估计为：

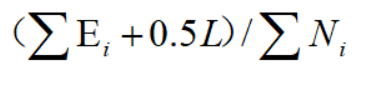
这样的话，我们可以看到一颗子树虽然具有多个子节点，但由于加上了惩罚因子，所以子树的误判率计算未必占到便宜，剪枝后内部节点变成了叶子节点，其误判个数J也需要加上一个惩罚因子，变成J+0.5。那么子树是否可以被剪枝就取决于剪枝后的错误J+0.5在的标准误差内。

我们来介绍几种定义：

n(t)为t的所有样本数

e(t)为t中不属于节点t所标识类别的样本数

在剪枝时，我们使用 r(t)=e(t)/n(t) 就是当节点被剪枝后在训练集上的错误率

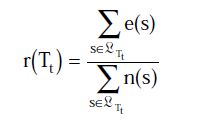而其中s为t节点的叶子节点。

我们需要矫正上面的式子

r‘(t)=[e(t) + 1/2]/n(t)  和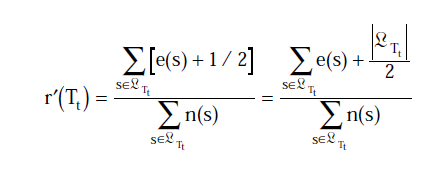  

其中s为t节点的叶子节点，你不认识的那个符号为 t的所有叶子节点的数目

为了简单，我们就只使用错误数目而不是错误率了，如下：

接着求e'(Tt)的标准差，由于误差近似看成是二项式分布，根据u = np, σ2=npq可以得到：

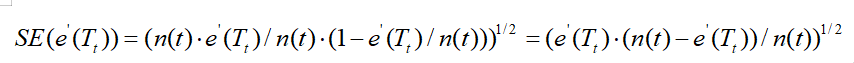
当节点t满足：

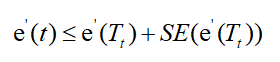
则Tt就会被裁减掉。

例如：

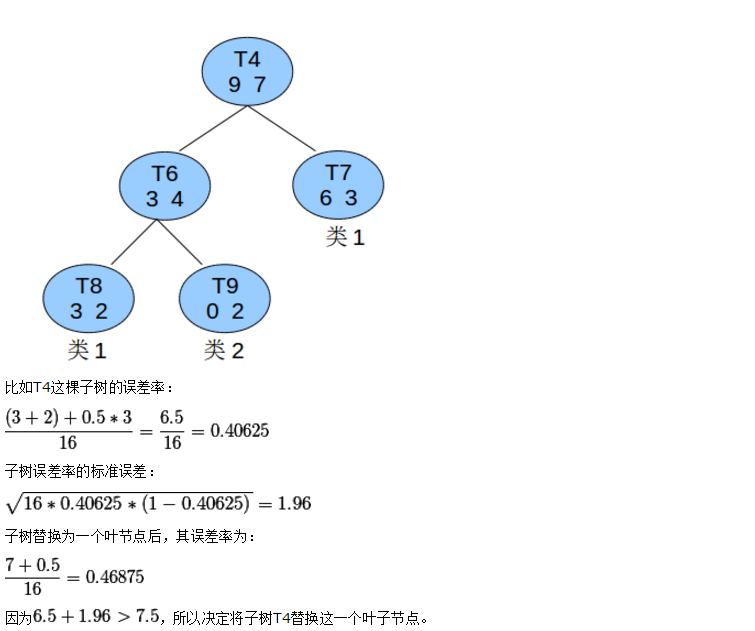
悲观剪枝的准确度比较高，但是依旧会存在以下的问题：

1.PeP算法实用的从从上而下的剪枝策略，这种剪枝会导致和预剪枝同样的问题，造成剪枝过度。

2.Pep剪枝会出现剪枝失败的情况。