矩阵LU分解
有如下方程组 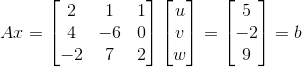 ,当矩阵 A 各列向量互不相关时, 方程组有位移解,可以使用消元法求解,具体如下:
,当矩阵 A 各列向量互不相关时, 方程组有位移解,可以使用消元法求解,具体如下:
使用消元矩阵将 A 变成上三角矩阵 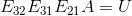 ,
,
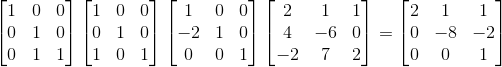 ,
,
使用消元矩阵作用于向量 b,得到向量 c,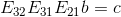 ,
,
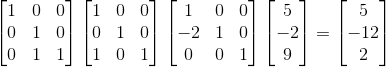 ,
,
Ax=b 消元后变为 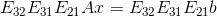 ,即
,即 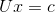 , 由于
, 由于  为上三角矩阵, 使用回带法即可求解方程组。
为上三角矩阵, 使用回带法即可求解方程组。
对矩阵 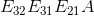 做如下运算
做如下运算 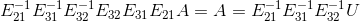 。在消元过程中,已知
。在消元过程中,已知 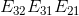 ,如何求解
,如何求解 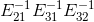 呢?
呢?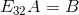 表示将矩阵A的第二行乘以 1 再加上矩阵A的第三行得到矩阵B的第三行,矩阵B的第一二行于矩阵A的第一二行保持一致。根据语义,
表示将矩阵A的第二行乘以 1 再加上矩阵A的第三行得到矩阵B的第三行,矩阵B的第一二行于矩阵A的第一二行保持一致。根据语义,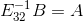 表示将矩阵B的第二行乘以 -1 再加上矩阵B的第三行得到矩阵A的第三行,矩阵A的第一二行于矩阵B的第一二行保持一致。
表示将矩阵B的第二行乘以 -1 再加上矩阵B的第三行得到矩阵A的第三行,矩阵A的第一二行于矩阵B的第一二行保持一致。
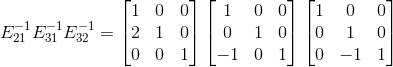 ,
,
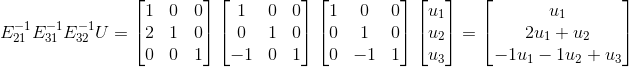 ,
,
通过以上观察,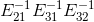 仅需将对角线下元素相加即可得到,
仅需将对角线下元素相加即可得到,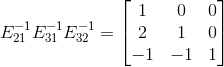 ,在矩阵消元过程中,对消元系数取反,然后放在相应的位置即构成了
,在矩阵消元过程中,对消元系数取反,然后放在相应的位置即构成了 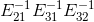 ,也就是 L 。同时,消元法记录下了 U,则有 Ux=c, b=Lc。
,也就是 L 。同时,消元法记录下了 U,则有 Ux=c, b=Lc。
由于 L 为下三角矩阵,根据 Lc=b, 可求解 c;U 为上三角矩阵, 根据 Ux=c 可求解 x。
在消元过程中,如果遇到主元位置上为 0 情况时,需要使用行变换矩阵使消元过程得以继续,PAx=Pb,P为行变换矩阵,记录矩阵 L,U,P,可实现LU分解,过程如下:
有方程组 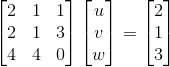 ,对矩阵
,对矩阵 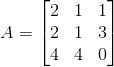 进行LU分解:
进行LU分解:
1)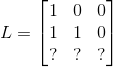 ,
, 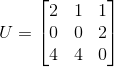 ,
,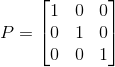 ;
;
2)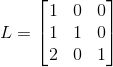 ,
,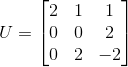 ,
,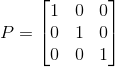 ;
;
3)由于 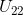 为 0,需要交换2,3行,则有:
为 0,需要交换2,3行,则有:
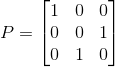 ,
, 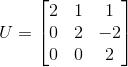 ,
,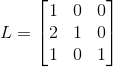 ,交换L矩阵中小于第二列下变换因子位置,即交换
,交换L矩阵中小于第二列下变换因子位置,即交换 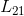 与
与  元素位置;
元素位置;
4)由于 Lc=Pb, 可计算出 c:
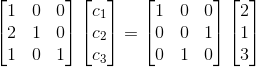 ,
, 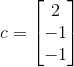 ;
;
5)由于 Ux=c,可计算出 x:
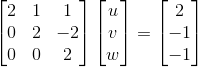 ,
,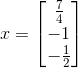 。
。
参考资料 Linear Algebra And Its Applications Gilbert Strang
矩阵LU分解的更多相关文章
- 矩阵LU分解的MATLAB与C++实现
一:矩阵LU分解 矩阵的LU分解目的是将一个非奇异矩阵\(A\)分解成\(A=LU\)的形式,其中\(L\)是一个主对角线为\(1\)的下三角矩阵:\(U\)是一个上三角矩阵. 比如\(A= \beg ...
- 矩阵LU分解分块算法实现
本文主要描述实现LU分解算法过程中遇到的问题及解决方案,并给出了全部源代码. 1. 什么是LU分解? 矩阵的LU分解源于线性方程组的高斯消元过程.对于一个含有N个变量的N个线性方程组,总可以用高斯消去 ...
- 矩阵LU分解程序实现(Matlab)
n=4;%确定需要LU分解的矩阵维数 %A=zeros(n,n); L=eye(n,n);P=eye(n,n);U=zeros(n,n);%初始化矩阵 tempU=zeros(1,n);tempP=z ...
- 计算方法 -- 解线性方程组直接法(LU分解、列主元高斯消元、追赶法)
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> ...
- MATLAB矩阵的LU分解及在解线性方程组中的应用
作者:凯鲁嘎吉 - 博客园http://www.cnblogs.com/kailugaji/ 三.实验程序 五.解答(按如下顺序提交电子版) 1.(程序) (1)LU分解源程序: function [ ...
- 线性代数笔记10——矩阵的LU分解
在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积).LU分解主要应用在数值分析 ...
- 矩阵分解---QR正交分解,LU分解
相关概念: 正交矩阵:若一个方阵其行与列皆为正交的单位向量,则该矩阵为正交矩阵,且该矩阵的转置和其逆相等.两个向量正交的意思是两个向量的内积为 0 正定矩阵:如果对于所有的非零实系数向量x ,都有 x ...
- 第五节、矩阵分解之LU分解
一.A的LU分解:A=LU 我们之前探讨过矩阵消元,当时我们通过EA=U将A消元得到了U,这一节,我们从另一个角度分析A与U的关系 假设A是非奇异矩阵且消元过程中没有行交换,我们便可以将矩阵消元的EA ...
- matlab 求解线性方程组之LU分解
线性代数中的一个核心思想就是矩阵分解,既将一个复杂的矩阵分解为更简单的矩阵的乘积.常见的有如下分解: LU分解:A=LU,A是m×n矩阵,L是m×m下三角矩阵,U是m×n阶梯形矩阵 QR分解: 秩分解 ...
随机推荐
- 鲜为人知的一些meta标签作用
来自UC Scrat-team http://scrat-team.github.io/ <meta name="viewport" content="width= ...
- HDU 1312 Red and Black (DFS & BFS)
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=1312 题目大意:有一间矩形房屋,地上铺了红.黑两种颜色的方形瓷砖.你站在其中一块黑色的瓷砖上,只能向相 ...
- TestNG中 ITestListener 的使用
1.关于testng中ITestListener 的相关介绍文档,请参考: http://javadox.com/org.testng/testng/6.8.7/org/testng/ITestLis ...
- 【爬虫】将 Scrapy 部署到 k8s
一. 概述 因为学习了 docker 和 k8s ,不管什么项目都想使用容器化部署,一个最主要的原因是,使用容器化部署是真的方便.上一篇文章 [爬虫]从零开始使用 Scrapy 介绍了如何使用 scr ...
- JUC之线程池的实现原理以及拒绝策略
线程池实现原理 向线程池提交任务后,线程池如何来处理这个任务,之前我们了解了7个参数,我们通过这些参数来串联其线程池的实现原理. 1.在创建了线程池后,开始等待请求 2.当调用execute()方法添 ...
- jQuery ajax get与post后台交互中的奥秘
这两天在做关注功能模块(类似于Instagram).多处页面都需要通过一个"关注"按钮进行关注或者取消该好友的操作.一个页面对应的放一个按钮,进行操作.效率低维护性差.因此想通过j ...
- 使用Cesium Stories在3D Tilesets中检查Features
Cesium中文网:http://cesiumcn.org/ | 国内快速访问:http://cesium.coinidea.com/ 我们创建了3D Tiles用以流式化.可视化和分析大量的三维内容 ...
- 解决vscode下载很慢的问题
1.打开vscode官网,https://code.visualstudio.com; 2.点击下载稳定版;这里我的电脑是win10版本 3.下载时可以去谷歌的下载内容里面,看到正在下载的vscode ...
- sqoop如何指定pg库的模式
摘要:sqoop如何指定pg库的模式? 本文分享自华为云社区<[Hadoop]关于Sqoop导出数据到postgresql时schema的设置问题>,作者:Copy工程师 . 说明 使用s ...
- Python的开发环境
Python的开发环境 在 Python 开发环境中我们能看到很多工具,如 pip .conda .poetry . virtualenv . venv . pyenv 等等.他们是什么,都有什么作用 ...
