OO第一单元总结-多项式求导

OO第一单元总结-多项式求导

一、第一、第二次作业总结

　　因为前两次作业设计复杂度差别不大，因而放在这里统一总结。

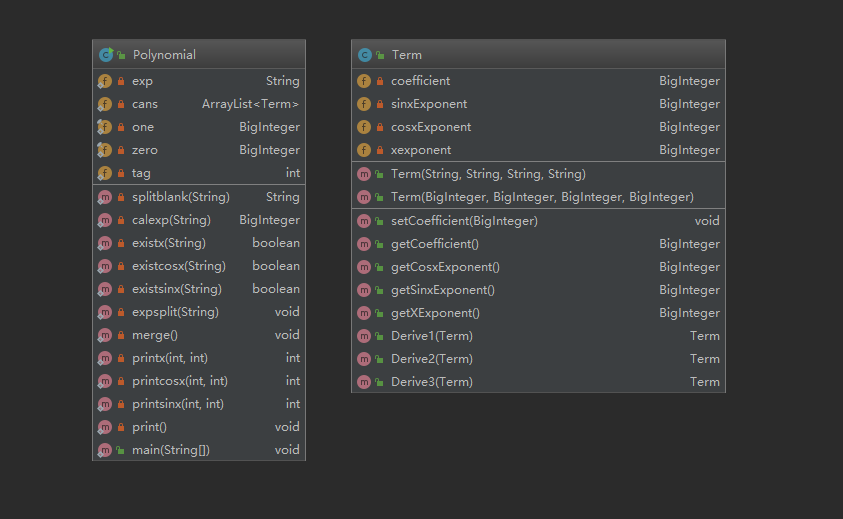
基于度量分析程序结构：

前两次作业确实存在缺乏可拓展设计的构想，基本还是面向过程的思维方式。“一类到底，一main到底”，因为有代码风格的要求被迫将代码模块化（捂脸）。

初次接触正则表达式，第一次设计正则表达式的时候并不知道正则的内部实现，出现了“一个大正则”，后来了解到许多正则匹配模式（贪婪，懒惰，独占）。两次作业都改成了小正则匹配同时捕获，这样可以有效避免正则爆栈的问题。

String expon = "[\\t ]*(\\^[\\t ]*[+-]{0,1}\\d{1,}){0,1}[\\t ]*";//指数
String subterm = "([\\t ]*(\\*[\\t ]*" +        //后续表达式
        "(((cos[\\t ]*\\([\\t ]*x[\\t ]*\\)[\\t ]*)|" +
        "(sin[\\t ]*\\([\\t ]*x[\\t ]*\\)[\\t ]*)|x)" +
        expon + "|([+-]{0,1}\\d{1,}[\\t ]*))))*";
String regax1 = "([\\t ]*\\d{1,}[\\t ]*" + subterm +
        "|([\\t ]*((cos[\\t ]*\\([\\t ]*x[\\t ]*\\)[\\t ]*)|" +
        "(sin[\\t ]*\\([\\t ]*x[\\t ]*\\)[\\t ]*)|x)" +
        "(" + expon  + subterm  + "|" + subterm + ")" + ")" +
        "|([\\t ]*[+-]\\d{1,}"  + subterm + ")" +
        ")";
String regex = "([\\t ]*[+-][\\t ]*" +      //表达式开头
                "((((cos[\\t ]*\\([\\t ]*x[\\t ]*\\)[\\t ]*)|(sin[\\t ]*\\([\\t ]*x[\\t ]*\\)[\\t ]*)|x)" + expon + subterm + ")" +
                "|([+-]" + regax1 + ")" +
                "|(\\d{1,}[\\t ]*"  + subterm + ")" +
                ")[\\t ]*)";

　　设计正则表达式时，我运用了简单的树结构，因为每个项的第一个因子较为特殊，所以单独设计，每个项的后续因子具有重复性，所以统一设计。（其实就是暴力列举所有情况）

　　求导处理方面，因为没有很好考虑到可拓展性，简单的暴力求导，公式如下：

 　　　　$(ax^bsin(x)^ccos(x)^d)′=abx^{b-1}cos(x)^dsin(x)^c+acx^bcos(x)^{d+1}sin(x)^{c−1}−adx^bcos(x)^{d−1}sin(x)^{c+1}$

　　存储方面，利用Arraylist存储每一个项，每个项内存储各个因子的指数。因为后来才解了Hashmap，发现对于前两次作业，Hashmap比ArrayList合并时有更大优势。

程序bug分析

　　bug主要存在于输出方面的，因为优化时想去除常数因子为0的项，因为考虑不周，所以出现+0无输出的bug。

发现别人bug的策略

　　1、聚焦于WF检测，根据自己设计的正则反向构造许多反例，但是发现大家WF写的都很好，确实难顶。

　　2、设计一些边缘数据，比如0*sin(x)^0。（在我那个组基本没用，大家都统一设计，未发现刁钻数据一刀hack1人以上）

　　3、借别人的数据来测·····难顶

　　4、写了个shell脚本，能用操作系统的知识解决一次测一组人的实际需求（太顶了）

二、第三次作业总结

　　这次作业简直就是地狱，周五发指导书，本来还想沿用前两次的正则构造思想，大量查阅资料，发现要递归定义正则（自己定义自己），实在是写不出来，放弃了这个选择。周六周天毫无头绪，周一了解到了一个递归下降的算法，看懂代码之后本来想拿来主义变成自己的，但是无奈自己无法复现如此精妙的递归下降，周二凌晨3点重构，从头开始。

本次作业主要分成两个工作：

　　1、WF判断，这一部分我并不想前两次，在处理之前就判断，而是考虑到括号的递归存在，所以在处理时如果不符合简单小正则规范，则输出WF（在这之前有“错误符号检测”“空格及制表符模式检测”“+-符号个数检测”）。

　　2、求导，针对这次作业十分复杂的特性，使用递归求导：

　　　　1）、Poly求导结果为Poly中的Term求导相加

　　　　2）、Term求导为Term中每个Factor求导后与剩余所有Factor相乘；

　　　　3）、Factor求导分为5大类：x、sin(x)、cos(x)、constant、Polyfactor，其中Polyfactor求导遵循1）规则

　　表达式处理是我认为本次作业最难的部分，我采用的（借鉴的）办法是，用+将Poly分成Term（在这之前用栈的方式，标记处于每个Term外的+，将Term内的+换成别的符号），然后用*将Term分成Factor（分成Factor过程分为5类，同时进行简单小正则WF判断），进而求导。（这里注意，在求导前，所有构造已经完成，即已经将所有表达式因子（Polyfactor）拆分成新的Term）

　　(Poly和Term之间不存在继承关系，Factor与其他5个因子均为继承关系)

三、说说自己的理解

　　以上即为我的方法（借鉴吸收别人的方法），下面我想重点介绍我理解的（仅仅个人理解，欢迎大牛指导批评），仅针对本题的递归下降算法：

　　递归下降算法在本题主要针对于表达式处理，因为代码版权属于别人（我真菜），就不贴代码了，简单介绍一下：

　　　　1）、各个类的构造办法比较平凡，和我的办法中类的构造大同小异。

　　　　2）、在判定表达式WF中（前提是已经进行了“无效字符检查”“空格格式检查”），采用的方式是将问题下放，在最终的各个因子中进行“小正则”的简单检查。

　　　　　　eg：sin((x)

　　　　　　整体方法：调用toPoly（）方法，toPoly（）方法中调用toTerm（）方法，toTerm（）方法中调用toFactor（）方法，toFactor（）方法先检测到这属于sin类，判断“sin(” 是否存在且合法，然后跳过，接着对于中间的部分进行toFactor（）方法继续构造（根据定义，sin括号内必须为一个5种因子（constant，sin，cos，x，Polyfactor）中的一种），接着回到toFactor（）方法，检测后面的“)”，即完成了Sin（Factor）检查，（至于Factor是否合法，那是Factor的事）。

　　　　　　追踪本eg：toFactor（）方法，判断“sin(” 存在且合法后，跳过“sin(”，接着对于中间的部分使用toFactor（）方法继续构造，在toFactor中发现了一个‘（’，因此判断它为一个Polyfactor类型的Factor，继续调用toPolyFactor（）方法，toPolyFactor（）方法构造完毕（结果为取出了“（x）”）后返回至最初的toFactor（）方法检查最后的“）”，发现没有这个“）”，因为已经将“）”匹配给了里面的“（x）”，进而抛出异常，输出WF。

　　　　3）、这种方法我读懂之后让我惊叹大自然的鬼斧神工（还有自己真菜）。个人认为它的精妙之处在于，他不关注顶层Poly如何构造，只需要知道Poly是一个一个Term构成的；同时也不需要知道Term怎么构造，因为它是一个一个Factor构成的。所有所有的问题只存在于，如何写出正确的Factor构造（这相对简单很多啊）。所有表达式提取问题迎刃而解。

　　　　看完这份代码，我感觉到自己的渺小与可怜兮兮。仅仅针对本题，我认为这个递归下降的思想也许蕴含了面向对象的很多道理，不关心大问题的具体实现，只关心大问题可以由解决哪些小问题来解决，然后利用对象或方法来解决小问题，在这点上，差不多是我第三次作业的最大收获了。

（默默感谢对我提供帮助的大牛们）