【LeetCode】1135. Connecting Cities With Minimum Cost 解题报告 (C++)

作者：负雪明烛
id： fuxuemingzhu
个人博客：http://fuxuemingzhu.cn/

题目描述

There are N cities numbered from 1 to N.

You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together. (A connection is bidirectional: connecting city1 and city2 is the same as connecting city2 and city1.)

Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return -1.

Example 1:

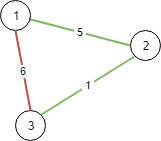
Input: N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]

Output: 6

Explanation:

Choosing any 2 edges will connect all cities so we choose the minimum 2.

Example 2:

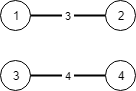
Input: N = 4, connections = [[1,2,3],[3,4,4]]

Output: -1

Explanation:

There is no way to connect all cities even if all edges are used.

Note:

1 <= N <= 10000
1 <= connections.length <= 10000
1 <= connections[i][0], connections[i][3] <= N
0 <= connections[i][2] <= 10^5
connections[i][0] != connections[i][4]

题目大意

想象一下你是个城市基建规划者，地图上有 N 座城市，它们按以 1 到 N 的次序编号。
给你一些可连接的选项 conections，其中每个选项 conections[i] = [city1, city2, cost] 表示将城市 city1 和城市 city2 连接所要的成本。（连接是双向的，也就是说城市 city1 和城市 city2 相连也同样意味着城市 city2 和城市 city1 相连）。
返回使得每对城市间都存在将它们连接在一起的连通路径（可能长度为 1 的）最小成本。该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务，则请你返回 -1。

解题方法

Kruskal算法

本题是标准的最小生成树问题，有Prim和Kruskal算法两个解法。

MST（Minimum Spanning Tree，最小生成树）问题有两种通用的解法，Prim算法就是其中之一，它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。

Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列，接着按照顺序选取每条边，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止。至于怎么合并到一个集合，那么这里我们就可以用到一个工具——-并查集。换而言之，Kruskal算法就是基于并查集的贪心算法。

具体做法如上所言，不再赘述。

C++代码如下：

class Solution {

public:

    int minimumCost(int N, vector<vector<int>>& connections) {

        part = N;

        parent = vector<int>(N, 0);

        for (int i = 0; i < N; ++i)

            parent[i] = i;

        sort(connections.begin(), connections.end(),

             [](const vector<int>& a, const vector<int>& b) { return a[2] < b[2];});

        int res = 0;

        for (vector<int>& conn : connections) {

            int a = conn[0] - 1;

            int b = conn[1] - 1;

            int cost = conn[2];

            int pa = find(a);

            int pb = find(b);

            if (pa != pb) {

                uni(a, b);

                res += cost;

            }

            if (part == 1)

                return res;

        }

        return -1;

    }

    int find(int a) {

        if (parent[a] == a)

            return a;

        return find(parent[a]);

    }

    void uni(int a, int b) {

        int pa = find(a);

        int pb = find(b);

        if (pa == pb)

            return;

        parent[pa] = pb;

        part --;

    }

private:

    vector<int> parent;

    int part = 0;

};

参考资料：
https://www.cnblogs.com/fzl194/p/8722989.html
https://www.cnblogs.com/fzl194/p/8723325.html

日期

2019 年 9 月 23 日 —— 昨夜睡的早，错过了北京的烟火