列生成算法（求解Cutting Stock问题）

列生成是用于求解大规模线性优化问题的一种算法，其实就是单纯形法的一种形式。单纯性可以通过不断迭代，通过换基变量的操作，最终找到问题的最优解。但是当问题的规模很大之后，变量的个数就会增大到在有限时间内无法有效迭代求解。所以可以用列生成方法求解，列生成方法可以一开始不列举所有的列，通过不断给模型中加入列的方式，最终找到全部解，其关键点就是加新列的过程，可以只加入能让目标值更优的列，从而减少变量的使用个数。

列生成算法流程

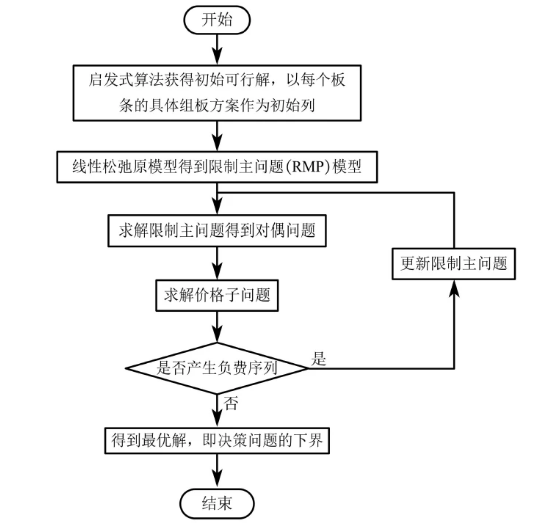
列生成过程中，需要将问题建模为主问题+子问题的形式。

主问题：就是原问题，主要用于决策是否选用某些方案（列）

主问题松弛问题：将主问题变量范围正整数松弛到正数

限制主问题：主问题去掉一部分列

限制主问题对偶问题：对限制主问题求对偶

价格子问题：原问题的局部问题，用于生成新的方案（列）

求解Cutting Stock问题

问题描述：

将一些钢管切割成为需要的长度以满足客户需求，要求使用的钢管最少。

每根钢管长度L=16m

需求：3m钢管25根；6m钢管20根，7米钢管18根

模型建立

主问题

\[min\sum_{j \in J} x_{j}\\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\sum_{j \in J} x_j a_{ij} \ge d_i \qquad \forall i \in I\\
x_j \in Z \qquad \qquad \quad \forall j \in J \]

\(x_j\): 方案选用的个数

\(a_{ij}\): 方案\(j\)中钢管\(i\)的个数

\(d_i\): 钢管\(i\)的需求量

主问题松弛问题

\[min\sum_{j \in J} x_{j}\\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\sum_{j \in J} x_j a_{ij} \ge d_i \qquad \forall i \in I\\
x_j \ge 0 \qquad \qquad \quad \forall j \in J \]

变量是整数的情况下无法用列生成法求得最优解，需要将问题松弛。如果需要求得整数最优解需要结合分支定界算法。

限制主问题

\[min\sum_{j \in J} x_{j}\\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\sum_{j \in J} x_j a_{ij} \ge d_i \qquad \forall i \in I\\
x_j \ge 0 \qquad \qquad \quad \forall j \in \Omega_j \]

将主问题中的变量规模减小，一开始只加入一部分可行的切割方案（\(a_j\)，列），列生成就是不断生成新的\(a_j\) 加入到问题中。判断一个列是否可以加入到问题，需要判断检验数\(\sigma_j = c_j - c_B B^{-1}a_j\),如果检验数为负，就可以将新的列加入。其中\(c_BB^{-1}\)有两重含义：

• 通过限制主问题求得的影子价格
• 通过限制主问题求得的对偶变量

对偶问题和原问题有同样的最优解，将原问题进行对偶，可以把原问题的变量转化为约束、约束转化为变量，因此，对于变量很多的问题将其转化为对偶问题可以很容易得到其子问题。

对偶问题

\[max \sum_{i \in I} d_i v_i \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\sum_{i in \ I} a_{ij} v_i \le 1 \qquad \qquad \forall j \in \Omega_j \\
v_j \ge 0 \qquad \qquad \qquad \quad
\forall i \in I \]

对偶问题用于推导子问题。可以进入主问题的列，就是检验数为负数的列，对于对偶问题，就是违反了约束的列。对偶问题中只有一个约束，\(\sum_{i in \ I} a_{ij} \lambda_i \le 1\)可以写成\(1-\sum_{i \in I} a_i \lambda_i \ge 0\)，求其最小值，如果最小值小于0，则说明其违反了约束。子问题用于生成新的切割方案(列)，子问题的约束对应切割约束。

子问题

\[min \quad 1-\sum_{i \in I} a_i v_i \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\sum_{i \in I} a_i l_i \le L \qquad \forall i \in I \\
a_i \ge 0 \qquad \quad \quad \forall i \in I \]

数据带入模型

以下所有的求解都可以用CPLEX进行求解，直接用CPLEX IDE实现

1. 启发式获得初始切割方案

首先有可行的切割方案才能构造出主问题，因此可以用启发式先计算出一些可行的切割方案，用于构造主问题。很简单的，每根钢管只生产一种产品，可以得到三种切割方案

切割方案	3m	6m	7m
1	5	0	0
2	0	2	0
3	0	0	2

2.开始列生成迭代

第1次迭代

松弛限制主问题：

\[min \quad x_1 + x_2 + x_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\quad\quad\quad5x_1 \qquad \qquad \quad \ge 25 \\
\quad\quad\quad\qquad 2x_2 \qquad \quad \ge 20 \\
\quad\quad\quad\qquad \qquad 2x_3 \quad\ge 18 \\
\quad\quad\quad x_1,\quad x_2,\quad x_3 \quad \ge 0 \]

对偶问题：

\[max \quad 25 v_1 + 20 v_2 + 18v_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\qquad \quad 5v_1 \qquad \qquad \qquad \quad\le 1 \\
\qquad \quad\qquad \quad 2v_2 \qquad \quad \quad\le 1 \\
\qquad \quad\qquad \qquad \qquad 2v_3\quad \le 1 \\
\quad\quad \quad v_1,\quad \quad v_2,\quad \quad v_3 \quad \ge 0 \]

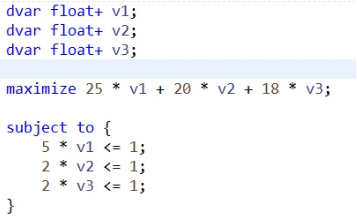
求得对偶变量的值，将其带入到子问题中

子问题：

\[min \quad 1-0.2a_1-0.5a_2-0.5a_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\quad\quad\quad 3a_1+6a_2+7a_3 \le 16\\
\quad\quad\quad a_1, \quad a_2, \quad a_3 \quad \ge 0 \]

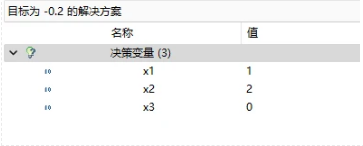
目标函数值为-0.2<0，可以加入到主问题中继续求解，新加入的一列是\(a_4=[1,2,0]^T\)，表示这个方案中一根钢管切出一根3m和2根6米

第2次迭代

松弛限制主问题：

\[min \quad x_1 + x_2 + x_3 + x_4 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\quad\quad\quad5x_1 \qquad \qquad \quad + x_4 \quad\ge 25 \\
\quad\quad\quad\qquad 2x_2 \qquad \quad + 2x_4 \ge 20 \\
\quad\quad\quad\qquad \qquad 2x_3 \quad \quad\quad\quad\ge 18 \\
\quad\quad\quad x_1,\quad x_2,\quad x_3, \quad x_4 \quad \ge 0 \]

对偶问题：

\[max \quad 25 v_1 + 20 v_2 + 18v_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\qquad \quad 5v_1 \qquad \qquad \qquad \quad\le 1 \\
\qquad \quad\qquad \quad 2v_2 \qquad \quad \quad\le 1 \\
\qquad \quad\qquad \qquad \qquad 2v_3\quad \le 1 \\
\qquad \quad v_1\quad+2v_2 \quad\quad\quad\quad\le 1 \\
\quad\quad \quad v_1, \qquad v_2, \qquad v_3 \quad \ge 0 \]

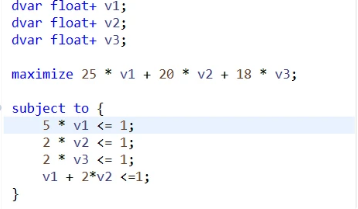
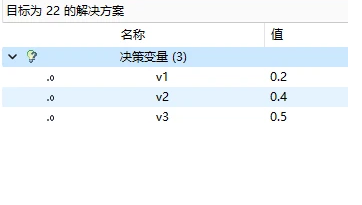
求得对偶变量的值，将其带入到子问题中

子问题：

\[min \quad 1-0.2a_1-0.4a_2-0.5a_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\quad\quad\quad 3a_1+6a_2+7a_3 \le 16\\
\quad\quad\quad a_1, \quad a_2, \quad a_3 \quad \ge 0 \]

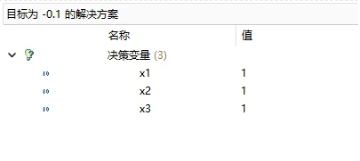
目标函数值为-0.1<0，可以加入到主问题中继续求解，可以加入到主问题中继续求解，新加入的一列是\(a_4=[1,1,1]^T\)，表示这个方案中一根钢管切出1根3m，1根6米，1根7米

第3次迭代

松弛限制主问题：

\[min \quad x_1 + x_2 + x_3 + x_4 + x_5\\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\quad\quad\quad5x_1 \qquad \qquad \quad + x_4 \quad + x_5\ge 25 \\
\quad\quad\quad\qquad 2x_2 \qquad \quad + 2x_4 +x_5\ge 20 \\
\quad\quad\quad\qquad \qquad 2x_3 \quad \quad\quad\quad +x_5\ge 18 \\
\quad\quad x_1,\quad x_2,\quad x_3, \quad x_4, \quad x_5 \quad\quad\ge 0 \]

对偶问题：

\[max \quad 25 v_1 + 20 v_2 + 18v_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\qquad \quad 5v_1 \qquad \qquad \qquad \quad\le 1 \\
\qquad \quad\qquad \quad 2v_2 \qquad \quad \quad\le 1 \\
\qquad \quad\qquad \qquad \qquad 2v_3\quad \le 1 \\
\qquad \quad v_1\quad+2v_2 \quad\quad\quad\quad\le 1 \\
\qquad \quad v_1\quad+v_2\quad+v_3 \quad\le 1 \\
\quad\quad \quad v_1, \qquad v_2, \qquad v_3 \quad \ge 0 \]

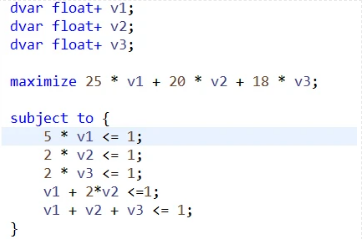
求得对偶变量的值，将其带入到子问题中

子问题:

\[min \quad 1-0.2a_1-0.4a_2-0.4a_3 \\
s.t.\qquad\qquad\qquad\qquad\qquad\\
\quad\quad\quad 3a_1+6a_2+7a_3 \le 16\\
\quad\quad\quad a_1, \quad a_2, \quad a_3 \quad \ge 0 \]

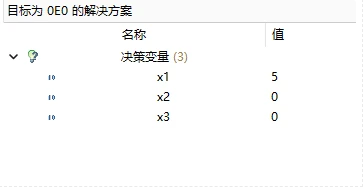
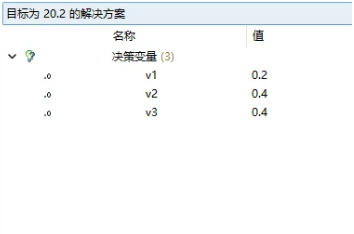
根据求解可以得到

目标值：20.2

切割方案：方案1选择1.2个；方案4选择1个，方案5选择18个

最后求得的结果包含了小数，如果想要取得整数解，需要结合分支定界算法