[CSP-S 2021] 回文

题目描述：

给定正整数 n 和整数序列 a1, a2,…,a2n，在这 2n 个数中，1, 2,…,n 分别各出现恰好 2 次。现在进行 2n 次操作，目标是创建一个长度同样为 2n 的序列 b 1,b2,…,b2n，初始时 b 为空序列，每次可以进行以下两种操作之一：

将序列 a 的开头元素加到 b 的末尾，并从 a 中移除。
将序列 a 的末尾元素加到 b 的末尾，并从 a 中移除。

我们的目的是让 b 成为一个回文数列，即令其满足对所有 1≤i≤n，有 bi=b2n+1−i。
请你判断该目的是否能达成，如果可以，请输出字典序最小的操作方案，具体在【输出格式】中说明。

输入格式：

每个测试点包含多组测试数据。

输入的第一行，包含一个整数 T，表示测试数据的组数。对于每组测试数据：

第一行，包含一个正整数 n。
第二行，包含 2n 个用空格隔开的整数 a1,a2,…,a2n 。

输出格式：

对每组测试数据输出一行答案。

如果无法生成出回文数列，输出一行 ‐1，否则输出一行一个长度为 2n 的、由字符 L 或 R 构成的字符串（不含空格），其中 L 表示移除开头元素的操作 1，R 表示操作 2。

你需要输出所有方案对应的字符串中字典序最小的一个。

字典序的比较规则如下：长度均为 2n 的字符串 s 1∼2n 比 t 1∼2n字典序小，当且仅当存在下标 1≤k≤2n 使得对于每个 1≤i<k 有 s i=t i 且 s k < t k。

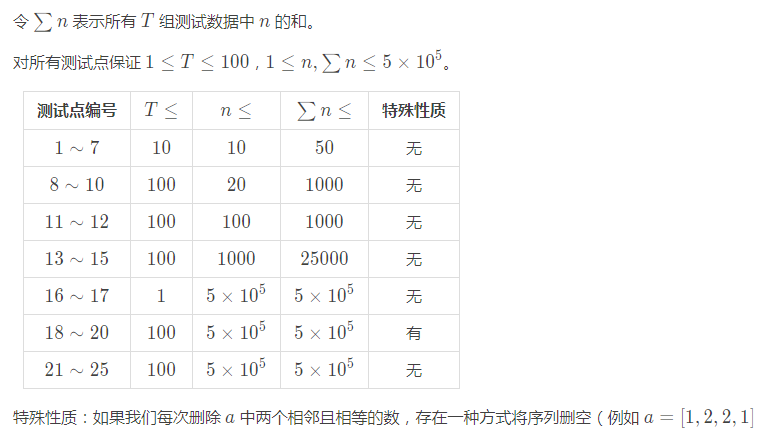
数据范围：

　　一道有趣的构造题。

　　以左端点为例分析一下：

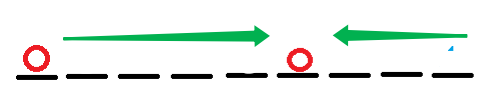
　　　　 假设红圈出数值相同，那么显然对于 左边一半 会 从左往右 取，右边一半 会 从右往左 取（如绿色箭头）。这样出来的答案是正着的。

　　　　　如果我们从中间开始往两侧去（如黄色箭头），这样出来的答案正好是 倒的。

　　　　

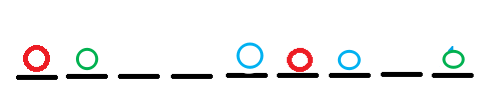
　　　　　现在我们可以取的是左右端点（即绿色点），那么，如果有解，其对应点一定位于中间点的相邻两侧（即蓝色点）。

　　想到这，就很简单了。

　　由于要字典序最小，所以优先考虑取左端点，若无解再考虑右端点，若还无解则改题无解。

　　（详见代码）

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int _,n,A[1000005],Nxt[1000005],Lst[1000005],Ans[2][500005];
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1,*p2;
inline int read()
{
    char ch;int x(0);
    while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline bool DFS(int a,int b,int c,int d)
{
    if(a>b&&c>d) return 1;
    if(a<=b)
    {
        if(a!=b&&A[a]==A[b]&&DFS(a+1,b-1,c,d)) {Ans[0][++Ans[0][0]]=1,Ans[1][++Ans[1][0]]=1;return 1;}
        if(c<=d&&A[a]==A[c]&&DFS(a+1,b,c+1,d)) {Ans[0][++Ans[0][0]]=1,Ans[1][++Ans[1][0]]=2;return 1;}
    }
    if(c<=d)
    {
        if(a<=b&&A[d]==A[b]&&DFS(a,b-1,c,d-1)) {Ans[0][++Ans[0][0]]=2,Ans[1][++Ans[1][0]]=1;return 1;}
        if(c!=d&&A[d]==A[c]&&DFS(a,b,c+1,d-1)) {Ans[0][++Ans[0][0]]=2,Ans[1][++Ans[1][0]]=2;return 1;}
    }
    return 0;
}
inline void Print(int x)
{
    if(x==1) printf("L");
    else printf("R");
    for(register int i=Ans[0][0];i;--i)
        if(Ans[0][i]==1) printf("L") ;
        else printf("R");
    for(register int i=1;i<=Ans[1][0];++i)
        if(Ans[1][i]==1) printf("L");
        else printf("R");
    printf("L\n");
}
int main()
{
    _=read();
    for(register int __=1;__<=_;++__)
    {
        n=read();for(register int i=1;i<=n;++i) Nxt[i]=Lst[i]=0;Ans[0][0]=Ans[1][0]=0,n*=2;
        for(register int i=1;i<=n;++i)
        {
            A[i]=read();
            if(Nxt[A[i]]) Lst[A[i]]=i;
            else Nxt[A[i]]=i;
        }
        if(DFS(2,Lst[A[1]]-1,Lst[A[1]]+1,n)) Print(1);
        else if(DFS(1,Nxt[A[n]]-1,Nxt[A[n]]+1,n-1)) Print(2);
        else printf("-1\n");
    }
    return 0;
}

回文