剑指 Offer 68 - II. 二叉树的最近公共祖先

剑指 Offer 68 - II. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

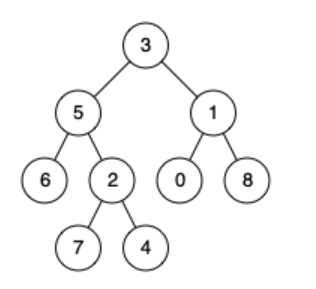
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

递归思想

算法流程：

1.终止条件：

• 如果root树根节点为空或者越节点，直接返回空
• 如果root等于p、q，则返回root

2.递归条件：

• 开启递归左节点，返回left
• 递归右节点同理

3.返回值

当left和right都不为空的时候，说明left和right在root节点异端，直接返回root即为二叉树最近的公共祖先

当left为空，则直接返回right，说明有可能p，q有一个在右节点树

当right为空，则直接返回left，同上理

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null)        return null;
        if(root.val == p.val || root.val == q.val)  return root;

        TreeNode findLeft = lowestCommonAncestor(root.left, p, q);
        TreeNode findRight = lowestCommonAncestor(root.right, p, q);

        if(findLeft != null && findRight != null)
            return root;
        else if(findLeft == null)
            return findRight;
        else
            return findLeft;
    }
}

以下代码是k神更为简洁易懂的代码：情况 1. , 2. , 3. , 4. 的展开写法如下。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null && right == null) return null; // 1.
        if(left == null) return right; // 3.
        if(right == null) return left; // 4.
        return root; // 2. if(left != null and right != null)
    }
}

参考链接：

https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/mian-shi-ti-68-ii-er-cha-shu-de-zui-jin-gong-gon-7/