联邦学习：按Dirichlet分布划分Non-IID样本

我们在《Python中的随机采样和概率分布(二)》介绍了如何用Python现有的库对一个概率分布进行采样，其中的dirichlet分布大家一定不会感到陌生。该分布的概率密度函数为

\[P(\bm{x}; \bm{\alpha}) \propto \prod_{i=1}^{k} x_{i}^{\alpha_{i}-1} \\
\bm{x}=(x_1,x_2,...,x_k),\quad x_i > 0 , \quad \sum_{i=1}^k x_i = 1\\
\bm{\alpha} = (\alpha_1,\alpha_2,..., \alpha_k). \quad \alpha_i > 0
\]

其中\(\bm{\alpha}\)为参数。

我们在联邦学习中，经常会假设不同client间的数据集不满足独立同分布(non-iid)。那么我们如何将一个现有的数据集按照non-iid划分呢？我们知道带标签样本的生成分布看可以表示为\(p(\bm{x}, y)\)，我们进一步将其写作\(p(\bm{x}, y)=p(\bm{x}|y)p(y)\)。其中如果要估计\(p(\bm{x}|y)\)的计算开销非常大，但估计\(p(y)\)的计算开销就很小。所有我们按照样本的标签分布来对样本进行non-iid划分是一个非常高效、简便的做法。

总而言之，我们采取的算法思路是尽量让每个client上的样本标签分布不同。我们设有\(K\)个类别标签，\(N\)个client，每个类别标签的样本需要按照不同的比例划分在不同的client上。我们设矩阵\(\bm{X}\in \mathbb{R}^{K*N}\)为类别标签分布矩阵，其行向量\(\bm{x}_k\in \mathbb{R}^N\)表示类别\(k\)在不同client上的概率分布向量（每一维表示\(k\)类别的样本划分到不同client上的比例)，该随机向量就采样自dirichlet分布。

据此，我们可以写出以下的划分算法：

import numpy as np
np.random.seed(42)
def split_noniid(train_labels, alpha, n_clients):
    '''
    参数为alpha的dirichlet分布将数据索引划分为n_clients个子集
    '''
    n_classes = train_labels.max()+1
    label_distribution = np.random.dirichlet([alpha]*n_clients, n_classes)
    # (K, N)的类别标签分布矩阵X，记录每个client占有每个类别的多少

    class_idcs = [np.argwhere(train_labels==y).flatten()
           for y in range(n_classes)]
    # 记录每个K个类别对应的样本下标

    client_idcs = [[] for _ in range(n_clients)]
    # 记录N个client分别对应样本集合的索引
    for c, fracs in zip(class_idcs, label_distribution):
        # np.split按照比例将类别为k的样本划分为了N个子集
        # for i, idcs 为遍历第i个client对应样本集合的索引
        for i, idcs in enumerate(np.split(c, (np.cumsum(fracs)[:-1]*len(c)).astype(int))):
            client_idcs[i] += [idcs]

    client_idcs = [np.concatenate(idcs) for idcs in client_idcs]

    return client_idcs

加下来我们在EMNIST数据集上调用该函数进行测试，并进行可视化呈现。我们设client数量\(N=10\)，dirichlet概率分布的参数向量\(\bm{\alpha}\)满足\(\alpha_i=1.0,\space i=1,2,...N\)：

import torch
from torchvision import datasets
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(42)

if __name__ == "__main__":

    N_CLIENTS = 10
    DIRICHLET_ALPHA = 1.0

    train_data = datasets.EMNIST(root=".", split="byclass", download=True, train=True)
    test_data = datasets.EMNIST(root=".", split="byclass", download=True, train=False)
    n_channels = 1

    input_sz, num_cls = train_data.data[0].shape[0],  len(train_data.classes)

    train_labels = np.array(train_data.targets)

    # 我们让每个client不同label的样本数量不同，以此做到non-iid划分
    client_idcs = split_noniid(train_labels, alpha=DIRICHLET_ALPHA, n_clients=N_CLIENTS)

    # 展示不同client的不同label的数据分布
    plt.figure(figsize=(20,3))
    plt.hist([train_labels[idc]for idc in client_idcs], stacked=True,
            bins=np.arange(min(train_labels)-0.5, max(train_labels) + 1.5, 1),
            label=["Client {}".format(i) for i in range(N_CLIENTS)], rwidth=0.5)
    plt.xticks(np.arange(num_cls), train_data.classes)
    plt.legend()
    plt.show()

最终的可视化结果如下：



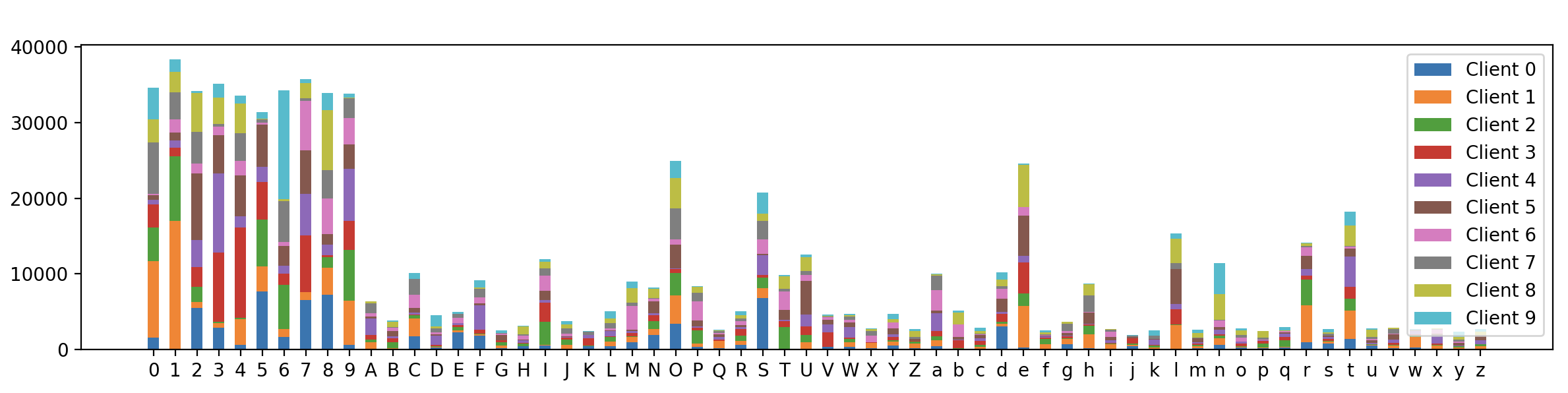
可以看到，62个类别标签在不同client上的分布确实不同，证明我们的样本划分算法是有效的。