Polya 定理 学习笔记

群

群的定义

我们定义，对于一个集合 \(G\) 以及二元运算 \(\times\)，如果满足以下四种性质，那我们就称 \((G,\times)\) 为一个群。

1. 封闭性

对于 \(a\in G,b\in G\)，那么有 \(a\times b\in G\)

2. 结合律

\(a\times (b\times c)=(a\times b)\times c\)

似乎这个东西没有什么用蛤？

3. 单位元

存在一个元素 \(e\in G\)，使得任意 \(a\in G\) 有 \(a\times e=e\times a=a\) 。我们称 \(e\) 为 \(G\) 的单位元。

可以证明，对于一个群单位元是唯一的。假设存在两个单位元 \(e_1,e_2\)，那么 \(e_1\times e_2=e_1\) 并且 \(e_1\times e_2=e_2\)，由此推出矛盾。

4. 逆元

\(\forall a\in G,\exists a^{'} \in G \wedge a\times a^{'}=a^{'}\times a=e\)。可以证明，对于一个 \(a\)，\(a^{'}\) 是唯一的。

假设存在 \(a_1,a_2\) 都是 \(a\) 的逆元。那么就有 \((a_1\times a)\times a_2=a_2,a_1\times (a\times a_2)=a_1\)，二者矛盾。

子群的定义

对于一个群 \((G,\times )\)，如果存在 \(H\subseteq G\)，且 \((H,\times )\) 构成一个群，那我们就称 \(H\) 为 \(G\) 的一个子群，简记为 \(H\leq G\)。

对于 \(g\in G\)，我们称 \(gH=\{x|x=g\times h,h\in H\}\) 为 \(H\) 在 \(G\) 内关于 \(g\) 的左陪集。\(Hg=\{x|x=h\times g,g\in H\}\) 为 \(H\) 在 \(G\) 内关于 \(g\) 的右陪集。

下面有一些关于陪集的性质，为了方便，我们在此仅讨论右陪集的性质，左陪集同理可证。

1. \(\forall g\in G,|H|=|Hg|\)

可以看出，如果存在 \(h_1\times g=h_2\times g\) 且 \(h_1\not= h_2\)，因为逆元是唯一的，所以我们二者都乘上 \(g^{'}\) 即可证明矛盾。

1. \(\forall g\in G,g\in Hg\)

因为 \(e\in G\)，所以证毕。

1. \(Hg=H\Longleftrightarrow g\in H\)

根据群的封闭性可以得证。

1. \(Ha=Hb\Longleftrightarrow a\times b^{-1}\in H\)

如果有 \(Ha=Hb\)，那么就有 \(Ha\times b^{-1}=H\)，那么由第三个性质就可以推出 \(a\times b^{-1}\in H\)。逆命题同理。

1. \(Ha\cap Hb\not=\emptyset \Rightarrow Ha=Hb\)

我们假设存在 \(h_1,h_2\in H\)，使得 \(h_1\times a=h_2\times b=c\)，所以我们可以得到 \(h_1\times h_2^{-1}=b\times a^{-1}\)，又因为 \(h_1,h_2^{-1}\in H\rightarrow h_1\times h_2^{-1}\in H\)，所以 \(b\times a^{-1}\in H\)，所以 \(Ha=Hb\)。

1. \(H\) 所有右陪集的并为 \(G\)

我个人觉得比较显然。

一些符号的约定

若 \(H\leq G\)，那 \(G/H\) 表示所有 \(H\) 的左陪集，即 \(\{gH,g\in G\}\)

若 \(H\leq G\)，那 \([G:H]\) 表示 \(G\) 中不同的 \(H\) 的左陪集的数量。

拉格朗日定理

对于 \(H\leq G\)，有：

\[|H|\times [G:H]=|G|
\]

证明：因为性质 \(5\) 我们知道所有本质不同的左陪集如果不是完全不相同就是完全相同，所以证毕。

置换

置换的定义

我们对于一个置换，大概长成这个样子：

\[\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 3 & 5 & 1
\end{pmatrix}
\]

我们定义其含义为第 \(2\) 元素替换第 \(1\) 个元素，第 \(4\) 个元素替换第 \(2\) 个元素。。。。。。

但是写成两行太烦了，所以我们一般默认第一行为 \(\begin{pmatrix}1&2&3&4& ... &n\end{pmatrix}\)，写成 \(\begin{pmatrix}2 & 4 & 3 & 5 & 1\end{pmatrix}\)

置换的运算

我们假设有两个置换，分别是 \(\sigma\) 和 \(a\)，那么我们定义 \(\sigma \times a=\begin{pmatrix}a_{\sigma_1} & a_{\sigma_2} & ... & a_{\sigma_n}\end{pmatrix}\)。一般也可以写成 \(\sigma(a)\)。

置换群

置换群显然就是元素为置换的群，对于一个 \(1,2,3,...,n\)，我们定义它的置换群为所有置换的集合，共 \(n!\) 个置换。（\(\times\) 的法则同上）我们可以证明它满足群的四个基本性质。

轨道-稳定子定理

群作用

我们定义群 \(G\) 作用于集合 \(M\)，当且仅当给定的二元函数 \(\varphi(v,k),v\in G,k\in M\) 满足以下性质：

\[\left\{\begin{array}{l}
\varphi(e,k)=k\\
\varphi(s_1,\varphi(s_2,k))=\varphi(s_1\times s_2,k)
\end{array}\right.\]

轨道

对于一个作用于 \(M\) 的群 \(G\)，我们定义 \(x\in M\) 的轨道就是 \(x\) 通过 \(G\) 的元素可以转移到的元素集合，我们即为 \(G(x)\)，我们还顺便定义 \(g(x)\) 表示 \(x\) 通过 \(g\) 转移到的元素，即 \(g(x)=\varphi(g,x)\)。

稳定子

我们定义 \(G^x=\{g|g(x)=x,g\in G\}\) 。

轨道-稳定子定理

\[|G^x|\times |G(x)|=|G|
\]

---

证明：我们首先可以说明 \(G^x\) 是 \(G\) 的一个子群。结合律和单位根不会变。考虑证明封闭性，假设有 \(f\in G^x,g\in G^x,f(x)=g(x)=x\)，那么由群作用有 \((f\times g)(x)=x\)，所以证毕。考虑证明逆元性，对于一个元素 \(g\in G^x\)，那么有 \((g\times g^{'})(x)=e(x)=x\)，所以 \(g^{'}\in G^x\)。

那么，我们根据拉格朗日定理就有 \(|G^x|\times [G:G^x]=|G|\)，也就是说，我们现在只需要证明 \([G:G^x]=|G(x)|\)。也就是说，每一个 \(g(x)\) 都可以找到对应的 \(G^x\) 在 \(G\) 中的一个陪集。

我们假设存在 \(f(x)=g(x),f,g\in G,f\not=g\)，因为 \((f\times g^{-1})(x)=x=e(x)\in G^x\)，则 \(fG^x=gG^x\)。那我们就说明了相同的 \(f(x)\) 总是对应相同的陪集。

那我们也可以反过来说明相同的陪集总是对应相同的 \(f(x)\)。

我们就这样证明了。

Burnside 定理

定义元素 \(x,y\in M\) 是等价类当且仅当存在 \(f\in G\) 使得 \(f(x)=y\)，定义 \(|M/G|\) 表示 \(M\) 集合中在 \(G\) 的作用下不同的等价类的个数。Burnside 定理告诉我们：

\[|M/G|=\frac{1}{|G|}\sum_{g\in G} M^g
\]

其中 \(M^g\) 表示 \(M\) 中满足 \(g(x)=x\) 的个数。

---

证明：

\[\sum_{g\in G} |M^g|=\sum_{x\in M} |G^x|
\]

\[=\sum_{x\in M} \frac{|G|}{|G(x)|} \text{(由轨道-稳定子定理可得)}
\]

\[=|G|\sum_{x\in M} \frac{1}{|G(x)|}
\]

\[=|G|\sum_{Y\in M/G} \sum_{x\in Y} \frac{1}{|G(x)|}
\]

\[=|G|\sum_{Y\in M/G} \sum_{x\in Y} \frac{1}{|Y|}
\]

\[=|G||M/G|
\]

所以，我们就推出了 \(\text{Burnside}\) 定理：

\[|M/G|=\frac{1}{|G|}\sum_{g\in G} |M^g|
\]

Polya 定理

似乎有了 Burnside 定理，Polya 定理就很好推了。

Polya 定理一般都是用于置换群，我们假设 \(c(g)\) 表示在 \(g\) 这个置换中，\(i\to g_{i}\) 连边的图中的环的个数，那么，Burnside 就可以改写为：

\[|M/G|=\frac{1}{|G|}\sum_{g\in G}m^{c(g)}
\]

其中 \(m\) 是可以填的颜色个数。

Some Problems

SP419 Transposing is Fun

题目传送门

Description

给出一个 \(2^a\times 2^b\) 的矩阵，你要把它弄成它的转置矩阵，而且还得保持 \(2^a\times 2^b\) 的形状。问交换次数。

有 \(T(T\le 100)\) 次查询，每次给出的 \(a,b\) 满足 \(0\le a+b\le 5\times 10^5\)

Solution

这个题确实很有意思的。

我们首先可以想到，最后的结果就是一个置换。举个例子，假设我们一开始的矩阵长成这样：

那么，它的转置矩阵就长成这样：

可以看出，它的置换就是：

\[\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\
1 & 5 & 2 & 6 & 3 & 7 & 4 & 8
\end{pmatrix}
\]

我们发现，实际上这就有四个环：\((1)(2,5,3)(4,6,7)(8)\)。可以看出，假设有 \(k\) 个环，那么，答案就是：

\[2^{a+b}-k
\]

因为假设一个环的大小为 \(m\)，那么我们只需要交换只需要 \(m-1\) 就可以刚好轮换一圈。

问题就是怎么求 \(k\)。我们可以发现的规律是，对于一个环里面的点，它编号减一多次进行往右移动 \(a\) 位那么结果都一样（是项链的移动，长度是 \(a+b\) 位）。这个是可以证明的，这里就不赘述了。

于是，问题就变成了，一个长度为 \(a+b\) 的项链，每个点可以染黑白两色，两个项链如果可以通过多次向右移动 \(a\) 位变得一样，认为它们是本质相同的元素。问不同的本价类个数。

这个就比较可以 Polya 做了。因为我们知道如果移动 \(k\) 步，那么有 \(\gcd(k,n)\) 个循环节，所以我们直接 Polya 定理上，答案就是：

\[\frac{1}{n}\sum_{k=1}^{n} 2^{\gcd(ka,a+b)},n=(a+b)/\gcd(a,b)
\]

可以证明，这个东西和：

\[\frac{1}{n}\sum_{k=1}^{n} 2^{\gcd(a,b)\times \gcd(k,n)},n=(a+b)/\gcd(a,b)
\]

是等价的。所以我们使用一些套路的莫比乌斯反演技巧，就可以得到答案等于：

\[\frac{1}{n}\sum_{d|n} x^d\varphi(n/d),x=2^{\gcd(a,b)},n=(a+b)/\gcd(a,b)
\]

Code

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define mod 1000003
#define MAXN 500005

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int gcd (int a,int b){return !b ? a : gcd (b,a % b);}
int lcm (int a,int b){return a / gcd (a,b) * b;}
int mul (int a,int b){return 1ll * a * b % mod;}
int dec (int a,int b){return a >= b ? a - b : a + mod - b;}
int add (int a,int b){return a + b >= mod ? a + b - mod : a + b;}
int qkpow (int a,int b){
	int res = 1;for (;b;b >>= 1,a = mul (a,a)) if (b & 1) res = mul (res,a);
	return res;
}

bool vis[MAXN];
int tot,pw[MAXN],prime[MAXN];

void Euler (int up){
	pw[0] = 1;
	for (Int i = 1;i <= up;++ i) pw[i] = mul (pw[i - 1],2);
	for (Int i = 2;i <= up;++ i){
		if (!vis[i]) prime[++ tot] = i;
		for (Int j = 1;j <= tot && i * prime[j] <= up;++ j){
			vis[i * prime[j]] = 1;
			if (i % prime[j] == 0) break;
		}
	}
}

int n,x,cnt,ans,pri[MAXN],zhi[MAXN];
void Add (int &a,int b){a = add (a,b);}

void dfs (int now,int getp,int getv){
	if (now > cnt) return Add (ans,mul (getp,pw[x * n / getv]));
	dfs (now + 1,getp,getv);
	for (Int i = 1,v = pri[now];i <= zhi[now];++ i,v *= pri[now])
		dfs (now + 1,getp * v / pri[now] * (pri[now] - 1),getv * v);
}

int Work (int a,int b){
	ans = 0,n = (a + b) / gcd (a,b),x = gcd (a,b),cnt = 0;int tmpn = n;
	for (Int i = 1;i <= tot && prime[i] * prime[i] <= n;++ i) if (n % prime[i] == 0){
		pri[++ cnt] = prime[i],zhi[cnt] = 0;
		while (n % prime[i] == 0) n /= prime[i],zhi[cnt] ++;
	}
	if (n > 1) pri[++ cnt] = n,zhi[cnt] = 1;n = tmpn;dfs (1,1,1);
	return dec (qkpow (2,a + b),mul (ans,qkpow (n,mod - 2)));
}

signed main(){
	Euler (5e5);int T;read (T);
	for (Int i = 1,a,b;i <= T;++ i) read (a,b),write (Work (a,b)),putchar ('\n');
    return 0;
}

[HNOI2009]图的同构计数

题目传送门

Description

给出 \(n\) ，给出点集大小为 \(n\) 的无向图的等价类个数。定义两个图是同构的当且仅当可以通过改变置换点的编号得到另一个图。

\(n\le 60\)

Solution

湖南 OIer 真的太惨了！！！（还好我不是

首先可以想到的是，这个图不存在的可以用 \(0\) 表示，存在的边用 \(1\) 表示，那么就相当于用 \(2\) 种颜色给大小为 \(n\) 的完全图染色，问等价类个数。

我们可以发现，我们真正关键的就是对于一个点置换，边的循环个数。我们可以分两种情况进行讨论。

---

1. 这条边的两个端点在点置换中是一个循环里面的

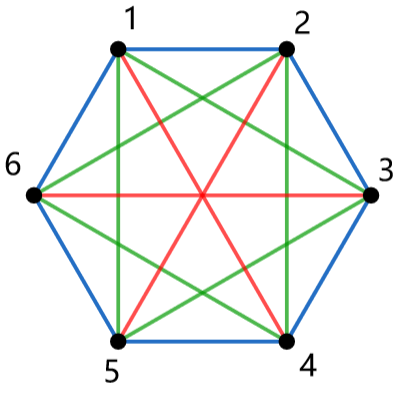
可以看出，在这个长度为 \(6\) 的循环里面，等价的边都是长度相等的边，这个也可以说明，毕竟你每次相当于整体旋转一格，边的长度不会变。

所以，长度为 \(b\) 的点循环里面，边循环有 \(\lfloor\frac{b}{2}\rfloor\) 个。

---

1. 两个端点不在一个点循环里面

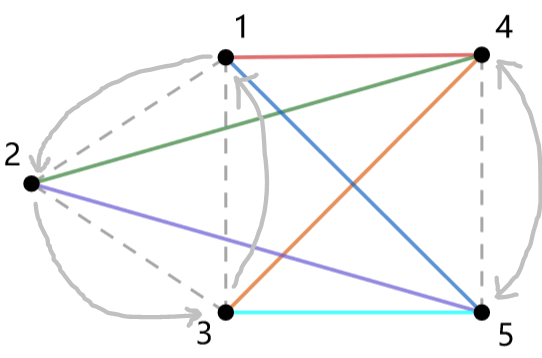
可以看出，假设两个所属点循环大小为 \(b_1,b_2\)，那么，只有点置换执行 \(\text{lcm}(b_1,b_2)\) 这个边会回到原处，所以每个循环大小为 \(\text{lcm}(b_1,b_2)\)，一共 \(b_1\times b_2\) 条边，那就有 \(\gcd(b_1,b_2)\) 个循环。

---

所以，假设点循环的大小为 \(b_1,b_2,...,b_m\)，那么，边循环就有：

\[\sum_{i=1}^{m} \lfloor\frac{b_i}{2}\rfloor+\sum_{i=1}^{m}\sum_{j=1}^{i-1}\gcd(b_i,b_j)
\]

但是一共 \(n!\) 个置换，你不可能一个一个地枚，所以我们肯定只有枚举 \(b_1,b_2,...,b_m\) ，然后算出对于每一个这种情况有多少个置换对应。

首先你需要给每个循环选元素，那么这部分就是：

\[\binom{n}{b_1}\binom{n-b_1}{b_2}\binom{n-b_1-b_2}{b_3}...\binom{b_m}{b_m}
\]

可以看出，这就等价于 \(\frac{n!}{\prod_{i=1}^{m} b_i!}\)。同时，每个循环里面还可以排列，个数为 \((b_i-1)!\)。所以是 \(\frac{n!}{\prod_{i=1}^{m} b_i}\)。但是这样会算重，因为大小相同的循环你不同的排列方法会对应相同的置换，对于大小为 \(i\) 的循环来说，会算重 \(c_i!\) 次，\(c_i\) 等于大小为 \(i\) 的循环个数。所以答案其实就是：

\[\frac{n!}{\prod_{i=1}^{m} b_i\prod_{i=1}^{n} c_i!}
\]

那么，根据 Polya 定理，我们就可以得到答案：

\[\frac{1}{n!}\sum_{b_1,b_2,...,b_m} 2^{k}\times \frac{n!}{\prod_{i=1}^{m} b_i\prod_{i=1}^{n} c_i!},k=\sum_{i=1}^{m} \lfloor\frac{b_i}{2}\rfloor+\sum_{i=1}^{m}\sum_{j=1}^{i-1}\gcd(b_i,b_j)
\]

\(60\) 的整数拆分方案数应该不会很大吧。。。

Code

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define MAXN 65
#define mod 997

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int n;
int gcd (int a,int b){return !b ? a : gcd (b,a % b);}
int lcm (int a,int b){return a / gcd (a,b) * b;}
int mul (int a,int b){return 1ll * a * b % mod;}
int dec (int a,int b){return a >= b ? a - b : a + mod - b;}
int add (int a,int b){return a + b >= mod ? a + b - mod : a + b;}
int qkpow (int a,int b){
	int res = 1;for (;b;b >>= 1,a = mul (a,a)) if (b & 1) res = mul (res,a);
	return res;
}

int ans,b[MAXN],c[MAXN],fac[MAXN];
void Add (int &a,int b){a = add (a,b);}

void getK (int up){
	int res = 0,v = 1;
	for (Int i = 1;i <= up;++ i) res += b[i] / 2,v = mul (v,b[i]);
	for (Int i = 1;i <= up;++ i) for (Int j = 1;j < i;++ j) res += gcd (b[i],b[j]);
	res = qkpow (2,res);
	for (Int i = 1;i <= b[up];++ i) v = mul (v,fac[c[i]]);
	Add (ans,mul (res,qkpow (v,mod - 2)));
}

void dfs (int now,int sum,int las){
	if (n - sum < las) return ;
	b[now] = n - sum,c[b[now]] ++,getK (now),c[b[now]] --;
	for (Int i = las;i < n - sum;++ i) b[now] = i,c[i] ++,dfs (now + 1,sum + i,i),c[i] --;
}

signed main(){
	read (n),fac[0] = 1;
	for (Int i = 1;i <= n;++ i) fac[i] = mul (fac[i - 1],i);
	dfs (1,0,1),write (ans),putchar ('\n');
    return 0;
}