【风控算法】一、变量分箱、WOE和IV值计算

一、变量分箱

变量分箱常见于逻辑回归评分卡的制作中，在入模前，需要对原始变量值通过分箱映射成woe值。举例来说，如“年龄”这一变量，我们需要找到合适的切分点，将连续的年龄打散到不同的”箱“中，并按年龄落入的“箱”对变量进行编码。

关于变量分箱的作用，相关资料中的解释有很多，我认为变量分箱最主要有三个作用：

1. 归一化：分箱且woe编码映射后的变量，可以将变量归一到近似尺度上；
2. 引入非线性：对于逻辑回归这类线性模型，引入变量分箱可以增强模型的拟合能力；
3. 增强鲁棒性：分箱可以避免异常数据对模型的影响

二、IV值和WOE

（1）WOE

WOE(Weight of Evidence)，是一种对变量编码的形式。通过对分箱后每一箱WOE值的计算，可以完成变量从原始数值->WOE数值的映射。

\[WOE_i = ln(\frac{y^1_i/y^1}{y^0_i/y^0})=ln(\frac{y^1_i/y^0_i}{y^1/y^0})
=ln(\frac{y^1_i}{y^1})-ln(\frac{y^0_i}{y^0})=ln(\frac{y^1_i}{y^0_i})-ln(\frac{y^1}{y^0})
\]

关于WOE的理解，主要有如下几点：

1. WOE可以理解成分箱区间内的正负样本差异相对于整体的差异。机器学习二分类中，通常将分类任务中更关注的类label设为”1“，因此WOE越大说明该分箱内的样本越可能为“1”类；
2. 经过WOE编码，实现了按WOE排序的区间正样本比例呈单调趋势。

（2）IV值

IV(Information Value)是基于WOE计算来的：

\[IV = \sum WOE_i*(\frac{y_i^1}{y^1}-\frac{y_i^0}{y^0})
\]

（3）KL散度

KL散度（相对熵）通常用于衡量两个分布之间的差异，机器学习中，\(P\)往往代表样本的真实分布，而\(Q\)代表样本的预测分布，那么KL散度可以计算两个分布之间的差异：

\[D_{KL}(p||q) =\sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)})
\]

如果\(P\)的分布和\(Q\)的分布越接近，KL散度的值就会越小。

KL散度通常被称作KL距离，但却只满足距离的非负性和同一性，不满足对称性和直递性，因此不是严格意义上的“距离"。

设分箱后，\(y=1\)的分布为\(p_1(x)\),\(y=0\)的分布为\(p_0(x)\)，那么

\[\begin{aligned}
KL(p_0,p_1)+KL(p_1,p_0)
&= \sum p(x_i)*log(\frac{p(x_i)}{q(x_i)})+\sum q(x_i)*log(\frac{q(x_i)}{p(x_i)})\\
&=\sum{(p(x_i)-q(x_i))*(log(p(x_i))-log(q(x_i)))}\\
&= IV
\end{aligned}
\]

由此可知，\(IV=KL(p_0,p_1)+KL(p_1,p_0)\)

据此可以得到关于IV和KL散度更加深刻的理解：

• IV值衡量了分组下好坏样本分布差异，IV值越大分布差异越大，IV值越小分布差异越小
• IV是KL散度的一种对称化处理

三、分箱方法

变量分箱主要包括无监督方法和有监督方法，无监督的方法，在分箱中没有用到y有关的信息，而有监督的分箱方法，在分箱时引入了y的分布，运用训练集找到分箱的切点。

（1）无监督分箱

a.等频分箱/等距分箱

如字面理解，等频分箱和等距分箱可直接通过pandas的qcut和cut实现

等频分箱：qcut IV=0.0158

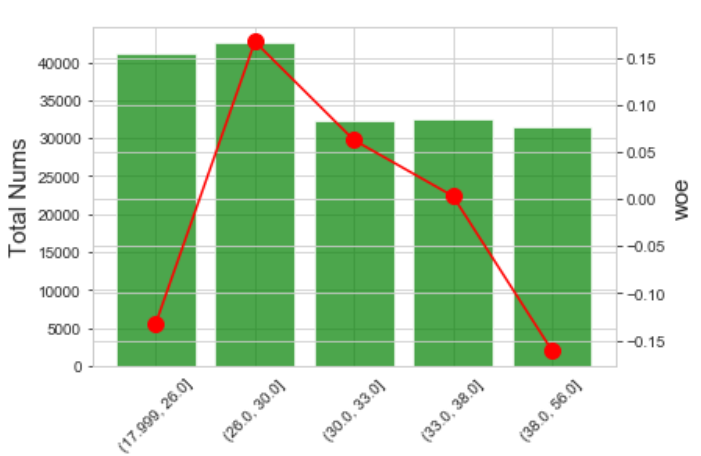
等距分箱：cut IV=0.019

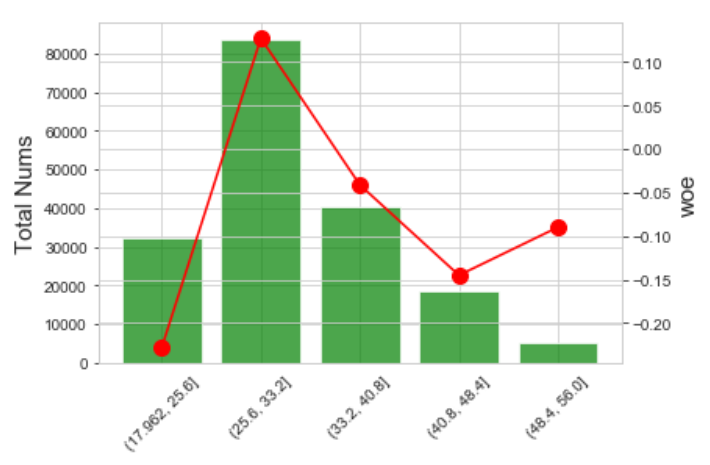
b.聚类分箱

无监督分箱中除了等频分箱和等距分箱外，也可以使用KMeans算法实现聚类分箱，一个粗糙的代码实现如下：

from sklearn.cluster import KMeans
def kmeansbin(data,x='x',bin_nums=5):
    minus_ = 999*(data[x].max() - data[x].min())
    bin_nums = 5
    clf = KMeans(n_clusters=bin_nums-1, random_state=999)
    _ = clf.fit_predict(data[[x,x]])
    cut_point = sorted(clf.cluster_centers_[:,0])
    #cut_point = [(clf_center[i]+clf_center[i+1])/2 for i in range(len(clf_center)-1)]
    return [data[x].min()-minus_,] + cut_point + [data[x].max()+minus_,]

效果如下： IV=0.0208

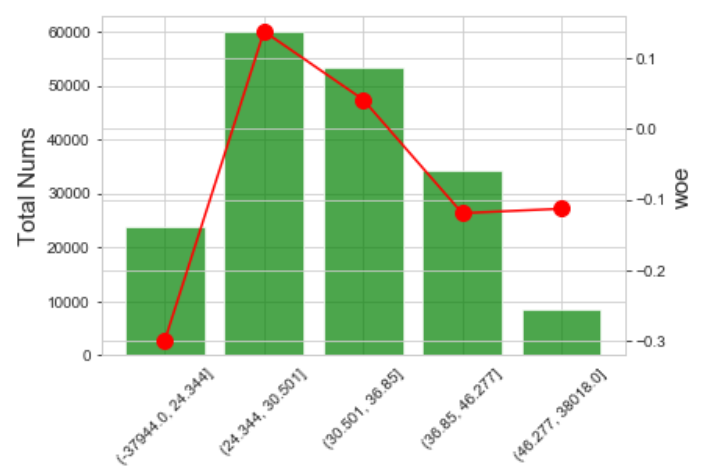
(2)有监督分箱

a.决策树分箱

决策树分箱利用单变量生成决策树，利用决策树的分裂规则完成变量分箱，因分箱速度快且效果比较稳定，同时也有sklearn接口可以调用，因此较为常用，一个简单的代码实现版本如下：

# 决策树分箱
from sklearn.tree import DecisionTreeClassifier
def treebin(df,x='x',y='y',max_leaf_nodes=5,min_samples_leaf=0.05):
    # 训练决策树
    df = df.copy()
    df[x] = df[x].fillna(-9999)
    model = DecisionTreeClassifier(criterion='entropy',max_leaf_nodes=max_leaf_nodes,min_samples_leaf=min_samples_leaf)
    model.fit(df[[x]],df[[y]])

    # 从树结构获取决策边界
    right_node = model.tree_.children_right
    left_node = model.tree_.children_left
    tree_threshold = model.tree_.threshold

    # sklearn树结构，详见：https://scikit-learn.org/stable/auto_examples/tree/plot_unveil_tree_structure.html#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py
    final_cut = [tree_threshold[i] for i,node in enumerate(zip(right_node,left_node)) if node[0]!=node[1]]
    minus_ = df[x].max() - df[x].min()
    # 返回分箱边界
    return [df[x].min()-999*minus_,]+sorted(final_cut)+[df[x].max()+999*minus_]

分箱效果如下: IV=0.0286

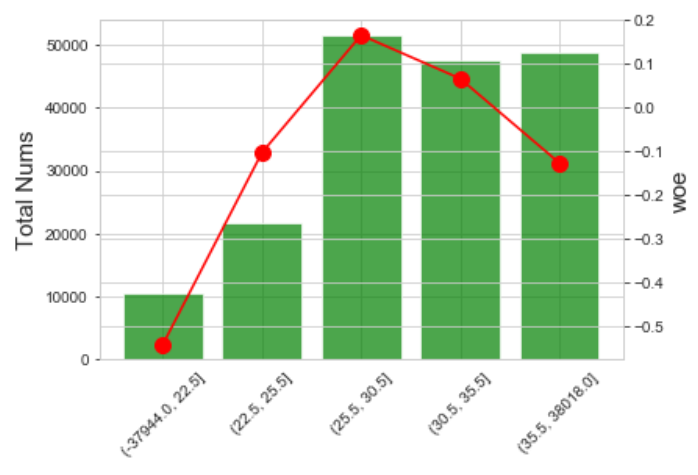
b.卡方分箱

卡方分箱通过计算变量所有不同值之间的卡方值，并对卡方值最低的区间进行合并迭代，最终达到迭代要求的剩余箱数来完成分箱，简要代码实现如下：

def chibin(data,x='x',y='y',bin_nums=5,confidenceVal=6.635):
    def cal_chi(arr):
        sum_ = np.sum(arr[:,:2])
        denom_ = np.sum(arr[0,:2])*np.sum(arr[1,:2])*np.sum(arr[:,0])*np.sum(arr[:,1])
        chi_ = (arr[0][0]*arr[1][1] - arr[0][1]*arr[1][0])**2 * sum_ / denom_
        return chi_

    # 所有不同值，计数
    total_num = data.groupby([x])[y].apply(lambda x:{'nums':x.count()}).unstack()
    # 正样本计数
    total_num['x'] = total_num.index.tolist()
    total_num['pos_nums'] = data.groupby([x])[y].sum()
    total_num['neg_nums'] = data.groupby([x])[y].apply(lambda x:x.count()-x.sum())
    total_num = total_num[['pos_nums','neg_nums','x']]
    total_num = total_num.values

    # 第一步：合并连续的全正/全负区间
    i = 0
    while i<len(total_num)-1:
        if (total_num[i][0] == total_num[i+1][0] == 0) or (total_num[i][1] == total_num[i+1][1] == 0):
            total_num[i,2] = 0
            total_num[i] += total_num[i+1]
            total_num = np.delete(total_num,i+1,axis=0)
        else:
            i += 1

    # 第二步：计算相邻区间的卡方值，并存入数组
    arr_chi = np.array([])
    for i in range(len(total_num)-1):
        arr_chi = np.append(arr_chi,cal_chi(total_num[i:i+2]))

    # 第三部：分箱合并
    while len(arr_chi)>bin_nums and min(arr_chi)<confidenceVal:
        idxmin = np.argmin(arr_chi)
        # 与下一个区间合并
        total_num[idxmin,2] = 0
        total_num[idxmin] += total_num[idxmin+1]
        total_num = np.delete(total_num,idxmin+1,axis=0)
        # 更新卡方值
        # 如果 最低卡方值是前两个区间
        # 如果 最低卡方值是最后两个区间
        # 如果 最低卡方值在中间

        if idxmin == 0:
            arr_chi[0] = cal_chi(total_num[:2])
            arr_chi = np.delete(arr_chi,1,axis=0)
        elif idxmin == len(arr_chi)-1:
            arr_chi[idxmin-1] = cal_chi(total_num[idxmin-1:])
            arr_chi = np.delete(arr_chi,idxmin,axis=0)
        else:
            arr_chi[idxmin-1] = cal_chi(total_num[idxmin-1:idxmin+1,:])
            arr_chi[idxmin+1] = cal_chi(total_num[idxmin:idxmin+2,:])
            arr_chi = np.delete(arr_chi,idxmin,axis=0)

    # 合并完毕，返回分箱边界
    minus_ = total_num[:,2].max() - total_num[:,2].min()

    return [total_num[:2].min() - 999*minus_,] + sorted(total_num[:-1,2]) + [total_num[:2].max() + 999*minus_,]

卡方值和KL散度一样，都是用于衡量分布之间差异的指标，因此处不是重点，所以不再详细说明

效果如下： IV=0.0303

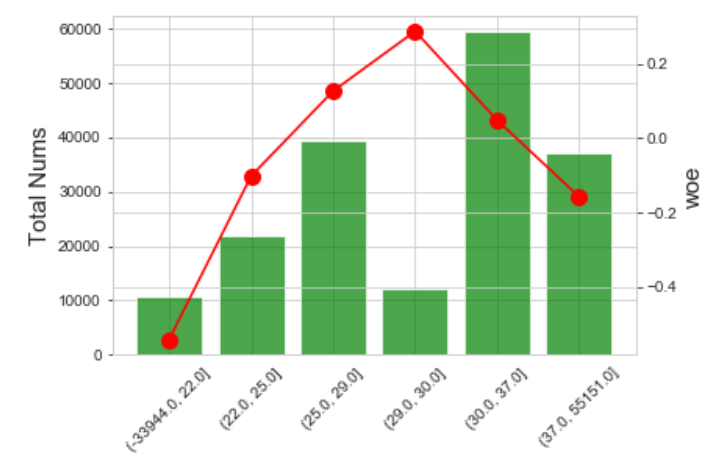
c.BestKS分箱

BestKS分箱通过不断计算所有可能切分点的KS，每次分箱选择让KS最大的切分点，最终达到要求的分箱数来完成分箱，具体的实现思路其他文章中都有较为详细的介绍，因此此处也不再赘述。

一个简要的代码实现：

def bestksbin(data,x='x',y='y',bin_nums=5,stopl=0.05):
    cut_point = []
    minus_ = 999*(data[x].max() - data[x].min())

    if len(data[x].unique())<=bin_nums:
        cut_point = data[x].unique()
        return [data[x].min()-minus_,] + cut_point + [data[x].max()+minus_,]

    cut_point.append(binks(data,x,y)[0])

    while len(cut_point) < bin_nums-1:
        bestks = -999
        bestcut = None
        icnt = 0
        while icnt <= len(cut_point):
            if icnt == 0:
                tmpcp,tmpks = binks(data[data[x]<=cut_point[icnt]],x,y,l=data.shape[0],stopl=stopl)
            elif icnt == len(cut_point):
                tmpcp,tmpks = binks(data[data[x]>cut_point[icnt-1]],x,y,l=data.shape[0],stopl=stopl)
            else:
                tmpcp,tmpks = binks(data[(data[x]>cut_point[icnt-1])&(data[x]<=cut_point[icnt])],x,y,l=data.shape[0],stopl=stopl)
            if tmpks > bestks:
                bestcut,bestks = tmpcp,tmpks
            icnt += 1
        if not bestcut:
            break
        cut_point.append(bestcut)
        cut_point = sorted(cut_point)
    return [data[x].min()-minus_,] + cut_point + [data[x].max()+minus_,]

def binks(data,x='x',y='y',l=10000,stopl=0.05):
    if (len(data[x].unique()) == 1) or (data.shape[0]/l<stopl) or (data[y].sum()==data.shape[0]) or (data[y].sum()==0):
        return None,-9999
    tmp = data.groupby(x)[y].apply(lambda x:{'count':x.count(),'bad':x.sum()}).unstack()
    tmp['x'] = tmp.index.tolist()
    tmp['good'] = tmp['count'] - tmp['bad']
    tmp['cumgood'] = tmp['good'].cumsum()
    tmp['cumbad'] = tmp['bad'].cumsum()
    tmp['cumgood_ratio'] = tmp['cumgood'] / (data.shape[0] - data['y'].sum())
    tmp['cumbad_ratio'] = tmp['cumbad'] / data['y'].sum()
    tmp['KS'] = abs(tmp['cumgood_ratio']-tmp['cumbad_ratio'])
    tmp = tmp.reset_index(drop=True)
    tmp = tmp[tmp['x'] != tmp['x'].max()]
    maxidx = tmp['KS'].argmax()
    return tmp.loc[maxidx ,'x'],tmp.loc[maxidx,'KS']

分箱效果如下： IV=0.0281

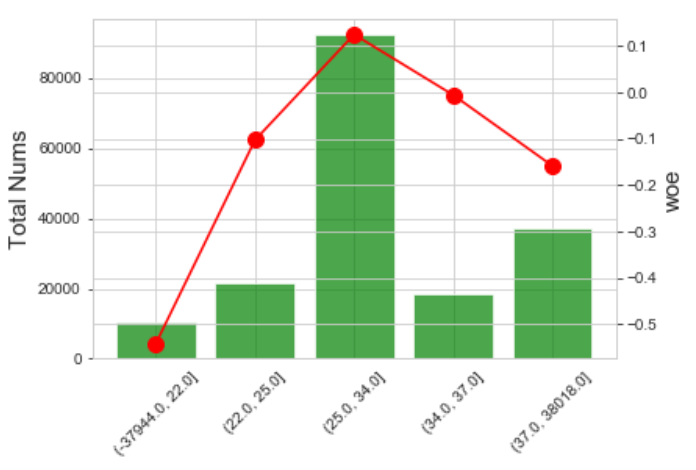
总结

本文主要记录了变量分箱、WOE和IV值计算，其中包括了有监督分箱的几种方法的代码实现，代码写的仓促可能其中有一些疏漏，在未来的学习和研究中可能会优化其中代码。

参考资料

特征工程之特征分箱

KL散度