[BUUCTF]REVERSE——[GKCTF2020]BabyDriver

[GKCTF2020]BabyDriver

附件

步骤：

1. 例行检查，64位程序，无壳
   
2. 64位ida载入，检索程序里的字符串，看到提示flag是md5（input），下方还看到了类似迷宫的字符串
   
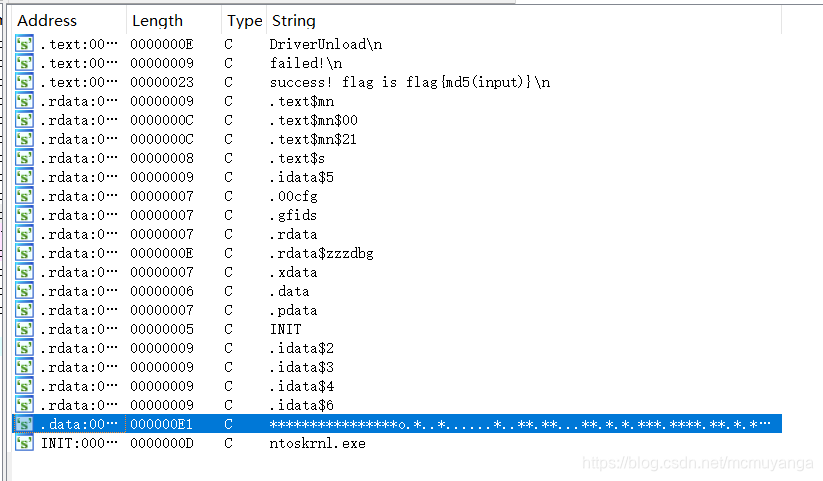
3. 找到关键函数
   
   从o出发到#结束，碰到*失败，只能走‘.’,但是这个上下左右md5加密出来的东西不对

看了别人的wp才知道这里由于是sys文件，是由键盘过滤驱动获取键盘扫描码来控制上下左右，而不是ascll码

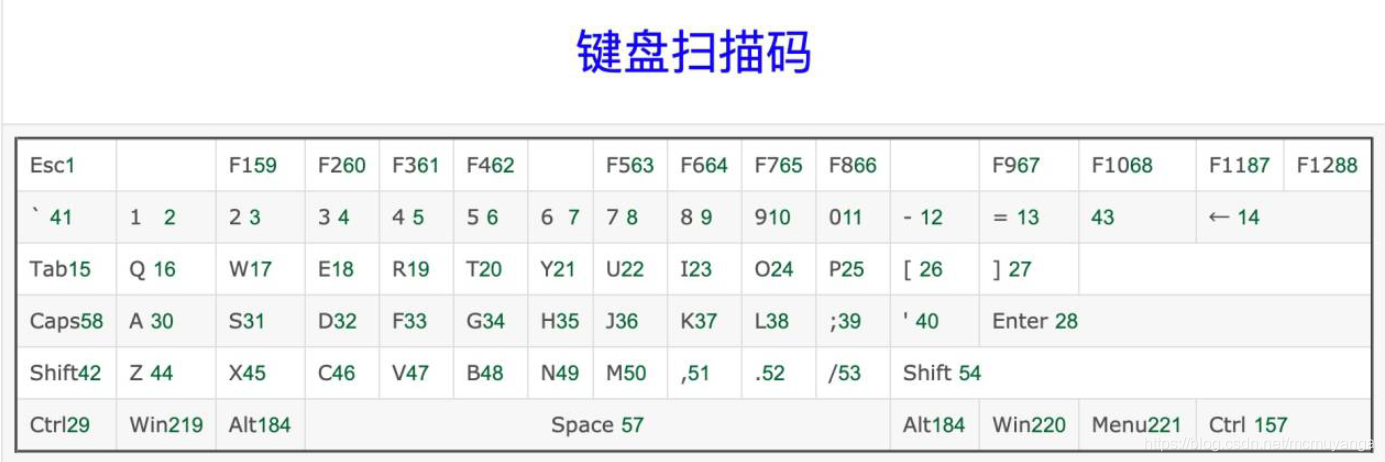
所以刚刚的上下左右对应的是IKJL

画出迷宫，走一下顺序是LKKKLLKLKKKLLLKKKLLLLLL

拿去md5加密一下

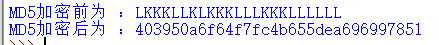
flag{403950a6f64f7fc4b655dea696997851}