LeetCode--004--寻找两个有序数组的中位数（java）

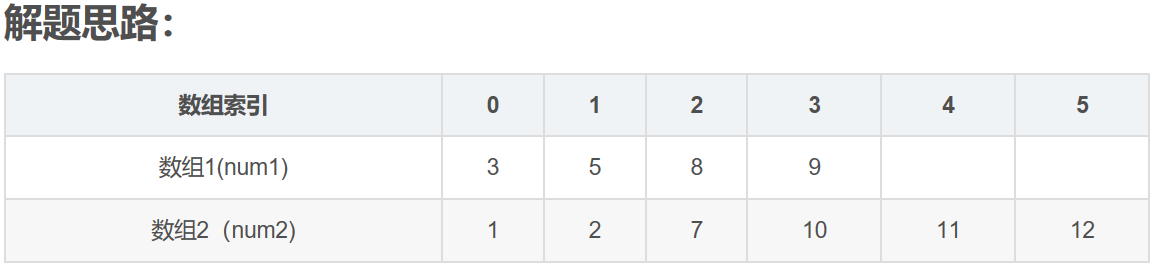
其中，N1=4,N2=6,size=4+6=10.

1，现在有的是两个已经排好序的数组，结果是要找出这两个数组中间的数值，如果两个数组的元素个数为偶数，则输出的是中间两个元素的平均值。
2，可以想象，如果将数组1随便切一刀(如在3和5之间切一刀），数组1将分成两份，数组1左别的元素的个数为1，右边的元素的个数为3。

由于数组1和数组2最终分成的左右两份的个数是确定的，都是所有元素的个数的一半（size/2=5)所以我们也可以知道，此时对数组2应该切的一刀的位置应该在10和11之间，数组2左边的个数为4，右边的个数为2.才能使两个数组左右两边的元素个数加起来的和（1+4=2+3）相等。
另外，我们记在数组1靠近这一刀的左别的元素为L1（3）,右边元素为R1（5）.同理，记在数组2靠近这一刀的左别的元素为L2（10）,右边元素为R2（11）.
如果这一刀的位置是正确的，则应该有的结果是
L1<=R2
L2<=R1
这样就能确保，左边的元素都小于右边的元素了。

3，所以，我们只需要直接找出在数组1切这一刀的正确位置就可以了。
为了减少查找次数，我们对短的数组进行二分查找。将在数组1切割的位置记为cut1，在数组2切割的位置记为cut2，cut2=(size/2)-cut1。
cut1，cut2分别表示的是数组1，数组2左边的元素的个数。
4，切这一刀的结果有三种
1）L1>R2  则cut1应该向左移，才能使数组1较多的数被分配到右边。
2）L2>R1 则cut1应该向右移，才能使数组1较多的数被分配到左边。
3）其他情况（L1<=R2  L2<=R1），cut1的位置是正确的，可以停止查找，输出结果。
5，其他说明
1）考虑到边界条件，就是cut的位置可能在边缘，就是cut1=0或者cut1=N1，cut2=0或者cut2=N2的这些情况，我们将min和max两个特殊值分别加在数组1和数组2的两端，就可以统一考虑了。还有N1个数为0的时候，直接输出结果即可。
2）为了减少查找时间，使用的是二分查找，就是cut1的位置是一半一半的查找的，实现时间只要log（N），不然就会超时。所以，我们不能只是简单地将cut1–或者cut1++，而是要记下每次cut1的区域范围，我们将cut1的范围记录下来，用[cutL,cutR]表示。一开始cut1的范围是[cutL,cutR]=[0，N1]，
如果L1>R2  则cut1应该向左移，才能使数组1较多的数被分配到右边。cut1的范围就变成了[cutL,cut1-1]，下次的cut1的位置就是cut1 = (cutR - cutL) / 2 + cutL;。
如果L2>R1 则cut1应该向右移，才能使数组1较多的数被分配到左边。cut1的范围就变成了[cut1+1,cutR]，下次的cut1的位置就是cut1 = (cutR - cutL) / 2 + cutL;。
3）数组的元素个数和是奇数的情况下，中间的元素应该就是min(R1,R2),只需另外处理输出就可以了。

time log(min(m,n))

space o(1)

 class Solution {
     public static double findMedianSortedArrays(int[] nums1, int[] nums2) {
         if(nums1.length > nums2.length){
             return findMedianSortedArrays(nums2, nums1);
         }
         int len = nums1.length + nums2.length;
         int cut1 = 0;
         int cut2 = 0;
         int cutL = 0;
         int cutR = nums1.length;
         while(cut1 <= nums1.length){
             cut1 = (cutR - cutL)/2 + cutL;
             cut2 = len/2 - cut1;
             double L1 = (cut1 == 0 )? Integer.MIN_VALUE:nums1[cut1 - 1];
             double L2 = (cut2 == 0 )? Integer.MIN_VALUE:nums2[cut2 - 1];
             double R1 = (cut1 == nums1.length )? Integer.MAX_VALUE:nums1[cut1];
             double R2 = (cut2 == nums2.length )? Integer.MAX_VALUE:nums2[cut2];
             if(L1>R2){
                 cutR = cut1 - 1;
             }else if(L2 > R1){
                 cutL = cut1 + 1;
             }else{
                 if(len %2 == 0){
                     L1 = (L1 > L2) ? L1 : L2;
                     R1 = (R1 > R2 )? R2 : R1;
                     return (L1+R1)/2;
                 }else{
                     R1 = (R1 < R2) ? R1 : R2;
                     return R1;
                 }
             }
         }
     return -1;
     }

 }

转自https://blog.csdn.net/chen_xinjia/article/details/69258706

2019-03-11 23:06:05