记录结果再利用的"动态规划"之背包问题

参考《挑战程序设计竞赛》p51

https://www.cnblogs.com/Ymir-TaoMee/p/9419377.html

01背包问题

• 问题描述：有n个重量和价值分别为w_i、v_i的物品，从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和的最大值。

input:

4
5

2 3

1 2

3 4

2 2

output:

7(选择第0、1、 3号物品）

朴素解法：

c++版：

#include <iostream>
using namespace std;

int n,W;
int *w,*v;//数组的指针

int max(int x, int y)
{
    if (x>y) return x;
    return y;
}

int rec(int i, int j)//从数组下标为i的物品开始往后挑选总重小于j的物体，i从0开始
{
    int res;
    if (i==n) res=0;//没有物品了
    else if (j<w[i]) res=rec(i+1,j);//重量j小于该组物品的重量，不能取
    else res=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]);//重量j大于该组物品的重量，能取；挑选和不挑选都尝试一下
    return res;
}

int main()
{
    cin >> n >> W;//n组物品，W:总重量
    w = new int[n];
    v = new int[n];
    for (int i=0; i<n; i++) cin >> w[i] >> v[i];
    cout << rec(0,W) << endl;
}

Java版本

package 记忆化搜索;

import java.util.Scanner;

public class Main {
	static int[] w, v;

	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int W=sc.nextInt();
		w = new int[n];
	    v = new int[n];
	    for (int i=0; i<n; i++) {
	    	w[i]=sc.nextInt();
	    	v[i]=sc.nextInt();
	    }
	    System.out.println(rec(0,W));
	}

	private static int rec(int i, int j) {
		if (i==w.length) {
			return 0;
		}
		if (j<w[i]) {
			return rec(i+1, j);
		}
		int a=rec(i+1, j);
		int b=rec(i+1, j-w[i])+v[i];
		return Math.max(a, b);
	}

}

---

这种方法的搜索深度是n，而且每一层的搜索都需要两次分支，最坏就需要O(2ⁿ)的时间。当n比较大时就没办法解了。所以要怎么办才好呢?为了优化之前的算法，我们看一下针对样例输人的情形下rec递归调用的情况。以下是rec(i,j)的模拟情况，i:第几组物品，j:重量

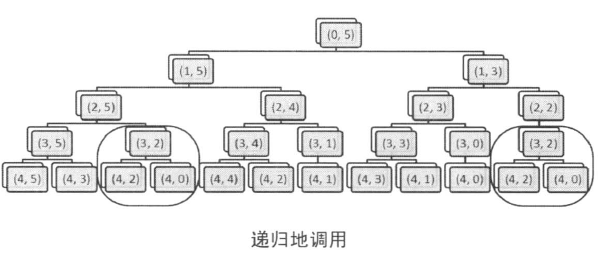
如图所示，rec以(3,2)为 参数调用了两次。如果参数相同，返回的结果也应该相同，于是第二次调用时已经知道了结果却白白浪费了计算时间。让我们在这里把第1次计算时的结果记录下来，省略掉第二次以后的重复计算试试看。

这微小的改进能降低多少复杂度呢?对于同样的参数，只会在第一次被调用到时执行递归部分，第二次之后都会直接返回。参数的组合不过nW种，而函数内只调用2次递归，所以只需要O(nW)的复杂度就能解决这个问题。只需略微改良，可解的问题的规模就可以大幅提高。这种方法一般被称为记忆化搜索。

c++版本：

#include <iostream>
#include <cstring>
using namespace std;

int n,W;
int *w,*v;
int **dp;

int max(int x, int y)
{
    if (x>y) return x;
    return y;
}

int rec(int i, int j)//从数组下标为i的物品开始往后挑选总重小于j的物体
{
    if (dp[i][j]>=0) return j[i[dp]];//和dp[i][j]的意义一样
    int res;
    if (i==n) res=0;
    else if (j<w[i]) res=rec(i+1,j);
    else res=max(rec(i+1,j),rec(i+1,j-w[i])+v[i]);
    dp[i][j] = res;
    return res;
}

int main()
{
    cin >> n >> W;
    w = new int[n];
    v = new int[n];
    dp = new int*[n+1];
    for (int i=0; i<=n; i++)
    {
        dp[i] = new int[W+1];
        memset(dp[i],-1,sizeof(int)*(W+1));
    }
    for (int i=0; i<n; i++) cin >> w[i] >> v[i];
    cout << rec(0,W) << endl;
}

　Java版本：

package 记忆化搜索;

import java.util.Arrays;
import java.util.Scanner;

public class Main {
	static int[] w, v;
	static int[][] dp;
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int W=sc.nextInt();
		w = new int[n];
	    v = new int[n];
	    for (int i=0; i<n; i++) {
	    	w[i]=sc.nextInt();
	    	v[i]=sc.nextInt();
	    }
	    dp=new int[n+1][W+1];
	    for (int i = 0; i < dp.length; i++) {
	    	Arrays.fill(dp[i], -1);
		}

	    System.out.println(rec(0,W));
	}

	private static int rec(int i, int j) {
		if (dp[i][j]>=0) {
			return dp[i][j];
		}
		if (i==w.length) {
			return 0;
		}
		if (j<w[i]) {
			return rec(i+1, j);
		}
		int a=rec(i+1, j);
		int b=rec(i+1, j-w[i])+v[i];
		int res=Math.max(a, b);
		dp[i][j]=res;
		return res;
	}

}

 接下来，我们来仔细研究一下前面的算法利用到的这个记忆化数组。记dp[i][j]为 根据rec的定义，从第i个物品开始挑选总重小于j时，总价值的最大值。于是我们有如下递推式 :

dp[i+1][j] := 从前i+1个物品(即从编号为0到i这i+1个物品)中选出总重量不超过j的物品时总价值的最大值
dp[0][j] = 0
                 /  dp[i][j]  (j<w[i]时)
dp[i+1][j] = 
                 \  max(dp[i][j],dp[i][j-w[i]]+v[i])  (其它情况下)

如上所示，不同写递归函数，直接利用递推式将各项的值计算出来，简单地用二重循环也可以解决这一问题，复杂度为O(nW)，与记忆化搜索是一样的，但是简洁了很多，这种方法叫做动态规划，即常说的DP：

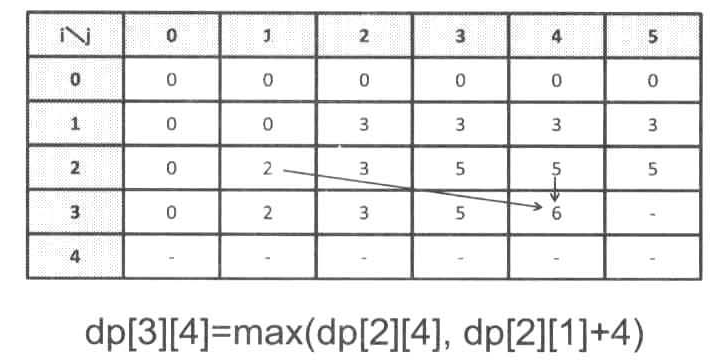
c++版本解法：

#include <iostream>
#include <cstring>
using namespace std;

int n,W;
int *w,*v;
int **dp;

int max(int x, int y)
{
    if (x>y) return x;
    return y;
}

int main()
{
    cin >> n >> W;
    w = new int[n];
    v = new int[n];
    dp = new int*[n+1];
    for (int i=0; i<=n; i++)
    {
        dp[i] = new int[W+1];
        memset(dp[i],0,sizeof(int)*(W+1));
    }
    for (int i=0; i<n; i++) cin >> w[i] >> v[i];
    for (int i=0; i<n; i++)
    {
        for (int j=0; j<=W; j++)
        {
            if (j<w[i]) dp[i+1][j]=dp[i][j];
            else dp[i+1][j] = max(dp[i][j],dp[i][j-w[i]]+v[i]);
        }
    }
    cout << dp[n][W] << endl;
}

java版本：

参考代码：https://www.acwing.com/problem/content/submission/code_detail/3617/

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {

        Scanner scanner=new Scanner(System.in);
        int n=scanner.nextInt();
        int m=scanner.nextInt();
        int v[]=new int[n+1];
        int w[]=new int[n+1];
        for (int i = 0; i <n; i++) {
            v[i]=scanner.nextInt();
            w[i]=scanner.nextInt();
        }
        int f[][]=new int[n+1][m+1];
        for (int i = 0; i <n ; i++) {
            for (int j = 0; j <=m ; j++) {
                 if(j<v[i])
                f[i+1][j]=f[i][j];
                else
                f[i+1][j]=Math.max(f[i][j],f[i][j-v[i]]+w[i]);
            }
        }

        System.out.println(f[n][m]);
    }
}　

---

完全背包问题

• 问题描述：有n种重量和价值分别为w_i，v_i的物品，从这些物品中挑选总重量不超过W的物品，求出挑选物品价值总和的最大值，在这里，每种物品可以挑选任意多件。

分析：这次同一种类的物品可以选择任意多件了，尝试着写出递推关系：
　　dp[i+1][j] := 从前i+1种(编号)物品中挑选总重量不超过j时总价值的最大值.
　　dp[0][j]=0
　　dp[i+1][j]=max{dp[i][j-k*w[i]]+k*v[i]|k≥0}

#include <iostream>
#include <cstring>
using namespace std;

int n,W;
int * w;
int * v;
int **dp;

int max(int x, int y)
{
    if (x>y) return x;
    return y;
}

int main()
{
    cin >> n >> W;
    w = new int[n];
    v = new int[n];
    for (int i=0; i<n; i++)
    {
        cin >> w[i] >>v[i];
    }
    dp = new int*[n+1];
    for (int i=0; i<=n; i++)
    {
        dp[i] = new int[W+1];
        memset(dp[i],0,sizeof(int)*(W+1));
    }
    for (int i=0; i<n; i++)
    {
        for (int j=0; j<=W; j++)
        {
            for (int k=0; k*w[i]<=j; k++)
            {
                dp[i+1][j] = max(dp[i+1][j],dp[i][j-k*w[i]]+k*v[i]);
            }
        }
    }
    cout << dp[n][W] << endl;
}

上面的程序是三重循环的，关于k的循环最坏可能从0到W，所以这个算法的复杂度为O(nW²),这样并不够好
我们来找一找这个算法中多余的计算(已经知道结果的计算)，在dp[i+1][j]的计算中选择k(k≥1)个的情况，与在dp[i+1][j-w[i]]的计算中选择k-1个情况是相同的，所以dp[i+1][j]的递推中k≥1部分的计算已经在dp[i+1][j-w[i]]的计算中完成了：
dp[i+1][j]
= max{dp[i][j-k*w[i]]+k*v[i]|k≥0}
= max(dp[i][j],max{dp[i][j-k*w[i]]+k*v[i]|k≥1})    //将k=0;k>=1的情况分开
= max(dp[i][j],max{dp[i][(j-w[i])-k*w[i]]+k*v[i]|k≥0}+v[i])//令k=k+1
= max(dp[i][j],dp[i+1][j-w[i]]+v[i])   //因为dp[i+1][j-w[i]]=dp[i][(j-w[i])-k*w[i]]+k*v[i]
即：dp[i+1][j] = max(dp[i][j],dp[i+1][j-w[i]]+v[i])
这样处理之后，就不需要关于k的循环了，现在的复杂度为O(nW):

#include <iostream>
#include <cstring>
using namespace std;

int n,W;
int * w;
int * v;
int **dp;

int max(int x, int y)
{
    if (x>y) return x;
    return y;
}

int main()
{
    cin >> n >> W;
    w = new int[n];
    v = new int[n];
    for (int i=0; i<n; i++)
    {
        cin >> w[i] >>v[i];
    }
    dp = new int*[n+1];
    for (int i=0; i<=n; i++)
    {
        dp[i] = new int[W+1];
        memset(dp[i],0,sizeof(int)*(W+1));
    }
    for (int i=0; i<n; i++)
    {
        for (int j=0; j<=W; j++)
        {
            if (j<w[i]) dp[i+1][j] = dp[i][j];
            else dp[i+1][j] = max(dp[i][j],dp[i+1][j-w[i]]+v[i]);
        }
    }
    cout << dp[n][W] << endl;
}　　

---

完全背包问题的变种

LeetCode .322

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:

输入: coins = [2], amount = 3
输出: -1

最长公共子序列问题

• 问题描述：给定两个字符串s₁s₂…s_n和t₁t₂…t_n。求这两个字符串最长的公共子序列的长度。

input:

n=4

m=4
s = "abcd"

t = "becd"

output:
3("bcd")

 

分析：这个问题是被称为最长公共子序列问题(LCS,Longest Common Subsequence)的著名问题。不妨使用下面的定义：
dp[i][j] :=s₁…s_i和t₁…t_j对应的LCS的长度
由此，s₁…s_i+1和t₁…t_j+1对应的公共子列可能是
①当s_i+1=t_j+1时，在s₁…s_i和t₁…t_j的LCS末尾追加上s_i+1；
②s₁…s_i和t₁…t_j+1的LCS；
③s₁…s_i+1和t₁…t_j和LCS；

三者中的某一个，所以就有如下的递推关系成立：
                      /  max(dp[i][j]+1,dp[i][j+1],dp[i+1][j])  (s_i+1=t_j+1)
dp[i+1][j+1] = 
                      \  max(dp[i][j+1],dp[i+1][j])  (其它情况下)
然而，稍微思考一下，就能发现当s_i+1=t_j+1时，只需令dp[i+1][j+1]=dp[i][j]+1就可以了
于是，总的递推式可写为：
                     /  dp[i][j]+1  (s_i+1=t_j+1)
dp[i+1][j+1] = 
                      \  max(dp[i][j+1],dp[i+1][j])  (其它情况下)
复杂度为O(nm)，dp[n][m]就是LCS的长度

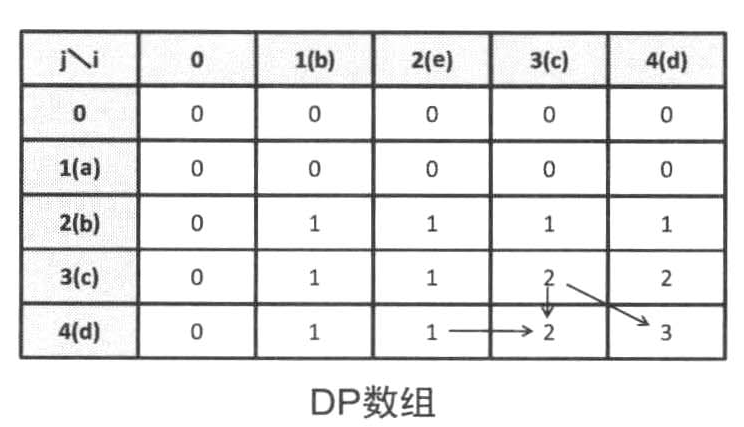
c++版本：

#include <iostream>
#include <cstring>
using namespace std;

int n,m;
char * s;
char * t;
int **dp;

int max(int x, int y)
{
    if (x>y) return x;
    return y;
}

int main()
{
    cin >> n >> m;
    s = new char[n+1];
    t = new char[m+1];
    for (int i=0; i<n; i++)
    {
        cin >> s[i];
    }
    for (int i=0; i<m; i++)
    {
        cin >> t[i];
    }
    dp = new int*[n+1];
    for (int i=0; i<=n; i++)
    {
        dp[i] = new int[m+1];
        memset(dp[i],0,sizeof(int)*(m+1));
    }
    for (int i=0; i<n; i++)
    {
        for (int j=0; j<m; j++)
        {
            if (s[i]==t[j]) dp[i+1][j+1]=dp[i][j]+1;
            else dp[i+1][j+1]=max(dp[i+1][j],dp[i][j+1]);
        }
    }
    cout << dp[n][m] << endl;
}

Java版本

package 记忆化搜索;

import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int m=sc.nextInt();
		String s=sc.next();
		String t=sc.next();
		int [][]dp=new int[n+1][m+1];
		for (int i=0; i<n; i++)
	    {
	        for (int j=0; j<m; j++)
	        {
	            if (s.charAt(i)==t.charAt(j)) dp[i+1][j+1]=dp[i][j]+1;
	            else dp[i+1][j+1]=Math.max(dp[i+1][j],dp[i][j+1]);
	        }
	    }
		System.out.println(dp[n][m]);
	}

}