HDU 2842 Chinese Rings(常数矩阵)

Chinese Rings

转载自:点这里

【题目链接】Chinese Rings

【题目类型】常数矩阵

&题意：

一种中国环，解开第k个环需要先解开全部的前(k-2)个环，并留有第(k-1)环。问解开n环最少需要几步。

&题解：

题目规定如果要拆第n个环，那么第n-1个要挂着，所有前n-2个环都要被拆下。那么我们设f(n)表示拆下前n个环的最少的步骤.

那么考虑第n个环的情况，第n-1个环必须要挂着，n-2环要拆下，那么这一步就要f(n-2)，拆下第n个需要1步。然后只剩下第n-1个环，由于n-1环需要第n-2环挂着，所以我们需要把前n-2个环挂上去，所以需要f(n-2)，剩下n-1个需要拆下需要f(n-1)。那么总的需要f(n) = f(n-2)+1+f(n-2)+f(n-1)

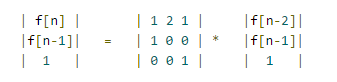
&代码：

#include <cstdio>
#include <iostream>
#include <set>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <queue>
#include <vector>
using namespace std;
#define INF 0x3f3f3f3f
using ll=long long;
const int maxn= 1e3 +9;
ll n,M=200907;
typedef vector<ll>vec;
typedef vector<vec> mat;
mat mul(mat &A,mat &B)
{
	mat C(A.size(),vec(B.size()));
	for(int i=0;i<A.size();i++)
	for(int k=0;k<B.size();k++)
	for(int j=0;j<B[0].size();j++){
		C[i][j]=(C[i][j]+A[i][k]*B[k][j])%M;
	}
	return C;
}
mat bin_pow(mat A,ll n)
{
	mat B(A.size(),vec(A.size()));
	for(int i=0;i<A.size();i++){
		B[i][i]=1;
	}
	while(n>0){
		if(n&1)
			B=mul(B,A);
		A=mul(A,A);
		n>>=1;
	}
	return B;
}
mat A(3,vec(3));
void Init()
{
	for(int i=0;i<3;i++)
	for(int j=0;j<3;j++)
		A[i][j]=0;
	int c=1;
	int t[]={1,2,c};
	for(int i=0;i<3;i++)
		A[0][i]=t[i];
	A[1][0]=A[2][2]=1;
}
int main()
{
//	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	freopen("E:1.txt","r",stdin);
	while(cin>>n){
		if(n==0)break;
		Init();
		if(n<=2) cout<<n<<endl;
		else{
			A=bin_pow(A,n-2);
			int t[]={2,1,1};
			ll ans=0;
			for(int i=0;i<3;i++)
				ans=(ans+A[0][i]*t[i])%M;
			cout<<ans<<endl;
		}
	}
	return 0;
}