51nod 1624 取余最长路

http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1624

题意：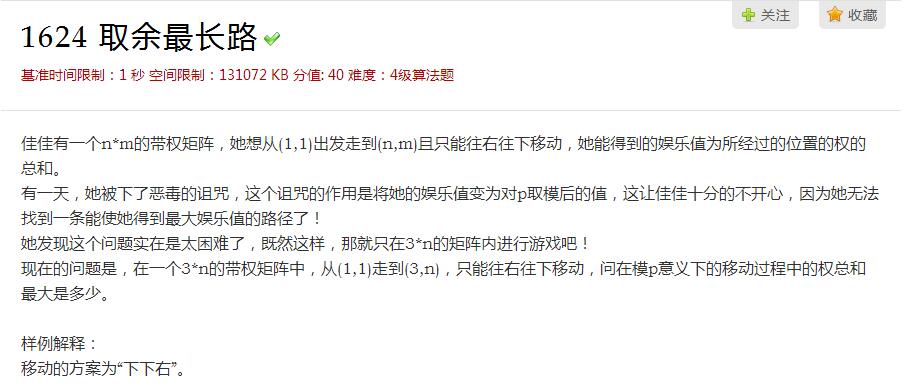

思路：
因为一共只有3行，所以只需要确定第一行和第二行的转折点就行，如果是暴力枚举的话，时间复杂度会比较高，为了降低时间复杂度，可以采用枚举第一行，然后二分第二行的方法来做。

设sum(i,l,r)表示第i行从l到r元素的和，则答案可以表示为sum(1,1,x)+sum(2,x,y)+sum(3,y,n)%p。

前缀和一下转化成(S3[n]-S3[y-1])+S2[y]+(S1[x]-S2[x-1])%p，从小到大枚举y，将所有(S1[x]-S2[x-1])扔到一个集合里，用个set就能轻松实现了。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn = +;

 int n, p;
 ll sum[][maxn];

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d",&n,&p))
     {
         sum[][]=sum[][]=sum[][]=;
         for(int i=;i<=;i++)
         {
             for(int j=;j<=n;j++)
             {
                 int x; scanf("%d",&x);
                 sum[i][j]=(sum[i][j-]+x)%p;
             }
         }
         set<int> s;
         ll ans = ;
         for(int i=;i<=n;i++)
         {
             ll tmp = (sum[][i]-sum[][i-]+p)%p;
             s.insert(tmp);
             tmp=(sum[][i]-sum[][i-]+sum[][n]+p)%p;
             set<int>::iterator it = s.lower_bound(p-tmp);
             if(it!=s.begin())
                 ans=max(ans,tmp+*(--it));
         }
         printf("%lld\n",ans);
     }
     return ;
 }