（原）CNN中的卷积、1x1卷积及在pytorch中的验证

转载请注明处处：

http://www.cnblogs.com/darkknightzh/p/9017854.html

参考网址：

https://pytorch.org/docs/stable/nn.html?highlight=conv2d#torch.nn.Conv2d

https://www.cnblogs.com/chuantingSDU/p/8120065.html

https://blog.csdn.net/chaolei3/article/details/79374563

1x1卷积

https://blog.csdn.net/u014114990/article/details/50767786

https://www.quora.com/How-are-1x1-convolutions-used-for-dimensionality-reduction

https://www.reddit.com/r/MachineLearning/comments/3oln72/1x1_convolutions_why_use_them/?st=is9xc9jn&sh=7b774d4d

理解错误的地方敬请谅解。

1.  卷积

才发现一直理解错了CNN中的卷积操作。

假设输入输出大小不变，输入是N*Cin*H*W，输出是N*Co*H*W。其中N为batchsize。卷积核的大小是k*k。实际上共有Cin*Co个k*k的卷积核，总共的参数是Cin*k*k*Co（无bias）或者Cin*k*k*Co+Co（有bias）。

pytorch中给出了conv2d的计算公式

（https://pytorch.org/docs/stable/nn.html?highlight=conv2d#torch.nn.Conv2d）：

$out({{N}_{i}},C{{o}_{j}})=bias(C{{o}_{j}})+\sum\limits_{k=0}^{Cin-1}{weight(C{{o}_{j}},k)*input({{N}_{i}},k)}$

其中weight即为卷积核，上式中输出的batch中的第N_i个特征图的第Co_j个特征，即为输入的第N_i个特征图的第k个特征，和第Co_j个卷积核中的第k个核进行卷积（cross-correlation）。

如下图所示，对于某个输入特征图，其某局域分别于Co个卷积核进行卷积，得到对应的特征Co_i，而后将这些特征拼接起来，得到最终的特征图。实际上每个卷积核都是k*k*Cin的大小。

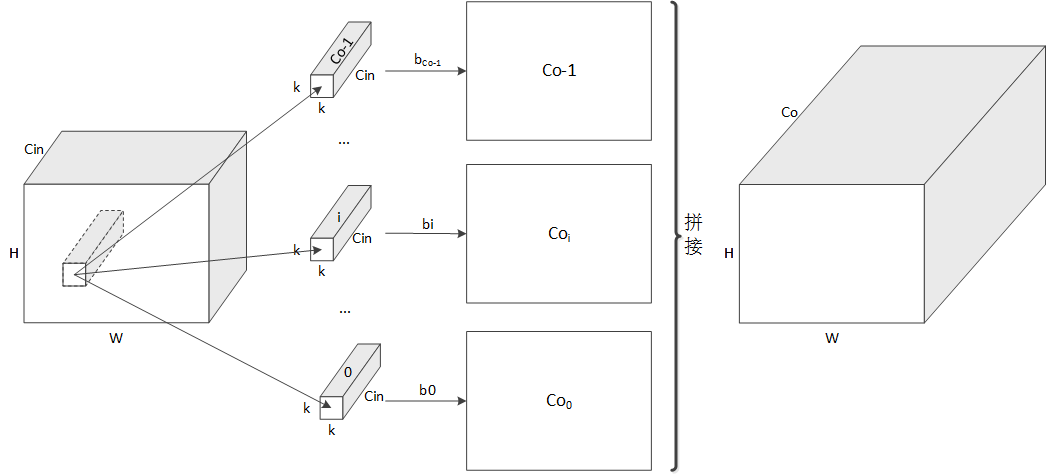
经过上面的卷积，就可以将输入的不同的通道的信息融合了（权重不同，类似于加权融合）。

如果输出Co数量大于输入Cin数量，输出特征数量就多于输入特征。否则输出就少于输入特征数量。

2.  1*1卷积

上面的卷积理解了，1*1卷积就好理解了。

1*1主要用于降维或者升维（看Cin和Co哪个更大），其核大小为1*1。

实际上卷积核的数量为Cin*1*1*Co=Cin*Co（无bias）或者Cin*Co+Co（有bias）。

计算时，通道方向上每个卷积核将输入按照通道进行加权，得到对应的输出特征，之后将这些特征拼接起来，即可得到最终的特征图。

3.  pytorch中的验证

代码：

 from __future__ import print_function
 from __future__ import division

 import torch.nn as nn
 import numpy as np

 class testNet(nn.Module):
     def __init__(self):
         super(testNet, self).__init__()
         self.conv1 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=5, stride=1, padding=1, bias=True)

     def forward(self, x):
         x = self.conv1(x)
         return x

 def get_total_params(model):
     model_parameters = filter(lambda p: p.requires_grad, model.parameters())
     num_params = sum([np.prod(p.size()) for p in model_parameters])
     return num_params

 def main():
     net = testNet()
     print(get_total_params(net))

 if __name__ == '__main__':
     main()

上面代码中get_total_params用于得到模型总共的参数。

当kernel_size=5，bias=True时，参数共计760个：3*5*5*10+10=760。

当kernel_size=5，bias=False时，参数共计750个：3*5*5*10=750。

当kernel_size=1，bias=True时，参数共计40个：3*1*1*10+10=40。

当kernel_size=1，bias=False时，参数共计30个：3*1*1*10=30。