常用七种排序的python实现

1 算法复杂度

算法复杂度分为时间复杂度和空间复杂度。其中，时间复杂度是指执行算法所需要的计算工作量；而空间复杂度是指执行这个算法所需要的内存空间。

算法的复杂性体现在运行该算法时的计算机所需资源的多少上，计算机资源最重要的是时间和空间资源，因此复杂度分为时间和空间复杂度。用大O表示。

常见的时间复杂度（按效率排序）

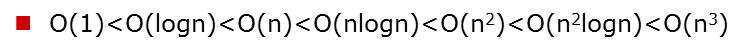
2 冒泡排序

冒泡法：第一趟：相邻的两数相比，大的往下沉。最后一个元素是最大的。

第二趟：相邻的两数相比，大的往下沉。最后一个元素不用比。

 def bubble_sort(array):

     for i in range(len(array)-1):

         for j in range(len(array) - i -1):

             if array[j] > array[j+1]:

                 array[j], array[j+1] = array[j+1], array[j]

时间复杂度：O(n^2)

稳定性：稳定

改进：如果一趟比较没有发生位置变换，则认为排序完成

 def bubble_sort(array):

     for i in range(len(array)-1):

         current_status = False

         for j in range(len(array) - i -1):

             if array[j] > array[j+1]:

                 array[j], array[j+1] = array[j+1], array[j]

                 current_status = True

         if not current_status:

             break

3 直接选择排序

选择排序法：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放到序列的起始位置，直到全部排完。

 def select_sort(array):

     for i in range(len(array)-1):

         min = i

         for j in range(i+1, len(array)):

             if array[j] < array[min]:

                 min = j

         array[i], array[min] = array[min], array[i]

时间复杂度：O(n^2)

稳定性：不稳定

4 直接插入排序

列表被分为有序区和无序区两个部分。最初有序区只有一个元素。
每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。
其实就相当于摸牌：

 def insert_sort(array):

     # 循环的是第二个到最后（待摸的牌）

     for i in range(1, len(array)):

         # 待插入的数（摸上来的牌）

         min = array[i]

         # 已排好序的最右边一个元素（手里的牌的最右边）

         j = i - 1

         # 一只和排好的牌比较，排好的牌的牌的索引必须大于等于0

         # 比较过程中，如果手里的比摸上来的大，

         while j >= 0 and array[j] > min:

             # 那么手里的牌往右边移动一位，就是把j付给j+1

             array[j+1] = array[j]

             # 换完以后在和下一张比较

             j -= 1

         # 找到了手里的牌比摸上来的牌小或等于的时候，就把摸上来的放到它右边

         array[j+1] = min

时间复杂度：O(n^2)

稳定性：稳定

5 快速排序

取一个元素p（通常是第一个元素，但是这是比较糟糕的选择），使元素p归位（把p右边比p小的元素都放在它左边，在把空缺位置的左边比p大的元素放在p右边）；
列表被p分成两部分，左边都比p小，右边都比p大；
递归完成排序。

 def quick_sort(array, left, right):

     if left < right:

         mid = partition(array, left, right)

         quick_sort(array, left,  mid-1)

         quick_sort(array, mid+1, right)

 def partition(array, left, right):

     tmp = array[left]

     while left < right:

         while left < right and array[right] >= tmp:

             right -= 1

         array[left] = array[right]

         while left < right and array[left] <= tmp:

             left += 1

         array[right] = array[left]

     array[left] = tmp

     return left

时间复杂度：O(nlogn)，一般情况是O(nlogn)，最坏情况（逆序）：O（n^2）

稳定性：不稳定

特点：就是快

6 堆排序

步骤：
　　建立堆
　　得到堆顶元素，为最大元素
　　去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
　　堆顶元素为第二大元素。
　　重复步骤3，直到堆变空。

 def sift(array, left, right):

     """调整"""

     i = left      # 当前调整的小堆的父节点

     j = 2*i + 1   # i的左孩子

     tmp = array[i]     # 当前调整的堆的根节点

     while j <= right:    # 如果孩子还在堆的边界内

         if j < right and array[j] < array[j+1]:   # 如果i有右孩子,且右孩子比左孩子大

             j = j + 1                              # 大孩子就是右孩子

         if tmp < array[j]:                         # 比较根节点和大孩子，如果根节点比大孩子小

             array[i] = array[j]                     # 大孩子上位

             i = j                                   # 新调整的小堆的父节点

             j = 2*i + 1                             # 新调整的小堆中I的左孩子

         else:                                       # 否则就是父节点比大孩子大，则终止循环

             break

     array[i] = tmp                                  # 最后i的位置由于是之前大孩子上位了，是空的，而这个位置是根节点的正确位置。

 def heap(array):

     n = len(array)

     # 建堆，从最后一个有孩子的父亲开始，直到根节点

     for i in range(n//2 - 1, -1, -1):

         # 每次调整i到结尾

         sift(array, i, n-1)

     # 挨个出数

     for i in range(n-1, -1, -1):

         # 把根节点和调整的堆的最后一个元素交换

         array[0], array[i] = array[i], array[0]

         # 再调整，从0到i-1

         sift(array, 0, i-1)

时间复杂度：O(nlogn)，

稳定性：不稳定

特点：通常都比快排慢

7 为什么堆排比快排慢？


回顾一下堆排的过程：

1. 建立最大堆（堆顶的元素大于其两个儿子，两个儿子又分别大于它们各自下属的两个儿子... 以此类推）
2. 将堆顶的元素和最后一个元素对调（相当于将堆顶元素（最大值）拿走，然后将堆底的那个元素补上它的空缺），然后让那最后一个元素从顶上往下滑到恰当的位置（重新使堆最大化）。
3. 重复第2步。

　　这里的关键问题就在于第2步，堆底的元素肯定很小，将它拿到堆顶和原本属于最大元素的两个子节点比较，它比它们大的可能性是微乎其微的。实际上它肯定小于其中的一个儿子。而大于另一个儿子的可能性非常小。于是，这一次比较的结果就是概率不均等的，根据前面的分析，概率不均等的比较是不明智的，因为它并不能保证在糟糕情况下也能将问题的可能性削减到原本的1/2。可以想像一种极端情况，如果a肯定小于b，那么比较a和b就会什么信息也得不到——原本剩下多少可能性还是剩下多少可能性。
　　在堆排里面有大量这种近乎无效的比较，因为被拿到堆顶的那个元素几乎肯定是很小的，而靠近堆顶的元素又几乎肯定是很大的，将一个很小的数和一个很大的数比较，结果几乎肯定是“小于”的，这就意味着问题的可能性只被排除掉了很小一部分。
　　这就是为什么堆排比较慢（堆排虽然和快排一样复杂度都是O(NlogN)但堆排复杂度的常系数更大）。
MacKay也提供了一个修改版的堆排：每次不是将堆底的元素拿到上面去，而是直接比较堆顶（最大）元素的两个儿子，即选出次大的元素。由于这两个儿子之间的大小关系是很不确定的，两者都很大，说不好哪个更大哪个更小，所以这次比较的两个结果就是概率均等的了

8 归并排序

思路：

一次归并：将现有的列表分为左右两段，将两段里的元素逐一比较，小的就放入新的列表中。比较结束后，新的列表就是排好序的。

然后递归。

 # 一次归并

 def merge(array, low, mid, high):

     """

     两段需要归并的序列从左往右遍历，逐一比较，小的就放到

     tmp里去，再取，再比，再放。

     """

     tmp = []

     i = low

     j = mid +1

     while i <= mid and j <= high:

         if array[i] <= array[j]:

             tmp.append(array[i])

             i += 1

         else:

             tmp.append(array[j])

             j += 1

     while i <= mid:

         tmp.append(array[i])

         i += 1

     while j <= high:

         tmp.append(array[j])

         j += 1

     array[low:high+1] = tmp

 def merge_sort(array, low, high):

     if low < high:

         mid = (low + high) // 2

         merge_sort(array, low, mid)

         merge_sort(array, mid+1, high)

         merge(array, low, mid, high)

时间复杂度：O(nlogn)

稳定性：稳定

快排、堆排和归并的小结

三种排序算法的时间复杂度都是O(nlogn)

一般情况下，就运行时间而言：
　　　　快速排序 < 归并排序 < 堆排序

三种排序算法的缺点：
　　快速排序：极端情况下排序效率低
　　归并排序：需要额外的内存开销
　　堆排序：在快的排序算法中相对较慢

9 希尔排序

希尔排序是一种分组插入排序算法。
首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；
取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。

 def shell_sort(li):

     """希尔排序"""

     gap = len(li) // 2

     while gap > 0:

         for i in range(gap, len(li)):

             tmp = li[i]

             j = i - gap

             while j >= 0 and tmp < li[j]:

                 li[j + gap] = li[j]

                 j -= gap

             li[j + gap] = tmp

         gap //= 2

时间复杂度:O((1+τ)n)

不是很快，位置尴尬

10 排序小结