2017普及组D1T3 洛谷P3956 棋盘

题目描述

有一个m×m的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的），你只能向上、下、左、右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费1个金币。

另外，你可以花费 2个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用，而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法；只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入输出格式

输入格式：

第一行包含两个正整数m，n，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的nn行，每行三个正整数x, y, c，分别表示坐标为(x,y)的格子有颜色c。

其中c=1代表黄色，c=0 代表红色。相邻两个数之间用一个空格隔开。棋盘左上角的坐标为(1, 1)，右下角的坐标为(m, m)。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是(1, 1)一定是有颜色的。

输出格式：

一个整数，表示花费的金币的最小值，如果无法到达，输出-1−1。

输入输出样例

输入样例#1：

输出样例#1：

输入样例#2：

输出样例#2：

-1

说明

输入输出样例 1 说明

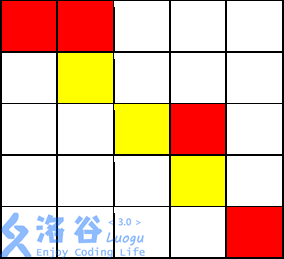
从(1,1)开始，走到(1,2)不花费金币

从(1,2)向下走到(2,2)花费1枚金币

从(2,2)施展魔法，将(2,3)变为黄色，花费2枚金币

从(2,2)走到(2,3)不花费金币

从(2,3)走到(3,3)不花费金币

从(3,3)走到(3,4)花费1枚金币

从(3,4)走到(4,4)花费1枚金币

从(4,4)施展魔法，将(4,5)变为黄色，花费2枚金币，

从(4,4)走到(4,5)不花费金币

从(4,5)走到(5,5)花费1枚金币

共花费8枚金币。

输入输出样例 2 说明

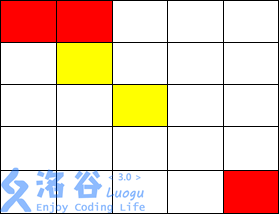
从(1,1)走到(1,2),不花费金币

从(1,2)走到(2,2),花费1金币

施展魔法将(2,3)变为黄色,

并从(2,2)走到(2,3)花费2金币

从(2,3)走到(3,3)不花费金币

从(3,3)只能施展魔法到达(3,2),(2,3),(3,4),(4,3)

而从以上四点均无法到达(5,5),故无法到达终点,输出−1

数据规模与约定

对于 30%的数据, 1 ≤ m ≤ 5, 1 ≤ n ≤ 101≤m≤5,1≤n≤10。

对于 60%的数据, 1 ≤ m ≤ 20, 1 ≤ n ≤ 2001≤m≤20,1≤n≤200。

对于 100%的数据, 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,0001≤m≤100,1≤n≤1,000。

下面就是我的方法咯！

（未完待续。。。）