NOIP的模板--考前复习

距离NOIP还有-1天

可以去放弃一些巨难得题目去搞一些模板了

　　　　　　　　　　　　　　-------在校老师的原话

一·快排

虽然可以手打，最好用STL，里面有很多优化，会快很多

 #include<iostream>
 #include<algorithm>
 using namespace std;
 struct node
 {
     int x,y;
 }a[maxn];
 bool cmp(node a,node b)
 {
     return a.x<b.x;
 }
 int main()
 {
     sort(a+,a++n,cmp);
     return ;
  } 

二·冰茶姬

一个很好用，很好压行的神奇初级（虽然难题是真的不会）黑科技。

  int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}

三·快速幂||取模运算（就是快速幂里要取模）

 int KSM(int a,int b,int c)
 {
     int ans=;a%=c;
     while(b>)
     {
         if(b%==)ans=ans*a%c;
         b/=;a=a*a%c;
     }
     return ans;
 }

四·线性筛素数

这题有很多方法，比如瞎搞，因为大于10的素数一定都在6的倍数的两边，至于证明什么的可以去找数竞。

或者可以用埃筛（几乎是线性），或者用欧筛

• 以6的倍数来搞事的判断方法：

•  bool prime(int n)
   {
       if(n==)return false;
       if(n==||n==)return true;
       if(n%!=&&n%!=)return false;
       for(int i=;i*i<=n;i+=)
       if(n%i==||n%(i+)==)retrun false;
       return true;
   }

  埃筛

•  void make_prime()
   {
       memset(prime,true,sizeof(prime));
       prime[]=prime[]=false;
       int t=sqrt(MAXN);
       for(register int i=;i<=t;i++)if(prime[i])
       for(register int j=*i;j<MAXN,j+=i)
       prime[j]=false;
   }

  欧筛

•  void make_prime()
   {
       memset(prime,true,sizeof(prime));
       prime[] = prime[] = false;
       for( int i = ; i <= MAXN; i++) {
           if( prime[i] ) Prime[ num ++ ] = i;
           for(int j = ;j<num && i*Prime[j] < MAXN; j++) {
               prime[ i*Prime[j] ] = false;
               if( !( i%Prime[j] ) ) break;
           }
       }
       return;
   }

  还有一些其他搞事的办法，但埃筛，一般就够用了

五·最小生成树

人生信条能打kruskal永远不打prim!!!!!!

 void kruskal()
 {
     int f1,f2,k,i;
     k=;
     for(i=;i<=n;i++)
     prt[i]=i;
     for(i=;i<=m;i++)
     {
         f1=find(a[i].x);
         f2=find(a[i].y);
         if(f1!=f2)
         {
             ans=ans+a[i].z;
             prt[f1]=f2;
             k++;
             if(k==n-)
             break;
         }
     }
     if(k<n-)
     {
         cout<<"orz"<<endl;
         bj=;
         return ;
     }
 }

六·单源最短路弱化版（SPFA）

能打SPFA不打dijkstra!!!!!!!!

 inline void spfa(int k)
 {
     queue< int >q;
     dis[k] = ; q.push(k); vis[k] = ;
     while(!q.empty()) {
         x = q.front(); q.pop(); vis[x] = ;
         for(int i = head[x]; i != ; i = way[i].next ) {
             if(dis[x] + way[i].w < dis[way[i].to]) {
                 dis[way[i].to] = dis[x] + way[i].w;
                 if(vis[way[i].to] == ) {
                     q.push(way[i].to);
                     vis[way[i].to] = ;
                 }
             }
         }
     }
 }

七·树状数组

 int lowbit(int x)
 {
     return x&(-x);
 }
 int add(int x,int y)
 {
     while(x<=n)
     {
         c[x]+=y;
         x+=lowbit(x);
     }
 }
 int sum(int x)
 {
     int res=;
     while(x>)
     {
         res+=c[x];
         x-=lowbit(x);
     }
     return res;
 }

八·乘法逆元

线性的，还有什么费马小，感觉没什么用，就没打

 int CFNY(int n)
 {
     inv[]=;
     cout<<<<endl;
     for(int i=;i<=n;i++)
     {
         inv[i]=(long long )(p-p/i)*inv[p%i]%p;
         cout<<inv[i]<<endl;
     }
 }

九·康托展开

绝对没人会在NOIP考这个东西，要是他考了，以后就可以说 这很NOIP。。。。

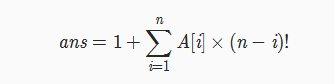
 ll kangtuo(ll x[])
 {
     ll p=;
     for(ll i=;i<=n;i++)
     {
         ll t=;
         for(ll j=i+;j<=n;j++)
         {
             if(x[i]>x[j])
             {
                 t++;
             }
         }
         p+=t*fc[n-i];
     }
     return p+;
 }

十·最近公共祖先（LCA）

 void dfs(int x,int father)//x为当前节点，father为其父节点
 {
     deep[x]=deep[father]+;//当前点的深度为其父节点深度加1
     parents[x][]=father;//当前点的2^0祖先(也就是上1级祖先)就是其父节点
     for(int i=;(<<i)<=deep[x];i++)
     {
         parents[x][i]=parents[parents[x][i-]][i-];
         //这里应该是整个预处理阶段中最有灵魂的部分了
         //x的2^i级祖先就是x的2^(i-1)级祖先的2^(i-1)级的祖先 。
         //2^i==2^(i-1)+2^(i-1),这个式子好像没什么可说的
     }
     for(int i=head[x];i;i=way[i].next)
     {
         int to=way[i].to;
         if(to!=father)
         dfs(to,x);
      }
  } 

 int lca(int a,int b)//a,b为两个要查询的点
 {
     if(deep[a]>deep[b])//我时刻保证a的深度比b的小
     {
         swap(a,b); //如果反了就换一下
     }
     for(int i=;i>=;i--)
     {
          if(deep[a]<=deep[b]-(<<i))
          b=parents[b][i];//将a和b跳的同一高度
     }
     if(a==b)//如果b在跳上来时和a一样了，那说明a就是a和b的LCA，直接返回就行了
     return a;
     for(int i=;i>=;i--)
     {
         if(parents[a][i]==parents[b][i])
         continue;
         else
         {
             a=parents[a][i];
             b=parents[b][i];//将a和b一起往上跳
         }
     }
     return parents[a][];//找出最后的答案
 }

十一·卢卡斯

只存在于组合数里的东西

 long long CC(long long n,long long m){
     if(m>n)
     return ;
     return ((c[n]*KSM(c[m],p-,p))%p*KSM(c[n-m],p-,p)%p);
 }
 long long  Lucas(long long n,long long m){
     if(!m)
     return ;
     return CC(n%p,m%p)*Lucas(n/p,m/p)%p;
 }

十二·二分图匹配

 int dfs(int t)
 {
     for (int i=; i<=n2; ++i)
         if (a[t][i] ==  && check[i] == )
         {
             check[i] = ;
             if (p[i] ==  || dfs(p[i]) == )
             {
                 p[i] = t;
                 return ;
             }
         }
     return ;
 }

十三·强连通分量（tarjan）

 void tarjan(int s)
 {
     dfn[s]=low[s]=++tim;
     in[s]=,stack[++top]=s;
     for(int i=head[s];i;i=edge[i].next)
     {
         int v=edge[i].to;
         if(!dfn[v])
         {
             tarjan(v);
             low[s]=min(low[v],low[s]);
         }
         else if(in[v]&&low[s]>dfn[v])low[s]=dfn[v];
     }
     if(dfn[s]==low[s])
     {
         int p;
         belong[s]=++cnt;
         do
         {
             p=stack[top--];
             in[p]=;
             belong[p]=cnt;
         }while(p!=s);
     }
 }

十四·割点（还是那个有名的tarjan）

 int tarjan(int x,int y)
 {
     low[x]=dfn[x]=++tim;
     int child=;
     for(int i=head[x];i;i=way[i].next)
     {
         int v=way[i].to ;
         if(!dfn[v])
         {
             tarjan(v,y);
             low[x]=min(low[x],low[v]);
             if(dfn[x]<=low[v]&&x!=y)
             {
                 cut[x]=;
             }
             if(x==y)
             {
                 child++;
             }
         }
         low[x]=min(low[x],dfn[v]);
         if(child>=&&x==y)
         {
             cut[x]=;
         }
     }
 }

十五·对拍之造数据（maker）Windows下

eg. 2个正整数x0​,y0​

 #include<bits/stdc++.h>
 using namespace std;
 int main()
 {
     freopen("data.in","w",stdout);
     srand(time(NULL));
     int n=rand();
     int m=rand();//可以在这里加模数来控制范围
     cout<<n<<" "<<m<<endl;
 }

十六·对拍之检查（check）Windows下

这个在用之前一定要先把所有的程序先跑一下，然后一定要在同一各根目录下，不然有可能会用一些很神奇的东西把源程序给覆盖掉

 #include<bits/stdc++.h>
 using namespace std;
 int main()
 {
     while()
     {
         system("maker");
         system("true");
         system("false");
         if(system("fc false.out true.out")
         {
             cout<<"WA"<<endl;
             break;
         }
         cout<<"AC"<<endl;
     }
     return ;
  } 

十七·缩点（还是那个tarjan）

 void tarjan(int x)
 {
     low[x]=dfn[x]=++tim;
     stac[++top]=x;
     vis[x]=;
     for(int i=head[x];i;i=edge[i].next)
     {
         int v=edge[i].to;
         if(!dfn[v])
         {
             tarjan(v);
             low[x]=min(low[x],low[v]);
         }
         else if(vis[v])
         {
             low[x]=min(low[x],dfn[v]);
         }
     }
     if(dfn[x]==low[x])
     {
         int y;
         while(y=stac[top--])
         {
             sd[y]=x;
             vis[y]=;
             if(x==y)
             break;
             p[x]+=p[y];
         }
     }
 }

十八·网络最大流（很NOIP的一个东西）

 int bfs()
 {
     memset(deep,0x3f,sizeof(deep));
     memset(in,,sizeof(in));
     deep[s]=;
     queue<int >q;
     q.push(s);
     while(!q.empty())
     {
         int x=q.front();
         q.pop();
         in[x]=;
         for(int i=head[x];i;i=way[i].next)
         {
             int v=way[i].to;
             if(deep[v]>deep[x]+&&way[i].value)
             {
                 deep[v]=deep[x]+;
                 if(in[v]==)
                 {
                     q.push(v);
                     in[v]=;
                 }
             }
         }
     }
     if(deep[t]!=0x3f3f3f3f)
     return ;
     return ;
 }
 int dfs(int x,int y)
 {
     ans=;
     if(x==t)
     return y;
     for(int i=head[x];i;i=way[i].next)
     {
         int v=way[i].to;
         if(way[i].value&&deep[v]==deep[x]+)
         {
             if(ans=dfs(v,min(y,way[i].value)))
             {
                 way[i].value-=ans;
                 way[i^].value+=ans;
                 return ans;
             }
         }
     }
     return ;
 }
 int dinic()
 {
     low=;
     while(bfs())
     {
         while(low=dfs(s,inf))
         maxnn+=low;
     }
     return maxnn;
 }

十九·最小费用最大流

 int spfa()
 {
     memset(dis,0x3f,sizeof(dis));
     memset(pre,,sizeof(pre));
     memset(in,,sizeof(in));
     queue<int >q;
     q.push(s);
     in[s]=;
     dis[s]=;
     while(!q.empty())
     {
         int x=q.front();
         q.pop();
         in[x]=;
         for(int i=head[x];i;i=way[i].next)
         {
             int v=way[i].to;
             int w=way[i].cost;
             if(way[i].value>&&dis[v]>dis[x]+w)
             {
                 dis[v]=dis[x]+w;
                 pre[v].from=x;
                 pre[v].edge=i;
                 if(in[v]==)
                 {
                     q.push(v);
                     in[v]=;
                 }
             }
         }
     }
     return dis[t]!=0x3f3f3f3f;
 }
 int ek()
 {
     ans=;
     cost=;
     int mi;
     int i;
     while(spfa())
     {
         mi=inf;
         for(i=t;i!=s;i=pre[i].from)
         {
             mi=min(mi,way[pre[i].edge].value);
         }
         for(i=t;i!=s;i=pre[i].from)
         {
             way[pre[i].edge].value-=mi;
             way[pre[i].edge^].value+=mi;
         }
         ans+=mi;
         cost+=mi*dis[t];
     }
     return ans;
 }

二十·高精度加减乘除模

 #include <bits/stdc++.h>
 using namespace std;
 struct Big
 {
     static const int BASE = ;
     static const int WIDTH = ;
     vector<long long> s;
     Big()
     {
         *this = ;
     }
     Big(const int &num)
     {
         *this = num;
     }

     Big operator=(int num)
     {
         s.clear();
         do
         {
             s.push_back(num % BASE);
             num /= BASE;
         } while (num > );
         return *this;
     }
     Big operator=(const string &str)
     {
         s.clear();
         int x, len = (str.length() - ) / WIDTH + ;
         for (int i = ; i < len; i++)
         {
             int end = str.length() - i * WIDTH;
             int start = max(, end - WIDTH);
             sscanf(str.substr(start, end - start).c_str(), "%lld", &x);
             s.push_back(x);
         }
         return *this;
     }
     bool operator<(const Big &b)
     {
         if (s.size() < b.s.size())
             return true;
         if (s.size() > b.s.size())
             return false;
         for (int i = s.size() - ; i >= ; i--)
         {
             if (s[i] < b.s[i])
                 return true;
             if (s[i] > b.s[i])
                 return false;
         }
         return false;
     }
     bool operator>=(const Big &b)
     {
         return !(*this < b);
     }
     bool operator==(const Big &b)
     {
         if (s.size() != b.s.size())
             return false;
         for (int i = ; i < s.size(); i++)
             if (s[i] != b.s[i])
                 return false;
         return true;
     }
     Big operator+(const Big &b)
     {
         Big c;
         c.s.clear();
         for (int i = , g = ;; i++)
         {
             if (g ==  && i >= s.size() && i >= b.s.size())
                 break;
             int x = g;
             if (i < s.size())
                 x += s[i];
             if (i < b.s.size())
                 x += b.s[i];
             c.s.push_back(x % BASE);
             g = x / BASE;
         }
         return c;
     }
     Big operator-(const Big &b)
     {
         Big c;
         c = *this;
         for (int i = ; i < c.s.size(); i++)
         {
             int tmp;
             if (i >= b.s.size())
                 tmp = ;
             else
                 tmp = b.s[i];
             if (c.s[i] < tmp)
             {
                 c.s[i + ] -= ;
                 c.s[i] += BASE;
             }
             c.s[i] -= tmp;
         }
         while (c.s.back() ==  && c.s.size() > )
             c.s.pop_back();
         return c;
     }
     void operator-=(const Big &b)
     {
         *this = *this - b;
     }
     Big operator*(const Big &b)
     {
         Big c;
         c.s.resize(s.size() + b.s.size());
         for (int i = ; i < s.size(); i++)
             for (int j = ; j < b.s.size(); j++)
                 c.s[i + j] += s[i] * b.s[j];
         for (int i = ; i < c.s.size() - ; i++)
         {
             c.s[i + ] += c.s[i] / BASE;
             c.s[i] %= BASE;
         }
         while (c.s.back() ==  && c.s.size() > )
             c.s.pop_back();
         return c;
     }
     friend istream &operator>>(istream &input, Big &x)
     {
         string s;
         if (!(input >> s))
             return input;
         x = s;
         return input;
     }
     friend ostream &operator<<(ostream &output, const Big &x)
     {
         output << x.s.back();
         for (int i = x.s.size() - ; i >= ; i--)
         {
             char buf[];
             sprintf(buf, "%08d", x.s[i]);
             for (int j = ; j < strlen(buf); j++)
                 output << buf[j];
         }
         return output;
     }
 };
 Big Copy(const Big &b, int x)
 {
     Big t;
     t.s.resize(b.s.size() + x);
     for (int i = ; i < b.s.size(); i++)
         t.s[i + x] = b.s[i];
     return t;
 }
 Big Divide(const Big &a, const Big &b, Big &mod)
 {
     Big c;
     c.s.resize(a.s.size() - b.s.size() + );
     mod = a;
     int Pow[(int)log2(Big::BASE) + ];
     Pow[] = ;
     for (int i = ; i <= log2(Big::BASE); i++)
         Pow[i] = Pow[i - ] * ;
     for (int i = c.s.size() - ; i >= ; i--)
     {
         Big t;
         t = Copy(b, i);
         for (int j = log2(Big::BASE); j >= ; j--)
             if (mod >= t * Pow[j])
             {
                 c.s[i] += Pow[j];
                 mod -= t * Pow[j];
             }
     }
     while (c.s.back() ==  && c.s.size() > )
         c.s.pop_back();
     return c;
 }
 Big a, b;
 int main()
 {
     cin >> a >> b;
     if (a < b)
         cout << a + b << endl << '-' << b - a << endl<< a * b << endl <<  << endl << a << endl;
     else
     {
         Big c, d;
         c = Divide(a, b, d);
         cout << a + b << endl << a - b << endl << a * b << endl << c << endl << d << endl;
     }
     return ;
 }

高精度

二十一. 最大公约数和最小公倍数

 int gcd(int a, int b) { return b ==  ? a : gcd(b, a % b); }
 int lcm(int a,int b)
 {
     a * b / gcd(a, b);
 }

二十二.简单乘法（防止因为乘数过大而爆long long）和快速幂

 int muti(int a,int b)//乘法，防止乘数太大爆long long
 {
     int ans=;
     while(b)
     {
         if(b&)
         {
             ans=(ans+a)%mod;
         }
         a=(a+a)%mod;
         b>>=;
     }
     return ans;
 }
 int KSM(int a,int b)//快速幂
 {
     int ans=;
     while(b)
     {
         if(b&)
         {
             ans=nuti(ans,a);
         }
         a=muti(a,a);
         b>>=;
     }
     return ans;
 }

二十三.质因数分解

 int devide(int x)//质因数分解
 {
     for(int i=;i<=sum&&prime[i]*prime[i]<=x;++i)
     {
         while(x%prime[i]==)
         {
             x/=prime[i];
             cout<<prime[i]<<" ";
         }
     }
     if(x!=)
     {
         cout<<x<<" ";
     }

 }

二十四.拓展欧里几德

 void exgcd(int a,int b,int &x,int &y)//拓展欧里几德
 {
     if(!b)
     {
         x=;
         y=;
         return ;
     }
     exgcd(b,a%b,y,x);
     y-=a/b*x;
 } 

二十五.逆元的几种求法

• 快速幂版

inv=KSM(x,Mod-);//逆元 (快速幂版）

• 拓展欧里几德版

exgcd(x,Mod,inv,y); inv=(inv+Mod)%Mod; //（x必须与mod互质）

• 线性求逆元，公式版

 inv[]=;//线性公式
 for(i=;i<=n;++i)
     inv[i]=1ll*(Mod-Mod/i)*inv[Mod%i]%Mod; 

二十六.floyd

 int floyd()
 {
     for(int k=;k<=n;k++)
     {
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=n;j++)
             {
                 a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
             }
         }
     }
 }

二十七·最短路之几个瞎搞模板

 void spfa(int s)
 {
     int x, y, i;
     memset(dis, 0x3f, sizeof(dis));
     queue<int> q;
     q.push(s);
     dis[s] = ;
     while (!q.empty())
     {
         x = q.front();
         q.pop();
         vis[x] = false;
         for (i = head[x]; i; i = way[i].next)
         {
             y = way[i].to;
             if (dis[y] > dis[x] + way[i].value)
             {
                 dis[y] = dis[x] + way[i].value;
                 if (!vis[y])
                 {
                     q.push(y);
                     vis[y] = true;
                 }
             }
         }
     }
 }

spfa

 priority_queue<pair<int, int>> q;
 void dijkstra(int s)
 {
     int x, y, i;
     memset(dis, 0x3f, sizeof(dis));
     q.push(make_pair(, s));
     dis[s] = ;
     while (!q.empty())
     {
         x = q.top().second;
         q.pop();
         for (i = head[x]; i; i = way[i].next)
         {
             y = way[i].to;
             if (dis[y] > dis[x] + way[i].value)
             {
                 dis[y] = dis[x] + way[i].value;
                 q.push(make_pair(-dis[y], y));
             }
         }
     }
 }

dijkstra

二十八· 二分集合

 int l = ;
     int r = maxx;
     while (l < r)
     {
         int mid = (l + r) >> ;
         if (check(mid))
         {
             r = mid;
         }
         else
         {
             l = mid + ;
         }
     }

二分最小值

 while (l < r)
     {
         int mid = (l + r) >> ;
         if (check(mid))
         {
             l = mid;
         }
         else
         {
             r = mid - ;
         }
     }

二分最大值

 while (l + eps < r)
     {
         double mid = (l + r) >> ;
         if (check(mid))
         {
             r = mid;
         }
         else
         {
             l = mid;
         }
     }

实数域二分

二十九· 树状数组求逆序对个数

    for (int i = ; i <= n; ++i)
     {
         cin >> x;
         add(x, );
         ans += i - sum(x);
     }

树状数组求逆序对

三十·01背包

 for (i = ; i <= n; ++i)//背包 n为物品数，m为物品体积
     {
         cin >> v >> w;
         for (j = m; j >= v; --j)
             f[j] = max(f[j], f[j - v] + w);
     }
     cout << f[m] << endl;

01背包

三十一·完全背包

  for (i = ; i <= n; ++i)
     {
         cin >> v >> w; //背包 n为物品数，m为物品体积
         for (j = v; j <= m; ++j)
             f[j] = max(f[j], f[j - v] + w);
     }
     cout << f[m] << endl;

完全背包

三十二 ·最长上升子序列

 d[k = ] = a[];//a是原序列，n为长度，k为最长上升子序列的长度
     for (i = ; i <= n; ++i)
     {
         if (d[k] < a[i])
             d[++k] = a[i];
         else
             d[lower_bound(d + , d + k + , a[i]) - d] = a[i];
     }
     cout << k << endl;

最长上升子序列

三十三·最长公共子序列长度

 for (i = ; i <= n; ++i)//串为a b,长度为n m
     {
         for (j = ; j <= m; ++j)
         {
             if (A[i] == B[j])
                 f[i][j] = f[i - ][j - ] + ;
             else
                 f[i][j] = max(f[i - ][j], f[i][j - ]);
         }
     }
     cout << f[n][m] << endl;

最长公共子序列

三十三·最长公共上升子序列

 B[] = -inf;//一切概念均同上；
     for (i = ; i <= n; ++i)
     {
         if (B[] < A[i])
             num = f[i - ][];
         for (j = ; j <= m; ++j)
         {
             if (A[i] == B[j])
                 f[i][j] = num + ;
             else
                 f[i][j] = f[i - ][j];
             if (B[j] < A[i])
                 num = max(num, f[i - ][j]);
         }
     }
     int ans = -inf;
     for (i = ; i <= m; ++i)
         ans = max(ans, f[n][i]);
     printf("%d", ans);

最长公共上升子序列

三十四· 倍增求LCA（必背，容易打错，一定要return）

 int pre() //LCA
 {
     for (int j = ; j <= ; j++)
     {
         for (int i = ; i <= n; i++)
         {
             fa[i][j] = fa[fa[i][j - ]][j - ];
         }
     }
 }
 int lca(int x)
 {
     int i;
     if (deep[x] < deep[y])
     {
         swap(x, y);
     }
     for (int i = ; ~i; --i)
     {
         if (deep[fa[x][i]] >= deep[y])
         {
             x = fa[x][i];
         }
     }
     if (x == y)
     {
         return x;
     }
     for (int i = ; ~i; --i)
     {
         if (fa[x][i] != fa[y][i])
         {
             x = fa[x][i];
             y = fa[y][i];
         }
     }
     return fa[x][];
 }

LCA

三十五·树的直径（两次dfs就可以了）

 int dfs(int x) //树的直径 只要两次dfs就可以了。
 {
     int i, j;
     if (ans < d[x])
     {
         ans = d[x];
         p = x;
     }
     for (int i = head[x]; i; i = way[i].next)
     {
         j = v[i];
         if (j != father)
         {
             d[j] = d[x] += w[i];
             dfs(j, x);
         }
     }
 }
 void solve()
 {
     ans = ;
     d[] = ;
     dfs(, );
     ans = ;
     d[p] = ;
     dfs(p, );
     cout << ans << endl;
 }

树的直径

三十六·树的重心

 void dfs(int x, int father)//树的重心
 {
     int i, j;
     Max[x] = , size[x] = ;
     for (i = head[x]; i; i = way[i].next)
     {
         j = way[i].to;
         if (j != father)
         {
             dfs(j, x);
             size[x] += size[j];
             Max[x] = max(Max[x], size[j]);
         }
     }
     Max[x] = max(Max[x], n - size[x]);
     if (num > Max[x])
     {
         pos = x;
         num = Max[x];
     }
 }

树的重心

三十七·LCA树链剖分版，要稳定一些

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 const int maxn = 5e5 + ;

 int num, size[maxn], deep[maxn], fa[maxn], top[maxn], n, m, p, a, b;
 struct node
 {
     int to;
     int value;
     int next;
 }way[maxn<<];
 int tot = ;
 int head[maxn];
 int add(int x,int y)
 {
     way[++tot].next = head[x];
     way[tot].to = y;
     head[x] = tot;
 }
 int dfs1(int x)
 {
     size[x] = ;
     deep[x] = deep[fa[x]] + ;
     for (int i = head[x]; i;i=way[i].next)
     {
         if(fa[x]!=way[i].to)
         {
             fa[way[i].to] = x;
             dfs1(way[i].to);
             size[x] += size[way[i].to];
         }
     }
 }
 int dfs2(int x)
 {
     int maxx = ;
     if(!top[x])
     {
         top[x] = x;
     }
     for (int i = head[x]; i;i=way[i].next)
     {
         if (fa[x] != way[i].to && size[way[i].to] > size[maxx])
         {
             maxx = way[i].to;
         }
     }
     if(maxx)
     {
         top[maxx] = top[x];
         dfs2(maxx);
     }
     for (int i = head[x]; i; i = way[i].next)
     {
         if(way[i].to!=maxx&&fa[x]!=way[i].to)
         {
             dfs2(way[i].to);
         }
     }
 }
 int lca(int x,int y)
 {
     while(top[x]!=top[y])
     {
         if(deep[top[x]]<deep[top[y]])
         {
             swap(x, y);
         }
         x = fa[top[x]];
     }
     if(deep[x]<deep[y])
     {
         return x;
     }
     return y;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin >> n >> m >> p;
     for (int i = ; i < n;i++)
     {
         cin >> a >> b;
         add(a, b);
         add(b, a);
     }
     dfs1(p);
     dfs2(p);
     for (int i = ; i <= m;i++)
     {
         cin >> a >> b;
         cout << lca(a, b) << endl;
     }
     return ;
 }

LCA

三十八·字典树

• 存树

 struct node
 {
     int son[];
     int num;
 } a[maxn];

• 插入

 void Insert()
 {
     int l, i, p = ;
     l = strlen(s);
     for (i = ; i < l; ++i)
     {
         if (a[p].son[s[i] - 'a'] == )
             a[p].son[s[i] - 'a'] = ++t;
         p = a[p].son[s[i] - 'a'];
         a[p].num++;

     }
 }

• 查询

 int find()
 {
     int l, i, p = ;
     l = strlen(s);
     for (i = ; i < l; ++i)
     {
         if (a[p].son[s[i] - 'a'] == )
             return ;
         p = a[p].son[s[i] - 'a'];
     }
     return a[p].num;
 }

三十九· 字符串hash

 long long Hash()//base 是基数 ans 是hash值 l是长度 s[i]是第i个字符
 {
     long long  ans = ;
     for (int i = ; i < l; ++i)
         ans = ans * base + s[i];
     return ans;
 }

四十·线段树1

 #include<iostream>
 using namespace std;
 const int maxn = 1e6 + ;
 int a[maxn + ];
 struct node
 {
     int l, r;
     long long pre, add;
 } tree[maxn];

 void build(int x,int l,int r)
 {
     tree[x].l = l;
     tree[x].r = r;
     if(l==r)
     {
         tree[x].pre = a[l];
         return;
     }
     int mid = (l + r) >> ;
     build(x * , l, mid);
     build(x *  + , mid + , r);
     tree[x].pre = tree[x * ].pre + tree[x *  + ].pre;
 }
 void spread(int p)
 {
     if (tree[p].add)
     {
         tree[p * ].pre += tree[p].add * (tree[p * ].r - tree[p * ].l + );
         tree[p *  + ].pre += tree[p].add * (tree[p *  + ].r - tree[p *  + ].l + );
         tree[p * ].add += tree[p].add;
         tree[p *  + ].add += tree[p].add;
         tree[p].add = ;
     }
 }
 void add(int p, int x, int y, int z)
 {
     if (x <= tree[p].l && y >= tree[p].r)
     {
         tree[p].pre += (long long)z * (tree[p].r - tree[p].l + );
         tree[p].add += z;
         return;
     }
     spread(p);
     int mid = tree[p].l + tree[p].r >> ;
     if (x <= mid)
         add(p * , x, y, z);
     if (y > mid)
         add(p *  + , x, y, z);
     tree[p].pre = tree[p * ].pre + tree[p *  + ].pre;
 }
 long long sum(int p, int x, int y)
 {
     if (x <= tree[p].l && y >= tree[p].r)
         return tree[p].pre;
     spread(p);
     int mid = tree[p].l + tree[p].r >> ;
     long long ans = ;
     if (x <= mid)
         ans += sum(p * , x, y);
     if (y > mid)
         ans += sum(p *  + , x, y);
     return ans;
 }
 int main()
 {
     int n, m;
     cin >> n >> m;
     for (int i = ;i<=n;i++)
     {
         cin >> a[i];
     }
     build(, , n);
     for (int i = ;i<=m;i++)
     {
         int q, x, y, z;
         cin >> q;
         if(q==)
         {
             cin >> x >> y >> z;
             add(, x, y, z);
         }
         else
         {
             cin >> x >> y;
             cout << sum(, x, y) << endl;
         }
     }
     return ;
 }

四十一·矩阵快速幂

 #include <iostream>
 #include <cstring>
 #define mod 1000000007
 #define ll long long
 using namespace std;
 struct Mat
 {
     ll m[][];
 };
 Mat a, e;
 ll n, p;
 Mat Mul(Mat x, Mat y)
 {
     Mat c;
     for (int i = ; i <= n; i++)
     {
         for (int j = ; j <= n; j++)
         {
              c.m[i][j] = ;
         }
     }
     for (int i = ; i <= n; i++)
     {
         for (int j = ; j <= n; j++)
         {
              for (int k = ; k <= n; k++)
              {
                  c.m[i][j] = c.m[i][j] % mod + x.m[i][k] * y.m[k][j] % mod;
              }
         }
     }
     return c;
 }
 Mat pow(Mat x, ll y)
 {
     Mat ans = e;
     while (y)
     {
         if (y & )
             ans = Mul(ans, x);
         x = Mul(x, x);
         y >>= ;
     }
     return ans;
 }

 int main()
 {
     cin >> n >> p;
     for (int i = ; i <= n; i++)
     {
         for (int j = ; j <= n; j++)
         {
             cin >> a.m[i][j];
         }
     }
     for (int i = ; i <= n; i++)
     {
         e.m[i][i] = ;
     }
     Mat ans = pow(a, p);
     for (int i = ; i <= n; i++)
     {
         for (int j = ; j <= n; j++)
         {
             cout << ans.m[i][j] % mod << " ";
         }
         cout << endl;
     }
     return ;
 }

四十二·退役前最后的一次更新  进制转换，10 转其他

 #include<iostream>
 #include<cstdio>
 using namespace std;
 int n,m;
 char f[] = {'', '', '', '', '', '', '', '', '', '', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J'};
 void  zhuan(int n,int m)
 {
     if(n==)
     {
         return;
     }
     if(n>||n%m==)
     {
         zhuan(n / m, m);
         cout << f[n % m];
     }
     else
     {
         zhuan(n / m + , m);
         cout << f[-m+n % m];
     }

 }
 int main()
 {
     cin >> n;
     cin >> m;
     cout << n << "=";
     zhuan(n, m);
     cout << "(base" << m << ")" << endl;
     return ;
 }