鸽巢原理及其扩展——Ramsey定理

第一部分：鸽巢原理

咕咕咕！！！

然鹅大家还是最熟悉我→

a数组：but 我也很重要

$：我好像也出现不少次

以上纯属灌水

---

文章简叙：鸽巢原理对初赛时的问题求解以及复赛的数论题目都有启发意义。直接的初赛考察一般在提高组出现。相当于抽屉。

别名：鸽笼原理。狄利克雷抽屉原理。

最简单的一种形式：有m+1m+1m+1只鸽子，mmm个笼子，那么至少有一个笼子有至少两只鸽子。当然，换个角度来说：有m−1m-1m−1只鸽子，mmm个笼子，那么至少有一个笼子是空的。

初级加强：有mmm个笼子，k∗m+1k*m+1k∗m+1只鸽子，那么至少有一个笼子有至少k+1k+1k+1只鸽子。

高级加强：令

• a1,a2,a3...ama_1,a_2,a_3...a_ma1​,a2​,a3​...am​

• 为正整数。

• ififif 我们将

• a1+a2+a3+...+an−n+1a_1+a_2+a_3+...+a_n-n+1a1​+a2​+a3​+...+an​−n+1

• 个鸽子放入nnn个笼子里，thenthenthen，

||第一个笼子至少有a1a_1a1​只鸽子||第二个笼子至少有a2a_2a2​只鸽子||第三个笼子至少有a3a_3a3​只鸽子||…||第mmm个笼子至少有ama_mam​只鸽子

---

鸽巢原理的应用

一位洛谷oieroieroier要用121212周的时间准备  CTSC  ~~CTSC~~  CTSC  ,为了练习，他每天至少要刷一题，因为题目有难度，他每星期刷题无法超过131313题。请你证明：存在连续的若干天期间，这位oieroieroier恰好刷了111111题

开始证明：

1.我们可以令a1a_1a1​表示第一天所刷的题数，a2a_2a2​表示前两天所刷的题数，a3a_3a3​表示前三天所刷的题数.之后以此类推

2.而题目说，由于每天都要至少刷1题，所以数列

• a1,a2,a3,a4,...,a84a_1,a_2,a_3,a_4,...,a_{84}a1​,a2​,a3​,a4​,...,a84​

• 严格递增。另有a1&gt;=1a_1&gt;=1a1​>=1.又每周最多刷13题，故a84&lt;=13∗12=156a_{84}&lt;=13*12=156a84​<=13∗12=156.

3.因此又有：

• 1&lt;=a1&lt;a2&lt;a3&lt;...&lt;a84&lt;=1561&lt;=a_1&lt;a_2&lt;a_3&lt;...&lt;a_{84}&lt;=1561<=a1​<a2​<a3​<...<a84​<=156.

4.同理，

• a1+11,a2+11,a3+11,...,a84+11a_1+11,a_2+11,a_3+11,...,a_{84}+11a1​+11,a2​+11,a3​+11,...,a84​+11

• 同样是一个严格递增序列。范围：

• 12&lt;=a1+11&lt;a2+11&lt;a3+11&lt;...&lt;a84+11&lt;=16712&lt;=a_1+11&lt;a_2+11&lt;a_3+11&lt;...&lt;a_{84}+11&lt;=16712<=a1​+11<a2​+11<a3​+11<...<a84​+11<=167

5.我们把两个序列合起来看：

• a1,a2,a3,...,a84,a1+11,a2+11,a3+11,...,a84+11a_1,a_2,a_3,...,a_{84},a_1+11,a_2+11,a_3+11,...,a_{84}+11a1​,a2​,a3​,...,a84​,a1​+11,a2​+11,a3​+11,...,a84​+11

• 一共168168168个数。其中每一个数都是111到167167167之间的一个整数。

6.根据鸽巢原理可得，其中必有两个数相等！！！

7.既然

• a1,a2,a3,...,a84a_1,a_2,a_3,...,a_{84}a1​,a2​,a3​,...,a84​

• 中必然无相等的两个数，

• 那么a1+11,a2+11,a3+11,...,a84+11a_1+11,a_2+11,a_3+11,...,a_{84}+11a1​+11,a2​+11,a3​+11,...,a84​+11

• 中同理。那么，必然存在一个xxx和一个yyy,使得

• ax=ay+11a_x=a_y+11ax​=ay​+11;

8.从而得出结论：这个oieroieroier在第

• y+1,y+2,y+3,...,xy+1,y+2,y+3,...,xy+1,y+2,y+3,...,x

• 天内一共刷了111111道题

---

应用二

证明：在边长为222的等边三角形中放上555个点。则至少存在两个点，他们之间的距离小于等于111.

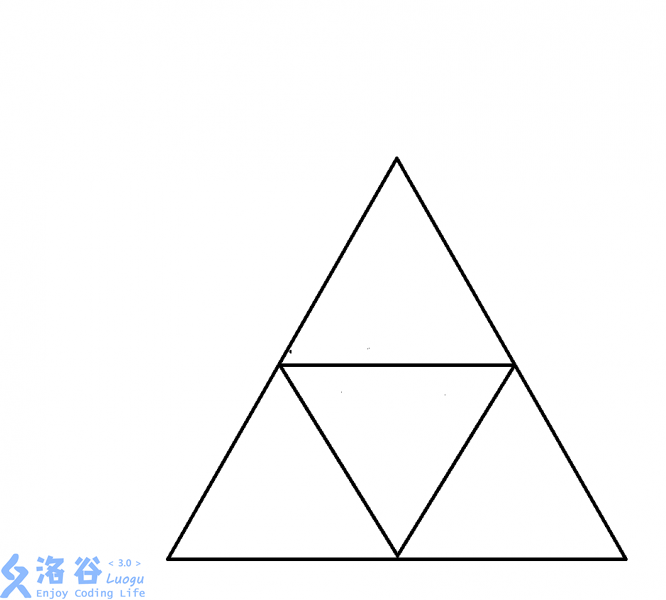
1.我们先画出一个边长为222的等边三角形。

2.然后把三条边中点两两相连。就形成了这张图。

3.那么根据鸽巢原理，必然有两个点在一个边长为111的小三角形里。

4.而我们知道，边长为111的等边三角形里处处距离都小于等于111

5.于是问题就解决了

---

应用三

已知n+1n+1n+1个正整数，它们全都小于或等于2n2n2n，证明当中一定有两个数是互质的。

1.要证明这个问题，我们就要利用一个互质的特性：两个相邻整数互质。

2.有了这个突破口，于是我们可以构造n个鸽巢，每一个里依次放入

• 1,2,3,...,2n1,2,3,...,2n1,2,3,...,2n

• 这2n个数中的两个数。

3.也就是说，我们要在这其中取出n+1n+1n+1个数。

4.根据鸽巢原理，无论如何，我们都会抽空一个鸽巢。

5.一个鸽巢中的两个数肯定互质，所以问题就解决了。

扒栗史：匈牙利大数学家厄杜斯(PaulErdous,1913 - 1996) 向当年年仅111111岁的波萨(LouisPósa)提出这个问题，而小波萨思考了不足半分钟便能给出正确的答案。

---

有趣的小（leng）知（xiao）识（hua）：

山东高考201720172017年有545454万人。而人的头发大约有8−128-128−12万根。那么必然有两人的头发数量相同。

好了，现在来一道初赛真题收（dian）心(di):

【NOIP2010 提高组】记TTT为一队列，初始时为空，现有n个总和不超过323232的正整数依次入队，如果无论这些数具体为什么值，都能找到一种出队的方式，使得存在某个时刻队列TTT中的数之和恰好为999，那么nnn的最小值是_______________

1.第一眼看到此题，蒟蒻就知道自己只能根据结果推过程了

2.刚开始看了一眼答案：181818.

3.于是就根据这个开始推导过程。我们可以令aia_iai​表示前iii个数的和，并约定：a0=0a_0=0a0​=0.

4.题目要求求出最小的nnn，使得存在0&lt;=x&lt;y&lt;=n0&lt;=x&lt;y&lt;=n0<=x<y<=n满足ay=ax+9a_y=a_x+9ay​=ax​+9;

5.于是我们可将aaa数组看做鸽子，用不能同时取的一组（差为999）的集合构造笼子，

6.构造方法如下：一共有n=18n=18n=18个集合按此方式选取：

• 0,9、1,10、2,11、...、8,17、18,27、19,28、20,29、...、23,32、24、25、26{0,9}、{1,10}、{2,11}、...、{8,17}、{18,27}、{19,28}、{20,29}、...、{23,32}、{24}、{25}、{26}0,9、1,10、2,11、...、8,17、18,27、19,28、20,29、...、23,32、24、25、26。

7.由题意可知，我们一旦在某个集合中取了两个元素，thenthenthen 一定存在某个时刻队列TTT中数的总和恰好为999.

8.于是由鸽巢原理，我们可以得知：n=18n=18n=18一定满足条件.

但是题目要让我们求出最小值，为了保险起见（都看答案了还保什么险）：

1.我们还要证明一下n=17n=17n=17不可行。

2.然鹅我们只需要举出反例即可：

• 1 1 1 1 1 1 1 1 10 1 1 1 1 1 1 1 1

3.说明：因为每到了888个111就被101010隔断，故不可行。

---

第二部分：Ramsey定理

扒栗史：此定理由Frank Plumpton Ramsey（弗兰克·普伦普顿·拉姆齐，1903−19301903-19301903−1930）提出.

• 此定理有一个广为流传的例子：6 个人中至少存在3人相互认识或者相互不认识。

• 转换：该定理等价于证明这6个顶点的完全图的边，用红、蓝二色任意着色，必然至少存在一个红色边三角形，或蓝色边三角形

证明如下：

1、首先，把这6个人设为A、B、C、D、E、F六个点。由A点可以引出AB、AC、AD、AE、AF五条线段。

2、设：如果两个人认识，则设这两个人组成的线段为红色；如果两个人不认识，则设这两个人组成的线段为蓝色。

3、由鸽巢原理可知：这五条线段中至少有三条是同色的。不妨设AB、AC、AD为红色。若BC或CD为红色，则结论显然成立。若BC和CD均为蓝色，则若BD为红色，则一定有三个人相互认识；若BD为蓝色，则一定有三个人互相不认识。

以下部分正在补充，本文未完成

后记：部分内容来自于一本通