机器学习 1 regression

Linear regerssion 线性回归

回归：

stock market forecast

f(过去10年股票起伏的资料) = 明天道琼指数点数

self driving car

f(获取的道路图像)= 方向盘角度

recommendation

f(使用者A 商品B)= 购买商品可能性

预测妙蛙种子 cp值 combat power

f( xs ) =cp after evolution

xs

xhp

xw

xh

找model

定义 function set

step 1: model

y = b+ w* xcp  进化前的CP值

f1 : y= 10.0+9*xcp

f2: y= 9.8+9.2*xcp

f3: y= -0.8-1.2*xcp

infinite 有很多

linear model : y=b+sum(wi*xi)

xi feature wi weight b bais

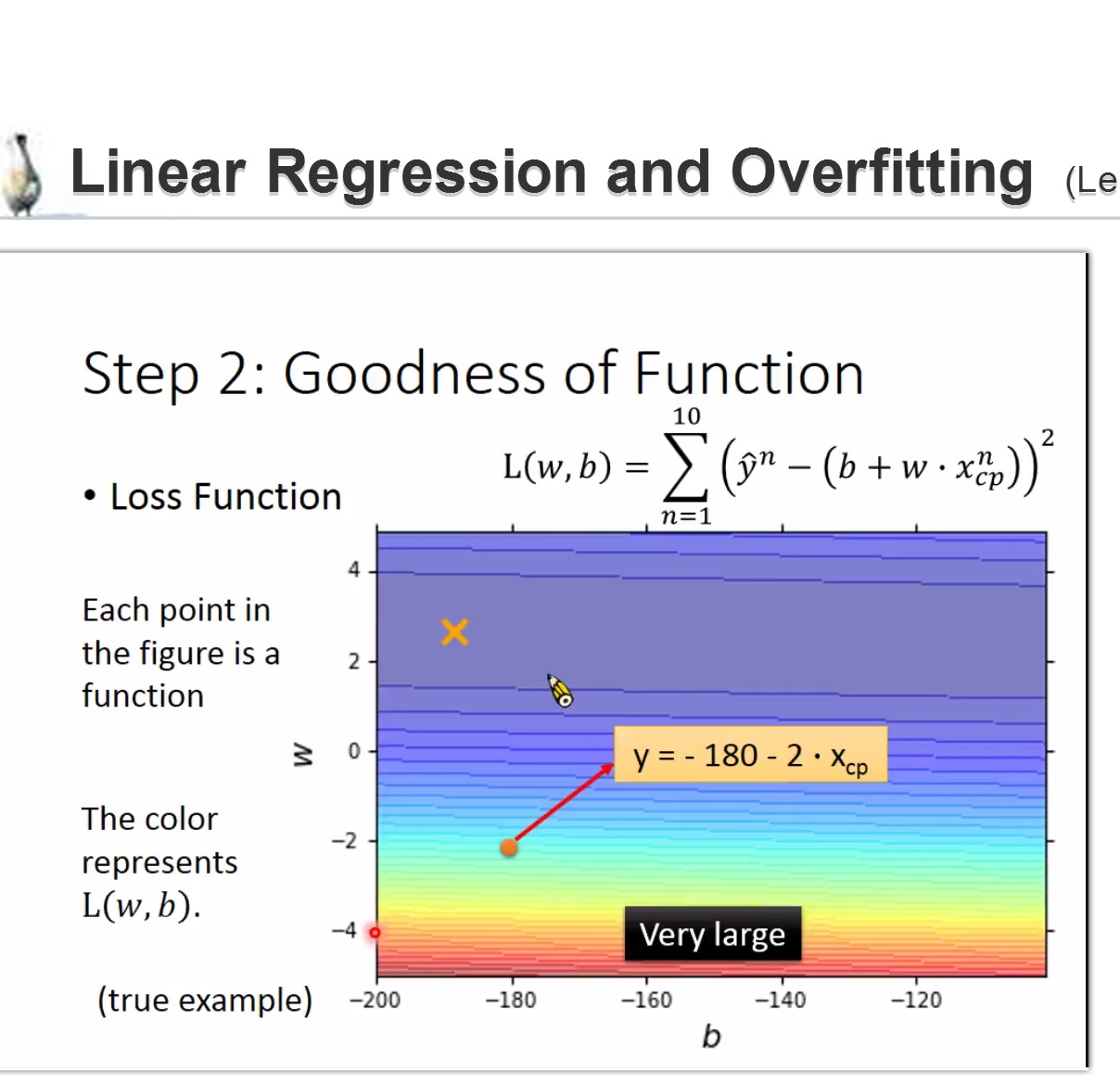
step2: goodness of function

x¹ ,   y^{^1}

x² ,   y^{^2}

...

x¹⁰ ,   y^{^10}

x 进化前的CP值

y 进化后的CP值

xⁿ_cp  

损失函数

L（f）=L(w,b)

使用某个function 的wb 用来计算L

step: best function

gradient descent

L(w) w

w*= arg min_wL(w)

穷举W所有值 ，看计算那个值？ 效率低

可以： 1） 随机选取初始点 W⁰

2) 计算 dL/dw| w=w0

也就是切线的斜率      negative -》 increase w

positive -> decrease w

往左边走一步 还是右边走，LOSS会减少？

stepsize: 却觉于

1)现在的微分值越大，也就是越陡峭，

2)还有就是常数项 learning rate

w1 <- w0- n* dl/dw|w=w0

w2 <- w1-n*dl/dw|w=w1

local optimal 会找到局部最小值，而不是global optimal

如果是两个参数？ w*,b* = arg min _w,b L(w,b)

与上面的过程一致

有两个参数 w,b 决定了function

in linear regression ,the loss function L ins convex

NO local optimal

how's the results?

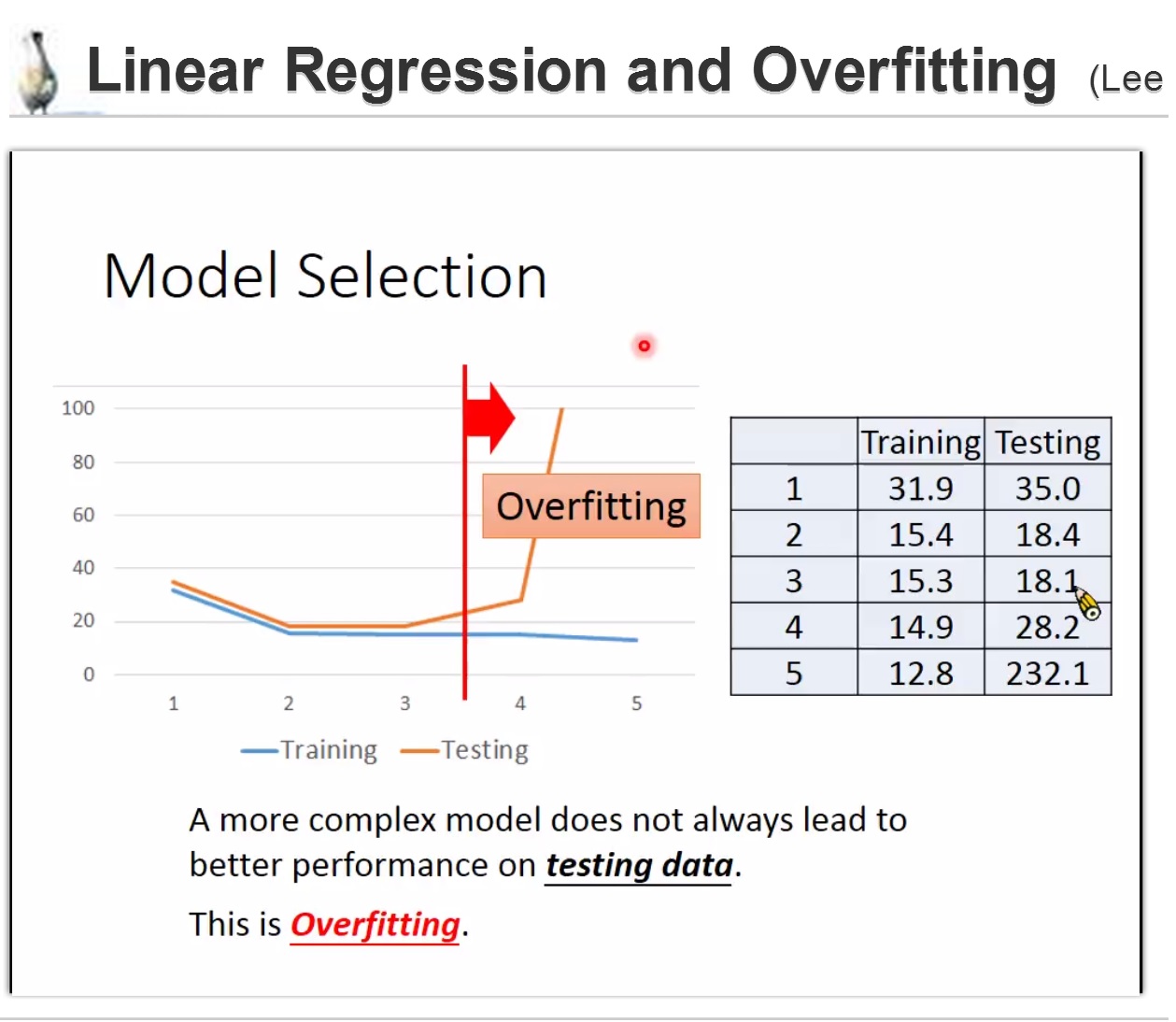
Generalization 泛化性能

selecting another model

y= b+w₁*x_cp+w₂*(x_cp)²

有没有可能更复杂的model,

how about more complex model?

在train data上效果是模型越复杂，效果很好，这是因为

越复杂的模型是包括简单的模型

A more complex model yields lower error on training data

但是在test data上效果不一定是。这就是overfitting

只考虑进化前的cp值可能还不够，同时需要考虑物种

预测重新设计function Set

if xs=pidgey y=b1+w1*x_cp

也是线性模型，不同种类的物种，它的model不一样

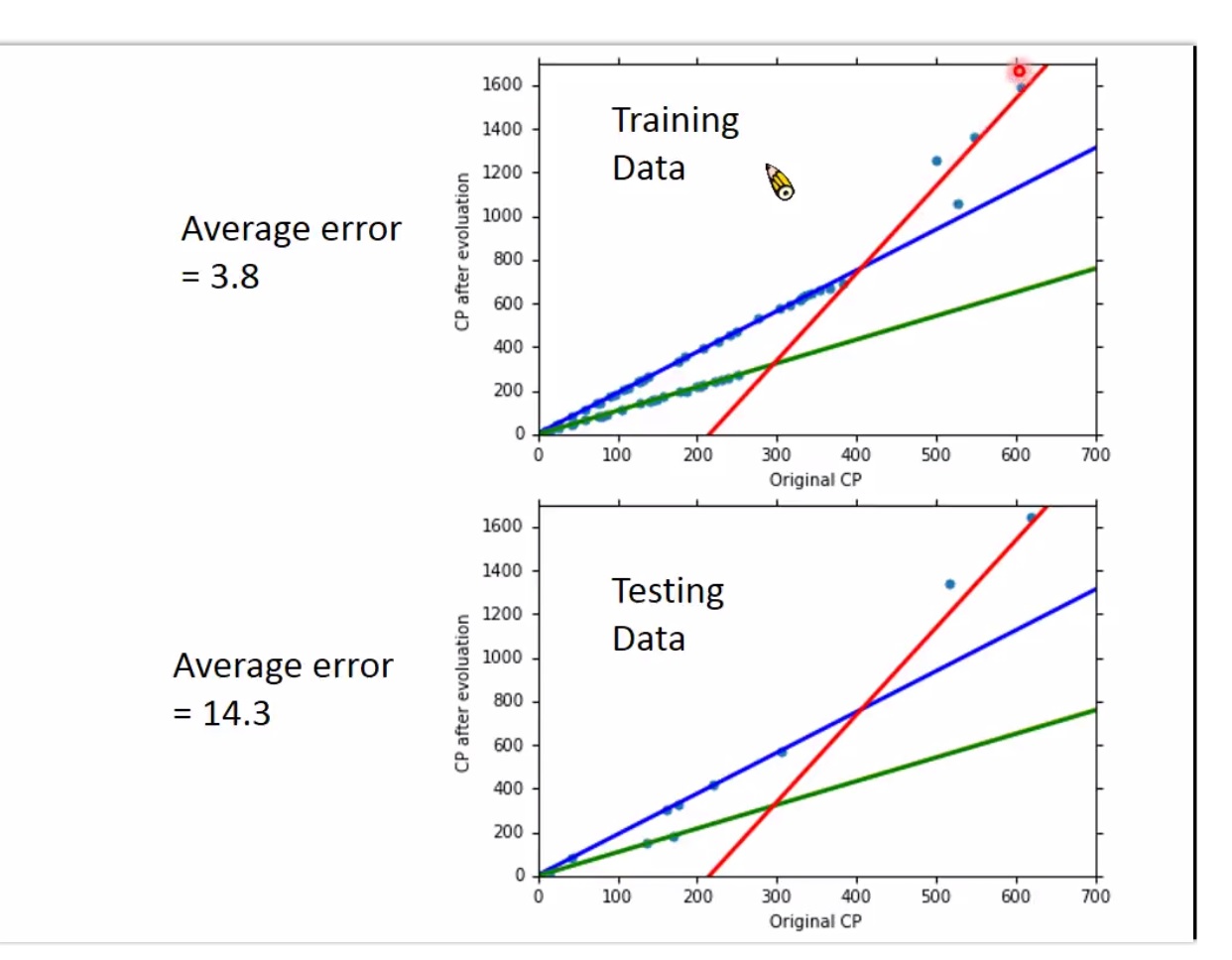
考虑其他的影响因素 用更加复杂的模型

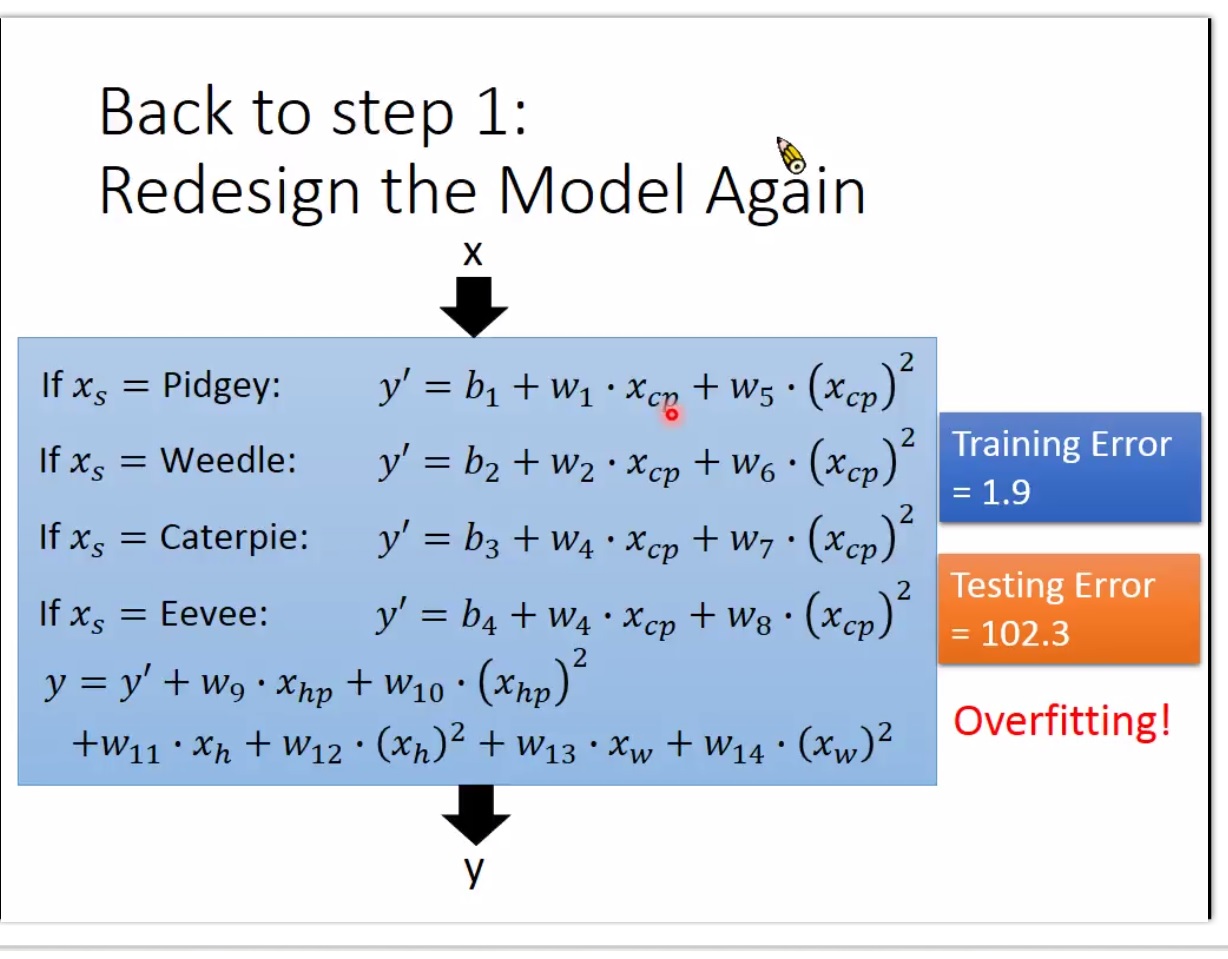
已经过拟合了

regularization 正则项 ，去解决过拟合，

当W很小，接近0，当输入有变化，output对输入变化不敏感。

输出对输入就不敏感，function 就平滑。如果一个平滑的function

收到噪声影响小。

调整b 和function平滑没关系，只是和位置有关系

lamad 越大，考虑训练误差越小

我们希望function平滑，但不能太平滑，调整lamad