matlab-层次分析法

层次分析法（AHP）是把问题条理化、层次化，构造出一个有层次的结构模型的方法。

比如要选择旅游地，有3个选择方案，苏杭、北戴河和桂林。选择过程需要考虑多个因素，比如景色、费用、居住、饮食和旅途。

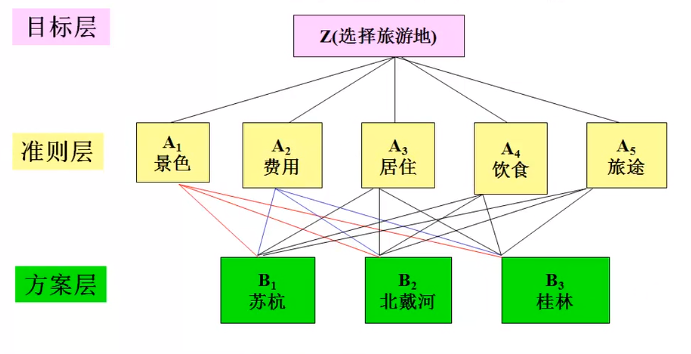
1.分为目标层（选择旅游地），准则层（景色、费用、居住、饮食和旅途）和方案层（苏杭、北戴河和桂林）。层次结构模型如图所示：

2.构造判断矩阵

标度是主观判断的，不同人造出来的矩阵可能不一样。

准则层的矩阵：A_x = [ a_ij ]; x个n*n的矩阵，此时n=5表示准则层的数量，x表示准则层对目标层的影响，这里x=1。

举例：a₁₄ = 3表示主观认为在选择旅游地时，景色比美食稍重要。反之，a₄₁ = 1/3表示美食比景色稍不重要。

方案层的矩阵：Bx = [ a_ij ]; x个n*n的矩阵，此时n=3表示方案层的数量，x表示准则层对方案层的影响，这里x=5。

举例：B₁中，a₁₃=5表示，在景色方面，苏杭比桂林明显重要。

也就是要构造x+1=6个矩阵。数据如下，是主观假设给出的。

[
 /   ;
    ;
/ /  / /;
/ /   ;
/ /
]

[
  ;
/  ;
/ /
]

[
 / /;
  /;

]

[
  ;
  ;
/ /
]

[
  ;
/  ;
/
]

[
  /;
  /;

]

数据

3.一致性检验

构造判断矩阵过程可能会构造错误，比如矩阵

1    9    1/3

9    1    5

3    1/5  1

a₁₂ = 9 表示 因素1比因素2极端重要，a₃₁=2表示因素3比因素1稍重要，则重要程度显然是 因素3>因素1>因素2，而a₂₃=5表示因素2比因素3明显重要，矛盾。

并且对于每一个n阶矩阵会得到一个权重矩阵W，W是一个n*1的矩阵，即n个数，比如A矩阵得到的W_A矩阵是

[0.26228;

0.47439;
0.054492;
0.098534;
0.1103;]

表示景色、费用、居住、饮食和旅途对于选择旅游地（上一层）的权重比分别是0.26228、0.47439、0.054492、0.098534和0.1103。体现出影响因素的层次。

比如B2得到的W_B2矩阵是

[0.08199;
0.23645;
0.68156]

表示苏杭、北戴河和桂林在景色方面的权重比分别是0.08199、0.23645和0.68156。

4.对权值计算做出决策

获得了6个矩阵的权重比，分别是

W_A=[0.26228;0.47439;0.054492;0.098534;0.1103]；

W_B1=[0.59489;0.27661;0.1285];

W_B2=[0.08199;0.23645;0.68156];

W_B3=[0.42857;0.42857;0.14286];

W_B4=[0.63275;0.1924;0.17485];

W_B5=[0.16667;0.16667;0.66667];

每一个旅游景点对于目标层Z的权重=准则层权重*方案层权重之和。

苏杭的权重=0.26228*0.59489+0.47439*0.08199+0.054492*0.42857+0.098534*0.63275+0.1103*0.16667=0.29901

北戴河的权重=0.26228*0.27661+0.47439*0.23645+0.054492*0.42857+0.098534*0.1924+0.1103*0.16667=0.24541

桂林的权重=0.26228*0.1285+0.47439*0.68156+0.054492*0.14286+0.098534*0.17485+0.1103*0.66667=0.45558

最后0.29901+0.24541+0.45558=1；

桂林的比重最大，选择去桂林！

代码：

clc
clear all;
disp('请输入判断矩阵A（n阶）');
A = input('A=');
[n,~]=size(A);%由于矩阵构造方法的原因，矩阵都是正方形的所以关于矩阵的大小只需要取一个参数
Asum=sum(A,1);%求每一列的和
Aprogress=A./(ones(n,1)*Asum);%计算每一列个元素在这一列占的比重
W=sum(Aprogress,2)./n;%每一行元素相加取平均值，需要注意这里W是个列项量且所有值加起来等于1
w=A*W;%如果A的矩阵是理想状况的话这里W=w
lam=sum(w./W)/n;%通过这一步最大lam
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45];
CI=(lam-n)/(n-1);
CR=CI/RI(n);%计算误差
if CR<0.10 %如果误差小于0.1则可以接受
	disp('此矩阵的一致性可以接受!');
    fprintf('Cl=');disp(CI);
	fprintf('CR=');disp(CR);
	fprintf('W=');disp(W);
else
	disp('此矩阵的一致性不可以接受!');
end

对于不同阶判断矩阵是否满足一致性，引入判断矩阵的平均随机一致性指标RI(rand index)。Saaty给出的RI的值是一连串系数，对应各阶矩阵分别

1阶和2阶会提示不满足一致性检验，但只要矩阵斜对称就可以了。因为RI(1)和RI(2)都等于0，导致CR为NaN不能进入if语句。但是可以求出权重比W。

B站视频看到的矩阵数据，但是RI数组和我不一样。我的RI数组是在建模神书司守奎的算法大全上看的。

https://www.bilibili.com/video/av29474522/?p=2