容斥原理--计算并集的元素个数 URAL 1091

在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。　　【百度百科】

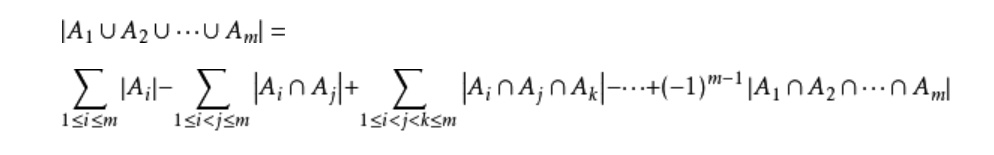
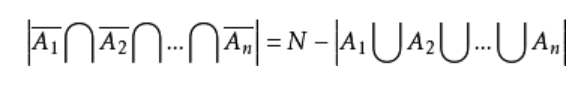
通常我们遇到的题多是(A1∪A2)=A1+A2-A1∩A2和A1∩A2=A1+A2-(A1∪A2)。

例题：URAL 1091

Tmutarakan Exams

URAL - 1091

University of New Tmutarakan trains the first-class specialists in mental arithmetic. To enter the University you should master arithmetic perfectly. One of the entrance exams at the Divisibility Department is the following. Examinees are asked to find K different numbers that have a common divisor greater than 1. All numbers in each set should not exceed a given number S. The numbers K and S are announced at the beginning of the exam. To exclude copying (the Department is the most prestigious in the town!) each set of numbers is credited only once (to the person who submitted it first).

Last year these numbers were K=25 and S=49 and, unfortunately, nobody passed the exam. Moreover, it was proved later by the best minds of the Department that there do not exist sets of numbers with the required properties. To avoid embarrassment this year, the dean asked for your help. You should find the number of sets of K different numbers, each of the numbers not exceeding S, which have a common divisor greater than 1. Of course, the number of such sets equals the maximal possible number of new students of the Department.

Input

The input contains numbers K and S (2 ≤ K ≤ S ≤ 50).

Output

You should output the maximal possible number of the Department's new students if this number does not exceed 10000 which is the maximal capacity of the Department, otherwise you should output 10000.

Example

input	output
3 10	11

题意：

输入K,S,问对于从集合{1，2，3......S}中选出K个数字，使他们的最大公因数大于1，这样的选法有几个？

分析:

可以参考素数筛的思想，我们先选出一个质数，那么这个质数的倍数和这个质数组成的集合，他们的最大公因数一定是这个质数本身，假设选取的质数是i，那么1~s有[(s-i)/i+1]个数是i的倍数，从这些数中选出k个数是一定满足条件的，所以我们可以枚举1~s所有的质数，然后有ans+=C([s-i]/i+1,k)。

但是我们发现：以2为例可以得到6,12,18，以3为例也可以得到6,12,18，不同质数的倍数可能会相同！假如k正好是2，那么选择2的倍数中的6，12和选择3的倍数中的6，12就会导致重复计算，所以我们要减去重复计算的部分。

我们只要在枚举的过程中判断一下当前枚举的数是不是两个质数之积，如果是，设i是两个质数之积，同理，我们从i的所有倍数中选出k个数，有C([s-i]/i+1,k)种选法，然后ans-=C([s-i]/i+1,k)即可。

AC code:

#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
bool u[];
ll su[];
ll c[][];
ll num,s,k;
void olas()
{
    memset(u,true,sizeof(u));
    num=;
    u[]=u[]=false;
    for(ll i=;i<=;i++)
    {
        if(u[i])    su[num++]=i;
        for(ll j=;j<num;j++)
        {
            if(i*su[j]>)    break;
            u[i*su[j]]=false;
            if(i%su[j]==)    break;
        }
    }
}
void cal_C()
{
    for(ll i=;i<=;i++)    c[i][]=;
    for(ll i=;i<=;i++)
        for(ll j=;j<=;j++)
            c[i][j]=c[i-][j]+c[i-][j-];
}
bool pxp(ll x)
{
    for(ll i=;i<=;i++)
    {
        if(x%i==&&u[i]&&i!=x/i&&u[x/i])
            return true;
    }
    return false;
}
ll work()
{
    ll ans=;
    for(ll i=;i<=s;i++)
    {
        if(u[i])
        {
            ans+=c[(s-i)/i+][k];
        }
        else if(pxp(i))
        {
            ans-=c[(s-i)/i+][k];
        }
    }
    return ans>?:ans;
}
int main()
{
    //freopen("input.txt","r",stdin);
    olas();
    cal_C();
    scanf("%lld%lld",&k,&s);
    printf("%lld\n",work());
    return ;
}