CF #365 DIV2 D Mishka and Interesting sum 区间异或+线段树

D. Mishka and Interesting sum

time limit per test

3.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Mishka enjoys programming. Since her birthday has just passed, her friends decided to present her with array of non-negative integers a1, a2, ..., an of n elements!

Mishka loved the array and she instantly decided to determine its beauty value, but she is too little and can't process large arrays. Right because of that she invited you to visit her and asked you to process m queries.

Each query is processed in the following way:

1. Two integers l and r (1 ≤ l ≤ r ≤ n) are specified — bounds of query segment.
2. Integers, presented in array segment [l,  r] (in sequence of integers al, al + 1, ..., ar) even number of times, are written down.
3. XOR-sum of written down integers is calculated, and this value is the answer for a query. Formally, if integers written down in point 2 are x1, x2, ..., xk, then Mishka wants to know the value , where  — operator of exclusive bitwise OR.

Since only the little bears know the definition of array beauty, all you are to do is to answer each of queries presented.

Input

The first line of the input contains single integer n (1 ≤ n ≤ 1 000 000) — the number of elements in the array.

The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — array elements.

The third line of the input contains single integer m (1 ≤ m ≤ 1 000 000) — the number of queries.

Each of the next m lines describes corresponding query by a pair of integers l and r (1 ≤ l ≤ r ≤ n) — the bounds of query segment.

Output

Print m non-negative integers — the answers for the queries in the order they appear in the input.

Examples

input

3
3 7 8
1
1 3

output

0

input

7
1 2 1 3 3 2 3
5
4 7
4 5
1 3
1 7
1 5

output

0
3
1
3
2

Note

In the second sample:

There is no integers in the segment of the first query, presented even number of times in the segment — the answer is 0.

In the second query there is only integer 3 is presented even number of times — the answer is 3.

In the third query only integer 1 is written down — the answer is 1.

In the fourth query all array elements are considered. Only 1 and 2 are presented there even number of times. The answer is .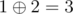

In the fifth query 1 and 3 are written down. The answer is .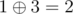

题意：给你n个数字，<=1e9，接下来m个询问。每次询问包括l,r两个数，询问从l到r的区间内，出现次数为奇数个的数字的异或和。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <map>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <algorithm>
using namespace std;
typedef  long long  ll;
typedef unsigned long long ull;
#define MM(a,b) memset(a,b,sizeof(a));
#define inf 0x7f7f7f7f
#define FOR(i,n) for(int i=1;i<=n;i++)
#define CT continue;
#define PF printf
#define SC scanf
const int mod=1000000007;
const int N=1e6+100;
int n,m,c[N],pre[N],sum[N],a[N],ans[N];

struct node{
   int l,r,pos;
}ne[N];

int lowbit(int i)
{
    return i&(-i);
}

void add(int p,int u)
{
    while(p<=n)
    {
        c[p]^=u;
        p+=lowbit(p);
    }
}

int query(int u)
{
   int res=0;
   while(u>=1)
   {
       res^=c[u];
       u-=lowbit(u);
   }
   return res;
}

bool cmp(node a,node b)
{
    return a.r<b.r;
}

map<int,int> mp;
int main()
{
    while(~scanf("%d",&n))
    {
        MM(sum,0);MM(pre,0);MM(c,0);
        mp.clear();
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            sum[i]=sum[i-1]^a[i];
            if(mp[a[i]]) pre[i]=mp[a[i]];
            mp[a[i]]=i;
        }
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d",&ne[i].l,&ne[i].r);
            ne[i].pos=i;
        }
        sort(ne+1,ne+m+1,cmp);
        int i=1;
        for(int k=1;k<=m;k++)
        {
            for(;i<=ne[k].r;i++)
            {
                if(pre[i]) add(pre[i],a[i]);
                add(i,a[i]);
            }
            ans[ne[k].pos]=(query(ne[k].r)^query(ne[k].l-1)^sum[ne[k].r]^sum[ne[k].l-1]);
        }
        for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
    }
    return 0;
}

　　比赛分析：同样，，也只想到了暴力，复杂度当然降不下来，然后又因为是异或，不是以前的加减，觉得线段树用不上，，于是

就放弃了。

分析：其实发现区间问题一般要用到线段树或者BIT，，，这道题就是，跟线段树不同的是，这道题是异或运算而不是加减。。

直接求偶数的异或比较麻烦，所以需要对异或进行一下分析，可以发现：

1.a^b^b=a;//所以整个区间所有数字的异或=出现次数奇数次的数异或

2.出现奇数次的数异或结果^出现偶数次的数的异或结果=所有出现过的数的异或结果

=>出现偶数次的异或=所有出现过的数异或^整个区间所有数字的异或；

前者用线段树+map维护

http://blog.csdn.net/baidu_35520981/article/details/52130388