啊哈！算法（第二章）C#实现

第 1 节 解密 QQ 号——队列

 

新学期开始了，小哈是小哼的新同桌（小哈是个小美女哦~），小哼向小哈询问 QQ 号，小哈当然不会直接告诉小哼啦，原因嘛你懂的。

所以小哈给了小哼一串加密过的数字，同时小哈也告诉了小哼解密规则。

规则是这样的：首先将第 1 个数删除，紧接着将第 2 个数放到这串数的末尾，再将第 3 个数删除并将第 4 个数放到这串数的末尾，再将第 5 个数删除……

直到剩下最后一个数，将最后一个数也删除。按照刚才删除的顺序，把这些删除的数连在一起就是小哈的 QQ 啦。

现在你来帮帮小哼吧。小哈给小哼加密过的一串数是“6 3 1 7 5 8 9 2 4”。

 

 internal struct queue
 {
     public int[] data;
     public int head;
     public int tail;
 }

 static void Main(string[] args)
 {
     queue q = new queue();
     q.data = new int[];
     q.head = ;
     q.tail = ;

     for (int i = ; i <= ; i++)
     {
         q.data[i] = Convert.ToInt32(Console.ReadLine());
         q.tail++;
     }

     while(q.head < q.tail)
     {
         Console.Write(q.data[q.head]);
         q.head++;

         q.data[q.tail] = q.data[q.head];
         q.head++;
         q.tail++;
     }
 }

解密的第一步是将第一个数删除，你可以想一下如何在数组中删除一个数呢。

最简单的方法是将所有后面的数都往前面挪动一位，将前面的数覆盖。

就好比我们在排队买票，最前面的人买好离开了，后面所有的人就需要全部向前面走一步，补上之前的空位，但是这样的做法很耗费时间。

 

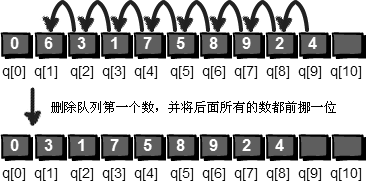
在这里，我将引入两个整型变量head 和tail。

head 用来记录队列的队首（即第一位），tail 用来记录队列的队尾（即最后一位）的下一个位置。

你可能会问：为什么tail 不直接记录队尾，却要记录队尾的下一个位置呢？

这是因为当队列中只剩下一个元素时，队首和队尾重合会带来一些麻烦。

我们这里规定队首和队尾重合时，队列为空。

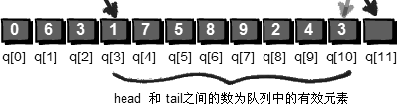
现在有9 个数，9 个数全部放入队列之后head=1;tail=10;此时head 和tail 之间的数就是目前队列中“有效”的数。

如果要删除一个数的话，就将head++就OK 了，这样仍然可以保持head 和tail 之间的数为目前队列中“有效”的数。

这样做虽然浪费了一个空间，却节省了大量的时间，这是非常划算的。

新增加一个数也很简单，把需要增加的数放到队尾即q[tail]之后再tail++就OK 啦。

我们来小结一下，在队首删除一个数的操作是head++;。

在队尾增加一个数（假设这个数是x）的操作是q[tail]=x;tail++;。

整个解密过程，请看下面这个霸气外漏的图。

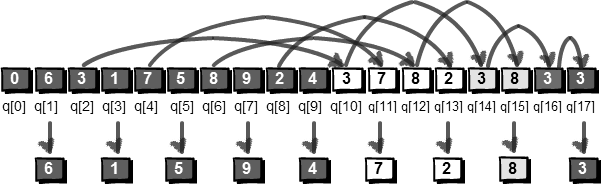
最后的输出就是6 1 5 9 4 7 2 8 3

 

队列是一种特殊的线性结构，它只允许在队列的首部（head）进行删除操作，这称为“出队”，而在队列的尾部（tail）进行插入操作，这称为“入队”。

当队列中没有元素时（即 head==tail），称为空队列。

在我们的日常生活中有很多情况都符合队列的特性。

比如我们之前提到过的买票，每个排队买票的窗口就是一个队列。

在这个队列当中，新来的人总是站在队列的最后面，来得越早的人越靠前，也就越早能买到票，就是先来的人先服务，我们称为“先进先出”（FirstIn First Out，FIFO）原则

---

 

第2 节 解密回文——栈

 

队列是先进先出，而栈相反，先进后出

拿书中的例子来讲，我们将1，2，3号球，放进竹筒里，效果应该是这样的

3

2

1

 

 

 

这个时要取出1号球，就要先将3，2依此取出后，才能够得到1

 

于是我们就可以利用栈来解决一个小小的问题，就是回文字符串

 

回文字符串就是指正读反读均相同的字符序列，如“席主席”、“记书记”、“aha”和“ahaha”均是回文

 

就拿xyzyx举例

 

先从字符串中间开始，我们让前半部分，放入栈中

x

y

 

 

然后越过中心点z，对后半部分的字符串进行判断，利用栈的特点，第一个出来的是y，而刚好中心点后的字符也是y，依此类推进行判断

 static void PalindromeString()
 {
     Write("请输入一串字符：");
     string str = ReadLine();
     char[] cstr = str.ToCharArray();

     //设置栈
     char[] stack = new char[];

     //得到字符串的长度
     int len = str.Length;
     //得到字符串中间点
     int mid = len/;
     //初始化栈顶
     int top = ;

     //将字符串前半段入栈
     for (int i = ; i < mid; i++)
     {
         stack[top] = cstr[i];
         top++;
     }

     //如果字符长度是偶数，就不需要+1到中间点
     int next = (len%) ==  ? mid : (mid+);

     //接着往下判断
     for (int i = next; i < len; i++)
     {
         //减一原因就是，数组长度-1位
         --top;
         //判断是否回文，利用栈的特点先进后出
         if(str[i] != stack[top]) break;
     }

     WriteLine(top==?"yes":"no");
 }

栈还可以用来进行验证括号的匹配。比如输入一行只包含“()[]{}”的字符串，请判断
形如“([{}()])”或者“{()[]{}}”的是否可以正确匹配。显然上面两个例子都是可以正确匹
配的。“([)]”是不能匹配的。有兴趣的同学可以自己动手来试一试。

代码参考来源此处：https://www.jianshu.com/p/5bf5aecc9cd5

static void Main(string[] args)
{
    //左边括号
    string left= "{([<";
    //右边括号
    string right = "})]>";

    bool flag = false;

    Write("请输入一组括号组合(),[],{},<>：");
    char[] cstr = ReadLine().ToCharArray();

    //初始化栈
    Stack stack = new Stack(cstr.Length*);
    for (int i = ; i < cstr.Length; i++)
    {
        int indexleft = -, indexright = -;
        indexleft = left.IndexOf(cstr[i]);
        indexright = right.IndexOf(cstr[i]);

        if(indexleft >= )
        {
            stack.push(cstr[i]);
        }
        else if(indexright >= )
        {
            if(!stack.isEmpty() && (stack.peek() == left.ToCharArray()[indexright]))
            {
                stack.pop();
            }
            else
            {
                flag = true;
                break;
            }
        }
    }

    if(flag) {
        WriteLine("no");
        return;
    };
    //栈清空，表示匹配完毕
    WriteLine(stack.isEmpty()?"yes":"no");
}

class Stack
{
    public char[] values { get => stack;}
    private char[] stack;
    private int top = ;
    public Stack(int max)
    {
        stack = new char[max];
    }
    public void push(char c) => stack[top++] = c;
    public char peek()
    {
        return stack[top-];
    }
    public void pop()
    {
        top--;
        stack[top] = '\0';
    }
    public bool isEmpty()
    {
        int i = ;
        foreach (var item in stack)
        {
            if(item == '\0')
                i++;
        }
        return i == stack.Length ? true : false;
    }
}