python实现二叉树的遍历以及基本操作

主要内容：

1. 二叉树遍历（先序、中序、后序、宽度优先遍历）的迭代实现和递归实现；

2. 二叉树的深度，二叉树到叶子节点的所有路径；

首先，先定义二叉树类（python3），代码如下：

class TreeNode:
     def __init__(self, x):
         self.val = x
         self.left = None
         self.right = None

目录

• 1.1 先序遍历：
• 1.2 中序遍历
• 1.3 后序遍历
• 1.4 层次遍历

二叉树的遍历分深度优先遍历（DFS）和宽度优先遍历（BFS）。其中深度优先遍历又分为先序遍历，中序遍历，后序遍历。因为二叉树是递归类数据结构，因此大部分关于二叉树的操作都可以通过递归实现。下面将介绍二叉树几种遍历的实现代码以及思路。

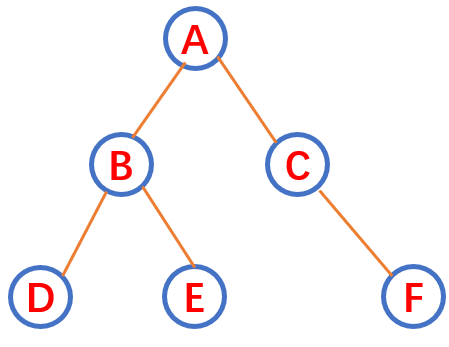
1.1 先序遍历：

遍历顺序：根节点——左子节点——右子节点（A-B-D-E-C-F）。

递归实现：

def preorder(root):
    if not root:
        return
    print(root.val)
    preorder(root.left)
    preorder(root.right)

迭代实现：

def preorder(root):
    stack = [root]
    while stack:
        s = stack.pop()
        if s:
            print(s.val)
            stack.append(s.right)
            stack.append(s.left)

1.2 中序遍历

遍历顺序：左子节点——根节点——右子节点（D-B-E-A-C-F）

递归实现：

def inorder(root):
    if not root:
        return
    inorder(root.left)
    print(root.val)
    inorder(root.right)

迭代实现：

def inorder(root):
    stack = []
    while stack or root:
        while root:
            stack.append(root)
            root = root.left
        root = stack.pop()
        print(root.val)
        root = root.right

1.3 后序遍历

遍历顺序：左子节点——右子节点——根节点（D-E-B-F-C-A）

递归实现：

def postorder(root):
    if not root:
        return
    postorder(root.left)
    postorder(root.right)
    print(root.val)

迭代实现：

def postorder(root):
    stack = []
    while stack or root:
        while root:                 # 下行循环，直到找到第一个叶子节点

            stack.append(root)
            if root.left:           # 能左就左，不能左就右

                root = root.left
            else:
                root = root.right
        s = stack.pop()
        print(s.val)
        #如果当前节点是上一节点的左子节点，则遍历右子节点

        if stack and s == stack[-1].left: 

            root = stack[-1].right
        else:
            root = None

1.4 层次遍历

遍历顺序：一层一层的遍历（A-B-C-D-E-F）

迭代实现：

def BFS(root):
    queue = [root]
    while queue:
        n = len(queue)
        for i in range(n):
            q = queue.pop(0)
            if q:
                print(q.val)
                queue.append(q.left if q.left else None)
                queue.append(q.right if q.right else None)

内容2：基本操作

2.1 二叉树的最大深度

基本思路就是递归，当前树的最大深度等于（1+max(左子树最大深度，右子树最大深度)）。代码如下：

def maxDepth(root):

    if not root:
        return 0
    return 1+max(maxDepth(root.left),maxDepth(root.right))

2.2 二叉树的最小深度

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。可以通过递归求左右节点的最小深度的较小值，也可以层序遍历找到第一个叶子节点所在的层数。

递归方法：

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if not root.left and not root.right:
            return 1
        if not root.right:
            return 1+self.minDepth(root.left)
        if not root.left:
            return 1+self.minDepth(root.right)
        return 1+min(self.minDepth(root.left),self.minDepth(root.right))

迭代方法：

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root: return 0
        ans,count = [root],1
        while ans:
            n = len(ans)
            for i in range(n):
                r = ans.pop(0)
                if r:
                    if not r.left and not r.right:
                        return count
                    ans.append(r.left if r.left else [])
                    ans.append(r.right if r.right else [])
            count+=1

2.3 二叉树的所有路径

根节点到叶子节点的所有路径。

def traverse(node):
    if not node.left and not node.right:
        return [str(node.val)]
    left, right = [], []
    if node.left:
        left = [str(node.val) + x for x in traverse(node.left)]
    if node.right:
        right = [str(node.val) + x for x in traverse(node.right)]

    return left + right