hud 1465、2049、2045 （递推）[含简单C(n,m) n!的写法]

C - 不容易系列之一

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status Practice HDU 1465

Appoint description: 
System Crawler  (2016-03-11)

Description

大家常常感慨，要做好一件事情真的不容易，确实，失败比成功容易多了！ 
做好“一件”事情尚且不易，若想永远成功而总从不失败，那更是难上加难了，就像花钱总是比挣钱容易的道理一样。 
话虽这样说，我还是要告诉大家，要想失败到一定程度也是不容易的。比如，我高中的时候，就有一个神奇的女生，在英语考试的时候，竟然把40个单项选择题全部做错了！大家都学过概率论，应该知道出现这种情况的概率，所以至今我都觉得这是一件神奇的事情。如果套用一句经典的评语，我们可以这样总结：一个人做错一道选择题并不难，难的是全部做错，一个不对。

不幸的是，这种小概率事件又发生了，而且就在我们身边： 
事情是这样的――HDU有个网名叫做8006的男性同学，结交网友无数，最近该同学玩起了浪漫，同时给n个网友每人写了一封信，这都没什么，要命的是，他竟然把所有的信都装错了信封！注意了，是全部装错哟！

现在的问题是：请大家帮可怜的8006同学计算一下，一共有多少种可能的错误方式呢？

 

Input

输入数据包含多个多个测试实例，每个测试实例占用一行，每行包含一个正整数n（1<n<=20），n表示8006的网友的人数。

 

Output

对于每行输入请输出可能的错误方式的数量，每个实例的输出占用一行。

 

Sample Input

2
3

 

Sample Output

1
2

 

典型的全错排.

我的想法: f[n] 表示 n的全错排, 显然 f[1] = 0, f[2] = 1, n的全错排等于n的全排列减去含1~n个正确的,

n个正确, 共有 1 种

n-1个正确, 有 C(n,1)*f[1]种, 实际上这个是0 因为f[1]=0

n-2个正确, 有 C(n,2)*f[2]种,

...

1 个 正确, 有C(n,n-1)*f[n-1]种

这些都加起来, 再用n!减即可

#include<stdio.h>
#include<iostream>
using namespace std;

__int64 nn (int x)
{
    if(x == )return ;
    return x * nn(x-);
}

__int64 Cmn(int m, int n)
{
    if(m < n || n < ) return ;
    if(m == n || n == ) return ;
    return (Cmn(m-, n-) + Cmn(m-, n));
}

int main()
{
    __int64 a, f[],sum;
    f[] = ;
    f[] = ;
    //f[3] = 2;
    //f[4] = 9;
    for(int i = ; i < ; i++)
    {
        sum = ;
        for(int j = ; j < i-; j++)
            sum += Cmn(i,j)*f[i-j];
        sum += ;
        f[i] = nn(i)-sum;
    }
    while(cin>>a)
    {
        cout<<f[a]<<endl;
    }
    return ;
}

然而大家都是这么做的, 理解一下就是, n的全错排等于两种情况的加和, 前n-1的所有排列方式,  其中 n-1 这个有排错了和没排错两种: 如果派错了 即前n-1的是全错排,第n个和前面任意一个交换, 这样就有n-1*f[n-1]种, 如果n-1没排错, 那是前n-2的全错排,第n个和n-1个交换.

#include<stdio.h>
#include<iostream>
using namespace std;

int main()
{
    __int64 a, f[],sum;
    f[] = ;
    f[] = ;
    for(int i = ; i < ; i++)
    {
        f[i] = (i-)*(f[i-] + f[i-]);
    }
    while(cin>>a)
    {
        cout<<f[a]<<endl;
    }
    return ;
}

这种分n-1和n-2来讨论的思想, 2045题也用到

F - 不容易系列之(4)――考新郎

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status Practice HDU 2049

Appoint description: 
System Crawler  (2016-03-09)

Description

国庆期间,省城HZ刚刚举行了一场盛大的集体婚礼,为了使婚礼进行的丰富一些,司仪临时想出了有一个有意思的节目,叫做"考新郎",具体的操作是这样的: 

首先,给每位新娘打扮得几乎一模一样,并盖上大大的红盖头随机坐成一排; 
然后,让各位新郎寻找自己的新娘.每人只准找一个,并且不允许多人找一个. 
最后,揭开盖头,如果找错了对象就要当众跪搓衣板...

看来做新郎也不是容易的事情...

假设一共有N对新婚夫妇,其中有M个新郎找错了新娘,求发生这种情况一共有多少种可能. 

 

Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C行数据，每行包含两个整数N和M(1<M<=N<=20)。 

 

Output

对于每个测试实例，请输出一共有多少种发生这种情况的可能，每个实例的输出占一行。 

 

Sample Input

2
2 2
3 2

 

Sample Output

1
3

这题就是上面那个题加一个简单的Cnm的公式

#include<stdio.h>
#include<iostream>

using namespace std;

__int64 Cnm(int n, int m)
{
    if(m == n || m == ) return ;
    return (Cnm(n-, m-) + Cnm(n-, m));
}

int main()
{
    __int64 a, f[],sum;
    f[] = ;
    f[] = ;
    for(int i = ; i < ; i++)
    {
        f[i] = (i-)*(f[i-] + f[i-]);
    }
    int T;cin>>T;
    while(T--)
    {
        int n,m;
        while(cin>>n>>m)
        {
            cout<<f[m]*Cnm(n,m)<<endl;
        }
    }

    return ;
}

但是还可以再优化一下, 针对Cmn用的是递归, 可以改成循环并且打表

先复习一下排列组合公式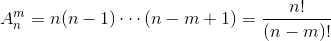         

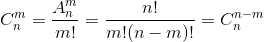
#include<stdio.h>
#include<iostream>

using namespace std;

int main()
{
    __int64 a, f[],sum, N[];
    f[] = ;
    f[] = ;
    N[] = ;
    N[] = ;
    N[] = ;
    for(int i = ; i < ; i++)
    {
        f[i] = (i-)*(f[i-] + f[i-]);
        N[i] = N[i-]*i;
    }
    int T;cin>>T;
    while(T--)
    {
        int n,m;
        while(cin>>n>>m)
        {
            cout<< N[n]/(N[m]*N[n-m]) * f[m]<<endl;
            //注意这里不能写成 f[m]  * N[n]/(N[m]*N[n-m]) 会WA
            //原因可能是前面f[m]  * N[n] 乘爆了
        }
    }

    return ;
}

E - 不容易系列之(3)―― LELE的RPG难题

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status Practice HDU 2045

Appoint description: 
System Crawler  (2016-03-10)

Description

人称“AC女之杀手”的超级偶像LELE最近忽然玩起了深沉，这可急坏了众多“Cole”（LELE的粉丝,即"可乐"）,经过多方打探，某资深Cole终于知道了原因，原来，LELE最近研究起了著名的RPG难题:

有排成一行的ｎ个方格，用红(Red)、粉(Pink)、绿(Green)三色涂每个格子，每格涂一色，要求任何相邻的方格不能同色，且首尾两格也不同色．求全部的满足要求的涂法.

以上就是著名的RPG难题.

如果你是Cole,我想你一定会想尽办法帮助LELE解决这个问题的;如果不是,看在众多漂亮的痛不欲生的Cole女的面子上,你也不会袖手旁观吧?

 

Input

输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成，(0<n<=50)。 

 

Output

对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。 

 

Sample Input

1
2

 

Sample Output

3
6

直接上代码

#include<stdio.h>
#include<iostream>
using namespace std;

__int64 f[M];

int main()
{
    int n;
    f[] = ;
    f[] = ;
    f[] = ;
    for(int i = ; i<; i++)
    {
        f[i] = f[i-] +f[i-]*;
    }
    while(cin>>n)
    {
        cout<<f[n]<<endl;
    }
    return ;
}