洛谷P2668斗地主（搜索）noip2015

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

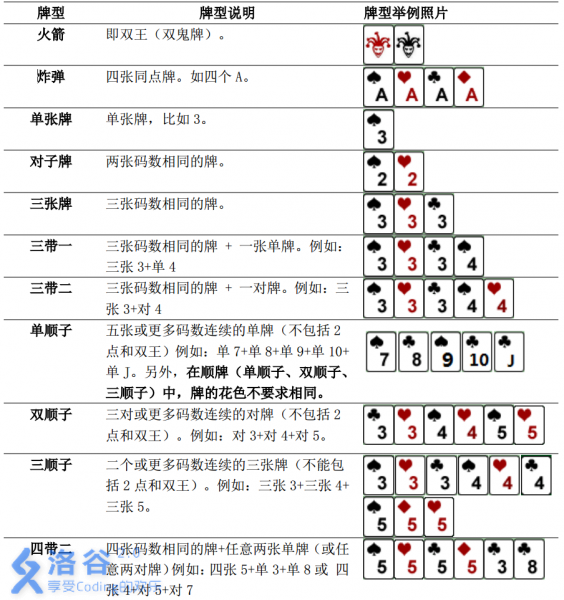
输入输出格式

输入格式：

第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。

输出格式：

共T行，每行一个整数，表示打光第i手牌的最少次数。

输入输出样例

输入样例#1：

输出样例#1：

输入样例#2：

输出样例#2：

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

对于不同的测试点，我们约定手牌组数T与张数n的规模如下：

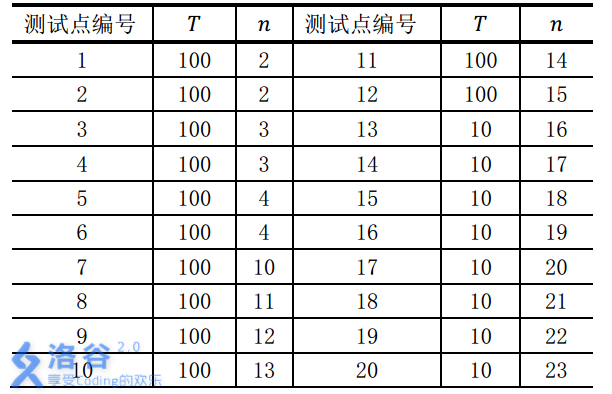
数据保证：所有的手牌都是随机生成的。

#include<iostream>

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

int x[],y[],z[],k[],num[];

int T,cnt,flag,n;

bool cmp(int a,int b)

{

    return a>b;

}

int main()

{

    scanf("%d%d",&T,&n);

    while(T--)

    {

        flag=,cnt=;

        memset(z,,sizeof z);

        memset(x,,sizeof x);

        memset(num,,sizeof num);

        if(n>) return ;

        for(int i=;i<=n;i++)

        {

            scanf("%d%d",&x[i],&y[i]);

            num[x[i]]++;

        }

        for(int i=;i<=;i++)

        {

            if(num[i]!=)

              z[++cnt]=num[i];

        }

        sort(z+,z+n+,cmp);

        if(z[]==)

        {

            cout<<n<<endl;

            continue;

        }

        if(z[]==n)

        {

            cout<<""<<endl;

            continue;

        }

        if(z[]==)

        {

            cout<<""<<endl;

            continue;

        }

        if((z[]==&&z[]==))

        {

            cout<<""<<endl;

            continue;

        }

        if((z[]==&&z[]==&&z[]==))

        {

            cout<<""<<endl;

            continue;

        }

        if(n==&&z[]==)

        {

            cout<<""<<endl;

            continue;

        }

    }

    return ;

}

最无脑的暴力30分...

dfs+贪心

#include <iostream>

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <cmath>

#include <algorithm>

using namespace std;

int T,n,num[],ans,p[];//num代表第i种牌有几个，p代表剩下i张的牌有几种

void rest(int x,int u)

{

    int temp=u;

    bool flag=false;

    if (num[]&&num[]) flag=true;//是否有王炸

    memset(p,,sizeof(p));

    for (int i=; i<=; i++) p[num[i]]++;

    if (p[]!=)   //四牌特判

    {

        temp+=p[];

        if (p[]>=p[]*) p[]-=p[]*;//对子够用,四带二

        else   //对子不够，单张上，四帯一

        {

            p[]-=p[]/;

            p[]=p[]%;

            if (p[]>=p[]*) p[]-=p[]*;

            else p[]=p[]%;

        }

    }

    if (p[]!=)   //同炸弹

    {

        temp+=p[];

        if (p[]>=p[]) p[]-=p[];

        else

        {

            p[]-=p[];

            p[]=;

            if (p[]>=p[]) p[]-=p[];

            else p[]=;

        }

    }

    if (p[]!=) temp+=p[];

    if (p[]>=&&flag) temp+=p[]-;

    else temp+=p[];//如果单张剩余2张以上，又存在王炸，那么就把两张单张当成王炸出掉。

    ans=min(ans,temp);

    return;

}

void dfs(int x,int u)//剩余x张牌,已经用了u步

{

    if (u>=ans) return;//剪枝

    if (x==)

    {

        ans=min(u,ans);

        return;

    }

    int start=,end=;

    //------单顺-------------

    if (x>=)

    {

        //每个搜顺子开头都有的小剪枝

        for (int i=; i<=; i++)   //注意只能搜到A

        {

            if (num[i-]==) start=i;//上一张不够牌，所以这张开始做顺头

            if (num[i]!=) end=i;//这张是够的，所以顺尾后移

            if (end-start+>=)   //如果牌够了

            {

                for (int k=; k<=end-start+; k++)

                {

                    //要记得start也可以后移，不然一直只能以start开始顺子，直到start改变

                    start+=k-;//我就是这里写错调了好久。。。

                    for (int j=start; j<=end; j++) num[j]--;

                    dfs(x-(end-start+),u+);

                    for (int j=start; j<=end; j++) num[j]++;

                    start-=k-;

                }

            }

        }

    }

    start=;

    end=;

    //------双顺-------------

    if (x>=)   //全部同单顺

    {

        for (int i=; i<=; i++)

        {

            if (num[i-]<=) start=i;

            if (num[i]>) end=i;

            if (end-start+>=)

            {

                for (int k=; k<=end-start+; k++)

                {

                    start+=k-;

                    for (int j=start; j<=end; j++) num[j]-=;

                    dfs(x-(end-start+)*,u+);

                    for (int j=start; j<=end; j++) num[j]+=;

                    start-=k-;

                }

            }

        }

    }

    start=;

    end=;

    //------san shun-------------

    if (x>=)

    {

        for (int i=; i<=; i++)

        {

            if (num[i-]<=) start=i;

            if (num[i]>) end=i;

            if (end-start+>=)

            {

                for (int k=; k<=end-start+; k++)

                {

                    start+=k-;

                    for (int j=start; j<=end; j++) num[j]-=;

                    dfs(x-(end-start+)*,u+);

                    for (int j=start; j<=end; j++) num[j]+=;

                    start-=k-;

                }

            }

        }

    }

    rest(x,u);//贪心

    return;

}

int main()

{

    scanf("%d%d",&T,&n);

    for (int qwe=; qwe<=T; qwe++)

    {

        memset(num,,sizeof(num));

        ans=0x3f3f3f3f;//重要的初始化

        for (int i=; i<=n; i++)

        {

            int a,b;

            scanf("%d%d",&a,&b);//花色没用，仅仅在大小王上有用

            if (a==)

            {

                if (b==) num[]++;    //大小王视为单张。。。

                if (b==) num[]++;

            }

            else

            {

                if (a==) num[]++;

                else if (a==) num[]++;

                else num[a-]++;//3->1 4->2 ..... K->11 A->12 2->13 这里是方便搜顺子

            }

        }

        dfs(n,);

        printf("%d\n",ans);

    }

    return ;

}

//我真的好笨...... 就不想写dfs，就是不对! 唉......

#include<iostream>

#include<cstdio>

#include<cstring>

#define maxn 50

using namespace std;

int poker_cnt[maxn],poker_now[maxn];

int x,y,t,n,ans,cnt,num,pos,start,flag,flag_2,c;

inline int init()

{

    int x=,f=;char c=getchar();

    while(c>''||c<''){if(c=='-')f=-;c=getchar();}

    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}

    return x*f;

}

void work1()

{

    for(int i=;i<=;i++)

    {

        if(poker_cnt[i+]&&poker_cnt[i])

        {

            cnt=;start=i;pos=i;

            while(poker_cnt[pos]&&pos<=){cnt++;pos++;}

            if(cnt>=)

            {

                for(int j=start;j<=start+cnt-;j++)poker_cnt[j]--;

                n-=cnt;ans++;

            }

        }

    }

}

void work2()

{

    flag=;

    for(int i=;i<=;i++)

    {

        flag_2=;int pd1=,pd2=,pos2=;

        if(poker_cnt[i]==)

        {

          for(int j=;j<=;j++) for(int k=;k<=;k++)

          {

               if(poker_cnt[j]>=&&poker_cnt[k]>=&&k!=j&&!flag_2)

               {

                   flag=;

                   if(poker_cnt[j]==) pd1=k;if(poker_cnt[k]==) pd1=j;

                   for(int l=;l<=;l++)

                  if(poker_cnt[l]==&&l!=pd1) pd2=,pos2=l;

                  if(!pd2)poker_cnt[k]--,poker_cnt[j]--,poker_cnt[i]-=;

                  else poker_cnt[pd1]--,poker_cnt[pos2]--,poker_cnt[i]-=;

                  n-=;ans++;flag_2=;

               }

               if(poker_cnt[j]==&&poker_cnt[k]==&&k!=j&&!flag_2)

               {

                     flag=;

                  poker_cnt[k]-=;poker_cnt[j]-=;poker_cnt[i]-=;

                  n-=;ans++;flag_2=;

               }

          }

          if(!flag) poker_cnt[i]-=,n-=,ans++;

        }

    }

}

void work3()

{

    for(int i=;i<=;i++)

    {

        if(poker_cnt[i]==&&poker_cnt[i+]==)

        {

            start=i;pos=i;cnt=;

            while(poker_cnt[pos]==){cnt++;pos++;}

            if(cnt>=)

            {

                n-=cnt*;ans++;

                for(int i=start;i<=cnt+start-;i++) poker_cnt[i]-=;

            }

        }

        if(poker_cnt[i]==&&poker_cnt[i+]==)

        {

            start=i;pos=i;cnt=;

            while(poker_cnt[pos]==){cnt++;pos++;}

            if(cnt>=)

            {

                n-=cnt*;ans++;

                for(int i=start;i<=cnt+start-;i++) poker_cnt[i]-=;

            }

        }

    }

}

void work4()

{

    flag=;

    for(int i=;i<=;i++)

    {

        flag_2=;

        if(poker_cnt[i]==)

        {

            for(int j=;j<=;j++)

            {

                if(poker_cnt[j]==&&!flag_2)

                {

                    flag=;

                    poker_cnt[j]--;poker_cnt[i]-=;

                    n-=;ans++;flag_2=;

                }

            }

            if(!flag) poker_cnt[i]-=,n-=,ans++;

        }

    }

}

inline void work5()

{

    for(int i=;i<=;i++)

    {

       if(poker_cnt[i])

       {

            n-=poker_cnt[i];ans++;

          poker_cnt[i]=;

       }

    }

}

int main()

{

    freopen("landlords8.in","r",stdin);

//    freopen("landlords.out","w",stdout);

    t=init();n=init();c=n;int d=n;

    while(t--)

    {

        c=d;n=d;

        flag=;ans=;memset(poker_cnt,,sizeof poker_cnt);

        pos=;start=;memset(poker_now,,sizeof poker_now);

        while(c--){x=init();y=init();poker_cnt[x]++;}

        poker_cnt[]=poker_cnt[];poker_cnt[]=poker_cnt[];poker_cnt[]=poker_cnt[];

        for(int i=;i<=;i++) poker_cnt[i-]=poker_cnt[i];poker_cnt[]=;

        poker_cnt[]=;poker_cnt[]=;

        if(n>=) work1();//顺子

        if(n>=) work2();//四张牌与四带二

        if(n>=) work3();//连对，三连对

        if(n>=) work4();//三带一

        if(n) work5();//单 对牌

        if(n==) printf("%d\n",ans);

    }

}

2017 5.20 35分