Dijkstra再理解+最短路计数

众所周知，Dijkstra算法是跑单源最短路的一种优秀算法，不过他的缺点在于难以处理负权边。

但是由于在今年的NOI赛场上SPFA那啥了（嗯就是那啥了），所以我们还是好好研究一下Dij的原理和它的优化吧。

（前面那篇写的太简陋了）

1.Dijkstra算法的原理

首先，我们先假设整个图已经被建完而且所有边权全部为正。使用dis[i]表示从原点s到i点的最短距离。之后我们从选取的原点s开始，进行到汇点t的最短路搜寻。s一开始就会连向几个顶点，它所能到达的顶点的距离我们更新一

下，而不能到达的顶点的距离就先设为INF。之后，我们在这个点所能到达的所有点之中，找出一个dis最小的点，那么此时，到这个点的最短路径就已经被确定了。

这是为什么呢？因为图中所有边权全部为正，而当前点（u）的dis已经是最小的了，从其他点（v）再到这个点，所经过的距离必然大于dis[u]，也就是肯定不是到达u点的最短路。

因此这样我们就可以不断地确定一些点，之后再从确定的点集出发，去确定更多的点，这样就可以找到到汇点t的最短路径长度了。

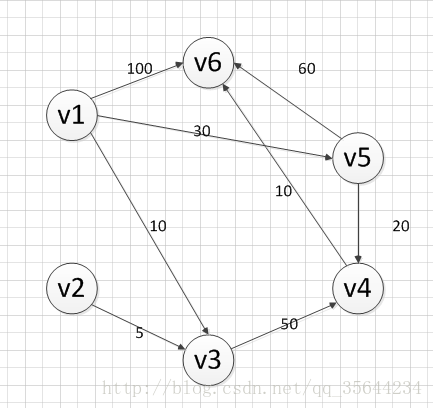
（我偷了别人的图和文章来演示如何求从顶点v1到其他各个顶点的最短路径）

首先第一步，我们先声明一个dis数组，该数组初始化的值为： 

我们的顶点集T的初始化为：T={v1}

既然是求 v1顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后，dis[2]（下标从0开始）的值就已经从“估计值”变为了“确定值”，即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。 
为什么呢？因为目前离 v1顶点最近的是 v3顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.

OK，既然确定了一个顶点的最短路径，下面我们就要根据这个新入的顶点V3会有出度，发现以v3 为弧尾的有： < v3,v4 >,那么我们看看路径：v1–v3–v4的长度是否比v1–v4短，其实这个已经是很明显的了，因为dis[3]代表的就是v1–v4的长度为无穷大，而v1–v3–v4的长度为：10+50=60，所以更新dis[3]的值,得到如下结果： 

因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3]，通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想：通过“边”来松弛v1顶点到其余各个顶点的路程。

然后，我们又从除dis[2]和dis[0]外的其他值中寻找最小值，发现dis[4]的值最小，通过之前是解释的原理，可以知道v1到v5的最短距离就是dis[4]的值，然后，我们把v5加入到集合T中，然后，考虑v5的出度是否会影响我们的数组dis的值，v5有两条出度：< v5,v4>和 < v5,v6>,然后我们发现：v1–v5–v4的长度为：50，而dis[3]的值为60，所以我们要更新dis[3]的值.另外，v1-v5-v6的长度为：90，而dis[5]为100，所以我们需要更新dis[5]的值。更新后的dis数组如下图： 

然后，继续从dis中选择未确定的顶点的值中选择一个最小的值，发现dis[3]的值是最小的，所以把v4加入到集合T中，此时集合T={v1,v3,v5,v4},然后，考虑v4的出度是否会影响我们的数组dis的值，v4有一条出度：< v4,v6>,然后我们发现：v1–v5–v4–v6的长度为：60，而dis[5]的值为90，所以我们要更新dis[5]的值，更新后的dis数组如下图： 

然后，我们使用同样原理，分别确定了v6和v2的最短路径，最后dis的数组的值如下： 

那么原理我们就说完了。

2.Dijkstra堆优化

Dijkstra的功能虽然强大，不过其时间复杂度比较大，对于n个点，每次最坏要枚举n次，时间复杂度是O（n^2）的。

这个复杂度有点大，我们考虑如何来优化呢？

首先，Dijkstra是基于贪心的，他每次都是找当前dis值最小的那一个点来继续更新。这样的话，每次的枚举就显得无用，我们直接维护当前最小值就可以了！所以优化就是使用set（小根堆）维护最小值，之后每次在贪心的时候取堆首元素，再更新堆首元素所能走到的点。每次更新的时候，把原来点存储的信息从set里面删掉，再压一个新的进去就可以了。时间复杂度被优化为O（nlogn）。

代码看下面的例题吧。

3.最短路计数

洛谷上的这道题比较简单，因为是无权图（其实有权也一样）。

非常easy的操作，正常跑一遍Dijkstra的堆优化，在每次松弛操作的时候，如果dis[u] > dis[v] + 1,那么到达u的最短路个数应该和到达v是一样的。如果dis[u] = dis[v] + 1,那么到达v的最短路个数应该加上到达u的最短路个数。

因为所有边的边权都是1，所以如果dis[u] = dis[v]+1，那么肯定从u经过的最短路，在v上经过的时候也是最短路。

这样就可以做了，注意取个模。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<set>
#include<cstdlib>
#include<cctype>
#include<queue>
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')

using namespace std;
typedef long long ll;
const int M = ;
const int mod = ;

int read()
{
    int ans = ,op = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-') op = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '')
    {
        ans *= ;
        ans += ch - '';
        ch = getchar();
    }
    return ans * op;
}
#define pr pair<int,int>
#define mp make_pair
set <pr> q;
set <pr> :: iterator it;
int n,m,ecnt,head[M],x,y,dis[M],num[M];
bool vis[M];
struct node
{
    int next,to;
}e[M<<];

void add(int x,int y)
{
    e[++ecnt].next = head[x];
    e[ecnt].to = y;
    head[x] = ecnt;
}
void dij(int s)
{
    rep(i,,n) dis[i] = ;
    dis[s] = ,num[s] = ;
    q.insert(mp(dis[s],s));
    while(!q.empty())
    {
        pr k = *(q.begin());
        q.erase(q.begin());
        vis[k.second] = ;
        for(int i = head[k.second];i;i = e[i].next)
        {
            if(dis[e[i].to] > dis[k.second] + )
            {
                it = q.find(mp(dis[e[i].to],e[i].to));
                if(it != q.end()) q.erase(it);
                dis[e[i].to] = dis[k.second] + ;
                num[e[i].to] = num[k.second];
                q.insert(mp(dis[e[i].to],e[i].to));
            }
            else if(dis[e[i].to] == dis[k.second] + )
            {
                num[e[i].to] += num[k.second];
                num[e[i].to] %= mod;
            }
        }
    }
}
int main()
{
    n = read(), m = read();
    rep(i,,m) x = read(), y = read(), add(x,y), add(y,x);
    dij();
    rep(i,,n) printf("%d\n",num[i]);
    return ;
}