HDU 4923 Room and Moor(瞎搞题)

瞎搞题啊。找出1 1 0 0这样的序列，然后存起来，这样的情况下最好的选择是1的个数除以这段的总和。

然后从前向后扫一遍。变扫边进行合并。每次合并。合并的是他的前驱。这样到最后从t-1找出的那条链就是最后满足条件的数的大小。

Room and Moor

Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)

Total Submission(s): 307    Accepted Submission(s): 90

Problem Description

PM Room defines a sequence A = {A₁, A₂,..., A_N}, each of which is either 0 or 1. In order to beat him, programmer Moor has to construct another sequence B = {B₁, B₂,... , B_N} of the same length,
which satisfies that:

 

Input

The input consists of multiple test cases. The number of test cases T(T<=100) occurs in the first line of input.



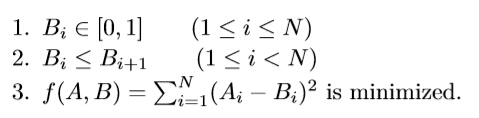
For each test case:

The first line contains a single integer N (1<=N<=100000), which denotes the length of A and B.

The second line consists of N integers, where the ith denotes A_i.

 

Output

Output the minimal f (A, B) when B is optimal and round it to 6 decimals.

 

Sample Input

4
9
1 1 1 1 1 0 0 1 1
9
1 1 0 0 1 1 1 1 1
4
0 0 1 1
4
0 1 1 1

 

Sample Output

1.428571
1.000000
0.000000
0.000000

 

Source

field=problem&key=2014%20Multi-University%20Training%20Contest%206&source=1&searchmode=source" style="color:rgb(26,92,200); text-decoration:none">2014 Multi-University Training Contest 6

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
#define LL __int64
///#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?

0:x)

using namespace std;

const int maxn = 1000010;
int num[maxn];
int sum[maxn][2];
int pre[maxn];
double x[maxn];

int main()
{
    int T;
    cin >>T;
    while(T--)
    {
        int n;
        scanf("%d",&n);
        for(int i = 0; i < n; i++) scanf("%d",&num[i]);
        int t = 0;
        int cnt1 = 0;
        int cnt2 = 0;
        if(!num[0]) cnt1 = 1;
        if(num[0]) cnt2 = 1;
        for(int i = 1; i < n; i++)
        {
            if(num[i] > num[i-1])
            {
                sum[t][0] = cnt1;
                sum[t++][1] = cnt2;
                cnt1 = cnt2 = 0;
                if(!num[i]) cnt1++;
                if(num[i]) cnt2++;
                continue;
            }
            if(!num[i]) cnt1++;
            if(num[i]) cnt2++;
        }
        sum[t][0] = cnt1;
        sum[t][1] = cnt2;
        t++;
        for(int i = 0 ; i < t; i++) x[i] = (1.0*sum[i][1]/((sum[i][0]+sum[i][1])*1.0));
        pre[0] = -1;
        for(int i = 1; i < t; i++)
        {
            if(x[i] < x[i-1])
            {
                sum[i][0] += sum[i-1][0];
                sum[i][1] += sum[i-1][1];
                x[i] = 1.0*sum[i][1]/(sum[i][1]+sum[i][0])*1.0;
                pre[i] = pre[i-1];
                int p = pre[i];
                while(p != -1)
                {
                    if(x[i] < x[p])
                    {
                        sum[i][0] += sum[p][0];
                        sum[i][1] += sum[p][1];
                        x[i] = 1.0*sum[i][1]/(sum[i][0]+sum[i][1])*1.0;
                        pre[i] = pre[p];
                        p = pre[p];
                        continue;
                    }
                    break;
                }
                continue;
            }
            pre[i] = i-1;
        }
        int p = pre[t-1];
        double ans =0;
        ans += sum[t-1][0]*pow(x[t-1], 2)+sum[t-1][1]*pow(x[t-1]-1, 2);
        while(p != -1)
        {
            ans += sum[p][0]*pow(x[p], 2)+sum[p][1]*pow(x[p]-1, 2);
            p = pre[p];
        }
        printf("%.6lf\n",ans);
    }
    return 0;
}