2017zstu新生赛
1.b^3 - a^3 = c（zy）
zy说要卡nlogn的，然而他实际给的组数只有100组，然后因为在windows下随机的，所以给出的 c <= 100000。然后只要胆子大。。。。
通过打表发现，x^3-(x-1)^3 <= 1e9, x的最大值是18258
然后我们用一个数组去记录 2^3-1^3, 3^3-2^3, 4^3-3^3, ...., 18258^3-18257^3
对于c, 用尺取去判断就好了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int UP = + ;
vector<ll> ss;
int c; int main () {
for (ll i=; i<UP; ++i) {
ss.emplace_back(i*i*i-(i-)*(i-)*(i-));
}
freopen("1.in","r",stdin);
freopen("11.out","w",stdout);
while (~ scanf("%d", &c)) {
ll sum = ;
deque<int> q;
bool flag = false;
for (int i=; i<UP; ++i) {
q.push_back(i);
sum += ss[i];
while (!q.empty() && sum>c) {
sum -= ss[q.front()];
q.pop_front();
}
if (sum==c) {
flag = true;
printf ("%d %d\n", q.front()+, q.back()+);
break;
}
}
if (!flag) puts("-1");
}
return ;
}
2.cs的禁断魔法（zy）
主席树 + 二分，然后感觉是所有题里写起来最费劲的
deep是点在树上的深度，maxdeep(i) : 表示在i这棵子树里，会出现的最大deep
把所有点按照(deep, val)去sort，然后按照deep从小到大去建主席树。
建主席树就是按照dfs序插入到线段树里，然后区间维护最小值。
然后对于每次询问 x c, 就二分深度，然后用主席树check就好了
总体复杂度：O(nlogn + Qloglog)
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int M = 1e5+;
const int logn = ;
const int nill = ;
typedef pair<int,int> pii;
int deep[M], maxndeep[M];
pii a[M];
int val[M];
vector<int> g[M];
int tin[M], tout[M], tim;
int n, Q; void dfs (int u) {
tin[u] = ++tim;
maxndeep[u] = deep[u];
for (int i=; i<g[u].size(); ++i) {
int v = g[u][i];
deep[v] = deep[u]+;
a[v].first = a[u].first+;
a[v].second = v;
dfs(v);
maxndeep[u] = max(maxndeep[u], maxndeep[v]);
}
tout[u] = tim;
} int rt[M], ls[M*logn], rs[M*logn], T[M*logn]; struct Segtree {
int sz;
int alloc(int u) {
T[sz] = T[u], ls[sz] = ls[u], rs[sz] = rs[u], T[sz] = T[u];
return sz ++;
}
void init() {
rt[nill] = ls[nill] = rs[nill] = , T[nill] = inf;
sz = ;
}
void ins(int &o,int u,int l,int r,int x,int val) {
o = alloc(u);
T[o] = min(T[o], val);
if (l==r) return;
int mid = l+r>>;
if (x<=mid) ins(ls[o],ls[u],l,mid,x,val);
else ins(rs[o],rs[u],mid+,r,x,val);
}
int ask(int o,int l,int r,int pl,int pr) {
if (pl<=l&&r<=pr) return T[o];
int mid = l+r>>;
if (pl<=mid && pr>mid) return min(ask(ls[o],l,mid,pl,pr), ask(rs[o],mid+,r,pl,pr));
if (pl<=mid) return ask(ls[o],l,mid,pl,pr);
return ask(rs[o],mid+,r,pl,pr);
}
}sgt; int solve(int x,int c) {
int l = deep[x], r = maxndeep[x], ret = -;
//printf ("maxndeep(%d)=%d\n", x, maxndeep[x]);
//printf ("pl=%d,pr=%d\n", tin[x], tout[x]);
//printf ("%d,%d:l=%d,r=%d\n", x,c,l,r);
while (l <= r) {
int mid = l+r>>;
//printf ("ask(%d)=%d\n", mid, sgt.ask(rt[mid],1,n,tin[x],tout[x]));
if (sgt.ask(rt[mid],,n,tin[x],tout[x]) > c) {
ret = mid, l = mid+;
} else r = mid-;
}
//printf ("ret=%d\n", ret);
return ret==- ? : ret - deep[x] + ;
} int main () {
//freopen("2.in", "r", stdin);
//freopen("22.out","w",stdout);
while (~scanf("%d%d", &n,&Q)) {
for (int i=; i<=n; ++i) {
g[i].clear();
scanf ("%d", val+i);
}
for (int i=, u; i<=n; ++i) {
scanf ("%d", &u);
g[u].push_back(i);
}
a[] = make_pair(, );
deep[] = ;
tim = ;
dfs();
sort(a+, a++n);
sgt.init();
for (int i=,j=; i<=maxndeep[]; ++i) {
rt[i] = rt[i-];
while(j<=n && a[j].first == i) {
sgt.ins(rt[i],rt[i],,n,tin[a[j].second], val[a[j].second]);
++j;
}
}
//puts("------------------");
int x, c;
while (Q --) {
scanf ("%d%d", &x,&c);
printf ("%d\n", solve(x,c));
}
}
return ;
}
3.CS考四级（lyf）
后缀自动机，本来想教下16级小朋友的，然后好像没有时间了，大概留下个坑，让他们自己填吧，hhhhh
首先把每个串按照 #s1#s2#s3#....sn差到sam里，（这里的#指标是特殊字符而已，我的模板里通过Inskey()函数来实现）
对于sam里的叶子节点可以通过len(i)数组和 #s1#s2#s3#....sn进行映射，找到对应的id
然后我们维护sam里的每个节点的 （min(id), max(id))即可，如果这两个值出现在同一个字符串s(i)里，那么对于当前这个节点来说，
它所有可以接受的串都是s(i)的特征串
因为题目要求每个串字典序最小的，所以再dfs处理下就好了
总体复杂度：O(segma(s(i))
//注意：因为 sam 在头部插入了一个 nill 字符（如果没有nill，right集会少
//所以对于 parent树 的叶子：
//如果 l(leaf) == l(fa(leaf)) + 1, 那么说明实际上从 fa(leaf) -> leaf这条边实际上是通过走 nill 字符通过的，
//及原串实际上是不会走到这个节点的。
//hdu6194
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int M = 2e5 + ;
int n;
char s[M];
int col[M<<];
string ans[M]; struct SAM {
static const int kN = M << ;
static const int chN = ;
int fa[kN];
int go[kN][chN];
int l[kN];
int o;
int rt;
int lst; inline int newNode(int _l) {
for (int i=; i<chN; ++i) {
go[o][i] = -;
}
l[o] = _l;
return o ++;
}
void Init() {
o = ;
rt = lst = newNode();
fa[rt] = -;
}
inline void InsKey() {
int p = lst, np = newNode(l[lst]+); lst = np;
fa[np] = rt;
}
inline void Ins(int c) {
int p = lst, np = newNode(l[lst]+); lst = np;
//printf ("%c:%d\n", c+'a', np);
while (~p && go[p][c] == -) go[p][c] = np, p = fa[p];
if (p==-) fa[np] = rt;
else {
int q = go[p][c];
if (l[p]+ == l[q]) fa[np] = q;
else {
int nq = newNode(l[p]+);
//printf ("%c:%d\n", c+'a', nq);
memcpy(go[nq], go[q], sizeof(go[q]));
fa[nq] = fa[q];
fa[q] = fa[np] = nq;
while (~p && go[p][c] == q) go[p][c] = nq, p = fa[p];
}
}
} //topo
int ord[kN];
int cnt[kN];
int right[kN];
int in[kN];
void topo() {
int maxVal = ;
memset (cnt, , sizeof(cnt[])*o);
for (int i=; i<o; ++i) maxVal = max(maxVal, l[i]), ++ cnt[l[i]];
for (int i=; i<=maxVal; ++i) cnt[i] += cnt[i-];
for (int i=; i<o; ++i) ord[-- cnt[l[i]]] = i;
}
int cc[kN][];
vector<char> st;
void dfs(int o) {
if (o!=rt) {
//printf ("%d:(%d,%d), ", o, cc[o][0], cc[o][1]);
//cout << st << endl;
if (cc[o][] == cc[o][] && !cnt[cc[o][]]) {
cnt[cc[o][]] = ;
for (int i=; i<st.size(); ++i) ans[cc[o][]] += st[i];
//ans[cc[o][0]] = st;
}
}
for (int i=; i<; ++i) if (go[o][i]!=-){
st.push_back('a'+i);
dfs(go[o][i]);
st.pop_back();
}
}
void solve() {
//for (int i=1; i<o; ++i) printf ("fa(%d)=%d\n", i, fa[i]);
topo();
memset (cnt, , sizeof(cnt[])*o);
memset (in, , sizeof(in[])*o);
for (int i=; i<o; ++i) ++in[fa[i]];
for (int i=; i<o; ++i) {
if(!in[i]) {
//printf ("%d:l=%d,col=%d\n", i, l[i], col[l[i]-1]);
cc[i][] = cc[i][] = col[l[i]-];
} else {
cc[i][] = inf, cc[i][] = -inf;
}
}
for (int i=o-; i>; --i) {
int f = fa[ord[i]];
cc[f][] = min(cc[f][], cc[ord[i]][]);
cc[f][] = max(cc[f][], cc[ord[i]][]);
}
st.clear();
dfs(rt);
}
} sam; int main () {
//freopen("3.in", "r", stdin);
//freopen("3.out", "w", stdout);
while (~scanf("%d", &n)) {
sam.Init();
int len = ;
for (int i=; i<n; ++i) {
ans[i].clear();
sam.InsKey();
col[len ++] = i;// ????
scanf ("%s", s);
for (int j=; s[j]; ++j) {
sam.Ins(s[j]-'a');
col[len ++] = i;
}
}
sam.solve();
for (int i=; i<n; ++i) {
if (ans[i].empty()) puts("-1");
else cout << ans[i] << endl;
}
}
return ;
}
/*
2
aba
ab 2
ab
ab 2
bd
ad 4
abd
bdc
ddd
abab
*/
4.这不珂学 (lyf)
莫队+莫比乌斯容斥
大概高年级所有人都会求 n 个数的互质对数吧？（不会的话，请先去学这个）。
然后你会发现算贡献的时候，其实就只和每个数的约数有关系，所以一个个算显然也是没有问题的。。。然后就没了
总体复杂度：O(n*sqrt(n)*60)，60是因为1e4以内的数约数数量的最大值是60
#include<bits/stdc++.h>
using namespace std;
const int M = 1e5 + ;
const int block = ;
typedef long long ll; vector<int> yue[M];
vector<bool> isprime;
vector<int> mu;
void sieve () {
isprime.assign(M, true);
isprime[] = isprime[] = false;
for (int i=; i<M/i; ++i) if (isprime[i]) {
for (int j=i*i; j<M; j+=i) {
isprime[j] = false;
}
}
mu.assign(M, );
for (int i=; i<M; ++i) if (isprime[i]) {
if (i<M/i) {
for (int j=i*i; j<M; j+=i*i) mu[j] = ;
}
for (int j=i; j<M; j+=i) mu[j] *= -;
}
for (int i=; i<M; ++i) {
for (int j=i; j<M; j+=i) {
yue[j].push_back(i);
}
}
} int n, m;
int a[M];
int ans[M];
int cnt[M];
int l, r;
int nowAns; struct Query {
int l, r;
int id;
bool operator < (const Query &rhs) const {
if (l/block == rhs.l/block) {
return r < rhs.r;
}
return l < rhs.l;
}
}qu[M]; void Move(int x,int tp) {
//printf ("a(%d)=%d, tp=%d\n", x, a[x], tp);
if (tp==) {
for (int i=; i<yue[a[x]].size(); ++i) {
int &v = yue[a[x]][i];
//printf ("cnt(%d)=%d\n",v , cnt[v]);
nowAns += 1ll*mu[v]*cnt[v];
++cnt[v];
}
} else {
for (int i=; i<yue[a[x]].size(); ++i) {
int &v = yue[a[x]][i];
--cnt[v];
nowAns -= 1ll*mu[v]*cnt[v];
}
}
//printf ("nowAns=%I64d\n", nowAns);
} void solve() {
sort(qu, qu+m);
l = r = nowAns = ;
for (int i = ; i < m; ++i) {
const Query &q = qu[i];
while (l > q.l) Move(--l, );
while (r < q.r) Move(++r, );
while (l < q.l) Move(l++, -);
while (r > q.r) Move(r--, -);
ans[q.id] = nowAns;
}
} int main () {
sieve();
//freopen("4.in", "r", stdin);
//freopen("4.out", "w", stdout);
while (~scanf ("%d%d", &n,&m)) {
for (int i=; i<=n; ++i) {
scanf ("%d", a+i);
}
for (int i=; i<m; ++i) {
scanf ("%d%d", &qu[i].l, &qu[i].r);
qu[i].id = i;
}
memset (cnt, , sizeof(cnt));
solve();
for (int i=; i<m; ++i) {
printf ("%d\n", ans[i]);
}
}
return ;
}
/*
4 2
15 10 6 7
1 3
2 4
*/
5. 情人节的阻击 (lyf)
这种xjb题目区域赛经常会出
分成两类讨论：
一类是贴角放，尽量放成正方形的；
另外就是沿着短一点的边放
#include<bits/stdc++.h>
using namespace std;
int n, m, x, y; int work(int x) {
int f = sqrt(x);
if (f*f>=x) return *f;
if (f*(f+)>=x) return *f+;
return *(f+);
} int main () {
//freopen("5.in", "r", stdin);
//freopen("5.out", "w", stdout);
while (~scanf("%d%d%d%d", &n,&m,&x,&y)) { if (n>m) swap(n, m);
if (x>y) swap(x, y);
int ans1 = ;
if (x/n < ) ans1 = x + ;
else ans1 = (x%n>) + n;
printf ("%d\n", min(ans1, work(x)));
}
return ;
}
/*
1 2 1 1 2 4 2 6 2 4 4 4 3 4 4 8 3 4 3 9
*/
6.男生女生配（lyf）
树状数组
灵儿当时来问了这题这么做，感觉看着对话可能更容易理解：
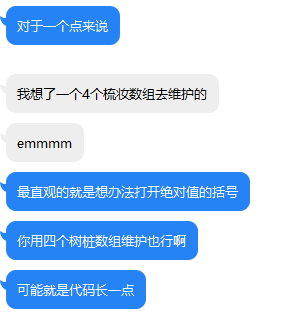
其实就是因为每个点和它左下角的点的曼哈顿距离可以通过：x1+y1 - (xi+yi)来求
总体复杂度：O((n+m)*log(200000))
#include<bits/stdc++.h>
using namespace std;
const int M = +;
const int DJ = +;
const int inf = 0x3f3f3f3f;
int n, m;
struct Node {
int x, y, tp, id;
}a[M<<];
int ans[M]; int c[M];
void init() {
memset(c, -, sizeof(c[])*M);
}
void ins(int x,int v) {
for (int i=x; i<M; i+=i&-i) c[i] = max(c[i], v);
}
int ask(int x) {
int ret = -;
for (int i=x; i>; i-=i&-i) ret = max(ret, c[i]);
return ret;
}
void change() {
for (int i=; i<n+m; ++i) {
int tmp = a[i].x;
a[i].x = DJ-a[i].y;
a[i].y = tmp;
}
} bool cmp(const Node &a,const Node &b) {
if (a.x==b.x) {
if (a.y==b.y) return a.tp<b.tp;
return a.y<b.y;
}
return a.x<b.x;
}
void update() {
init();
sort(a, a+n+m, cmp);
for (int i=; i<n+m; ++i) {
if (a[i].tp==) {
ins(a[i].y, a[i].x+a[i].y);
} else {
int ret = ask(a[i].y);
if (ret!=-) ans[a[i].id] = min(ans[a[i].id], a[i].x+a[i].y-ret);
}
}
} int main () {
//freopen("6.in", "r", stdin);
//freopen("6.out", "w", stdout);
while (~scanf("%d", &n)) {
for (int i=; i<n; ++i) {
scanf ("%d%d", &a[i].x,&a[i].y);
a[i].tp = ;
}
scanf("%d", &m);
for (int i=; i<m; ++i) {
scanf ("%d%d", &a[i+n].x,&a[i+n].y);
a[i+n].tp = ;
a[i+n].id = i;
}
memset(ans, inf, sizeof(ans[])*m);
for (int i=; i<; ++i) {
if (i) change();
update();
}
for (int i=; i<m; ++i) {
printf ("%d\n", ans[i]);
}
//printf ("%d\n", ans[0]);
}
return ;
}
/*
2
1 1
3 3
1
2 4
*/
7.光梯(Noland)
有题意可知，对最后一个点造成影响的点是它前面k个点点，如果知道他前面k个点的期望，在求出每个点走到最后一个点走到这个点的概率，那么就可以求出最后一个点的期望，
如何求出前k个点走到最后一个点所占的比率，假设已知前n-1个点的期望，当只能走到下标为n-k的点时，将会有1/k的部分走到最后一个点，当只能走到下标为n-k+1的点时，还
剩余整体的（k-1）/k,然后又1/(k-1)的概率走到最后一个点，然后可以知道每个点走到最后一个点的概率都是1/k，所有就是前k个点的和除以k，因为这题n和q比较大，但是k比
较小，可以先打表得到所有的值，然后对于询问直接输出即可。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+;
const int M = ;
double dp[M][N];
void init(){
memset(dp,,sizeof(dp));
for(int i = ;i < M;i ++){
double sum = ;
for(int j = ;j < N;j ++){
sum += dp[i][j-];
int res = min(i,j);
if(j > i){
sum -= dp[i][j-min(i,j)-];
}
dp[i][j] = sum / min(i,j)+;
}
}
} int main(){
init();
freopen("7.in","r",stdin);
freopen("7.out","w",stdout);
int n,k;
while(scanf("%d %d",&n,&k)==){
printf("%.3f\n",dp[k][n]);
}
return ;
}
8.magic number（xufei）
看着题目，其实很容易发现 小于等于 S 的都是magic, 然后对于大于 S的，最多只要往上跑 9*9 暴力判就好了，因为1e9里内所有位的和最大值撑死也就 81
9.科学计数法
比赛的时候，我一直在想，为啥大家都怼着A，不做这题。。。。。
10.我好方
我连公式都给了啊！！！为什么还有wa的！！！！
11.不要方
这道题其实是个面试题
我们把矩形的四条边称作(上，下，左，右),
然后对于(上1，上2）选靠下边的线，对于（下1，下2）选靠上边的线
对于(左1，左2）选靠右的线，对于（右1，右2）选靠左的线
然后只要这新的四条线，有交集，那个交集的面积就是答案了。
（PS:其实因为数据很小，你暴力模拟染色技术也能过）
12.丢手绢(baobao)
你把正n边形，和正n-1边形随便找个点拆开来，铺成一条线，然后很容易发现规律。。。。
然后比赛的时候有人用 O(1e9)过了，好像还是我们学校的小伙子，hhhh
具体证明如下：
假设现在有两种点，第一种点是有n个点的，第二种有n-1个点的，假设这两种点的第一个点是重合的，很容易证第2种点的第i个在第1种点的第i个和第i+1之间，在第二种点中，当i小于（n+1）/2时，距离它最近的第一种点事第i个点，当i大于（n+1）/2时，距离它最近的点事第i+1个点，当i等于（n+1）/2时，它距离第i个和第i+1个点的距离是相同的，可以发现每个点离得最近的点没有重复的，所有每个点移动到它最近的点就好了，计算距离的时候，当i小于（n+1）/2时，距离他最近的点的距离是(i-1)/(n*(n-1))，这就是一个等差数列，大于（n+1）/2的点也一样，然后等差数列求和就好了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const double eps = 1e-;
ll n; int main () {
while (~ scanf("%lld", &n)) {
if (n<=) {
puts("");
continue;
}
double x = 1.0/n, y = 1.0/(n-);
ll f = (n-)/;
double ans = (+f)*f/2.0*(y-x)*;
//cout << ans << endl;
ans -= 0.5 - 1.0/n*(n/);
printf ("%.0f\n", ans*+eps);
}
return ;
}
2017zstu新生赛的更多相关文章
- SCNU ACM 2016新生赛初赛 解题报告
新生初赛题目.解题思路.参考代码一览 1001. 无聊的日常 Problem Description 两位小朋友小A和小B无聊时玩了个游戏,在限定时间内说出一排数字,那边说出的数大就赢,你的工作是帮他 ...
- SCNU 2015ACM新生赛决赛【F. Oyk闯机关】解题报告
题目大意:一个$N$$\times$$N$的阵列,每个格子有$X_{ij}$个调和之音,若每次只能选择走右边或下边,从左上角出发走到右下角,问最多能收集到多少个调和之音? ...
- Codeforces 801 A.Vicious Keyboard & Jxnu Group Programming Ladder Tournament 2017江西师大新生赛 L1-2.叶神的字符串
A. Vicious Keyboard time limit per test 2 seconds memory limit per test 256 megabytes input standard ...
- [ACTF2020 新生赛]BackupFile && [ACTF2020 新生赛]Upload &&[GYCTF2020]Blacklist
[ACTF2020 新生赛]BackupFile 尝试找到源代码,加上题目是备份文件,猜测备份文件里面有网站的源代码,御剑扫描一下,就扫到index.php 访问index.php.bak 下载源代码 ...
- [BUUCTF]REVERSE——[ACTF新生赛2020]Oruga
[ACTF新生赛2020]Oruga 附件 步骤: 例行检查,64位程序,无壳 64位ida载入,检索字符串,根据提示来到关键函数 14行~18行就是让字符串的前5位是 actf{ ,sub_78A( ...
- [BUUCTF]REVERSE——[ACTF新生赛2020]usualCrypt
[ACTF新生赛2020]usualCrypt 附件 步骤: 例行检查,无壳,32位程序 32位ida载入,直接看main函数 逻辑很简单,一开始让我们输入一个字符串,然后该字符串经过sub_4010 ...
- [BUUCTF]REVERSE——[ACTF新生赛2020]rome
[ACTF新生赛2020]rome 附件 步骤 无壳,32位程序 32位ida载入,根据提示字符串"You are correct!",找到关键函数func v15 = 'Q'; ...
- [BUUCTF]REVERSE——[ACTF新生赛2020]easyre
[ACTF新生赛2020]easyre 附件 步骤 查壳,32位程序,upx壳儿 脱完壳儿,扔进ida 分析 一开始给我们定义了一个数组, v4=[42,70,39,34,78,44,34,40,73 ...
- SCNU ACM 2016新生赛决赛 解题报告
新生初赛题目.解题思路.参考代码一览 A. 拒绝虐狗 Problem Description CZJ 去排队打饭的时候看到前面有几对情侣秀恩爱,作为单身狗的 CZJ 表示很难受. 现在给出一个字符串代 ...
随机推荐
- WPF使用HierarchicalDataTemplate绑定Dictionary生成TreeView
Dictionary中的<string, CustomeType>CustomeType是一个集合,将其绑定生成一棵树,树的第一层节点是Dictionary的Key,第二层是Custome ...
- ViewFlow增强onItemClick功能及ViewFlow AbsListView源代码分析
先看实现效果,上图: ViewFlow是一个非常好用的,用于不确定item个数的水平滑动切换的开源项目. 可是从github上下载的ViewFlow事实上是不支持onItemClick功能的,tou ...
- python day- 16 面向对象
1.类的相关知识 类:是指具有相同属性和技能的一类事物. 比如:人类 ,植物类,动物类,狗类. 对象:是类中的某一个实例,是类的具体表现. 比如:具体到某个人,某一个植物,某一条狗. class 是p ...
- hibernate 的POJO状态
瞬时状态 刚new出来的对象,还没和session发生联系,或者delete之后的对象 持久化状态 用save,get等方法保存或获取到session中的对象,和数据保持一一对应的关系 脱管状态 对象 ...
- Mac OS安装Scrapy
个人觉得掌握简单的爬虫知识非常有用,特别是想要从一些特定网站自动地下载一些资源或者统计一些数据,非常的有用.对于产品经理来说,如果要了解竞争产品.替代产品的价格,可以写一个爬虫脚本从各大电商网站爬取相 ...
- 定时任务Timer
一.Timer介绍 java.util.Timer java.util.TimerTask Timer是一个定时器类,通过该类可以为指定的定时任务进行配置.TimerTask类是一个定时任务类,该类实 ...
- Vue : props 使用细节(父组件传递数据给子组件)
props使用细节 在Vue.js中我们可以使用 props 实现父组件传递数据给子组件,下面我们总结一下props的使用细节 1.基础类型检查 2.必填数据 3.默认值 4.自定义验证函数 其中每一 ...
- POJ1077 Eight —— IDA*算法
主页面:http://www.cnblogs.com/DOLFAMINGO/p/7538588.html 代码一:像BFS那样,把棋盘数组放在结构体中. #include <iostream&g ...
- poj 2531 Network Saboteur 解题报告
题目链接:http://poj.org/problem?id=2531 题目意思:将 n 个点分成两个部分A和B(也就是两个子集啦), 使得子集和最大(一定很难理解吧,呵呵).举个例子吧,对于样例,最 ...
- codeforces C. Magic Formulas 解题报告
题目链接:http://codeforces.com/problemset/problem/424/C 题目意思:给出 n 个数:p1, p2, ..., pn,定义: q1 = p1 ^ (1 mo ...