HDU 5863 cjj's string game ( 16年多校10 G 题、矩阵快速幂优化线性递推DP )

题目链接

题意 : 有种不同的字符，每种字符有无限个，要求用这k种字符构造两个长度为n的字符串a和b，使得a串和b串的最长公共部分长度恰为m，问方案数

分析 :

直觉是DP

不过当时看到 n 很大、但是 m 很小的时候

发现此题DP并不合适、于是想可能是某种组合数学的问题可以直接公式算

看到题解的我、恍然大悟、对于这种数据、可以考虑一下矩阵快速幂优化的DP

首先要想到线性递推的 DP 式子

最直观的想法就是 dp[i][j] = 到第 i 个位置为止、前面最长匹配长度为 j 的方案数

但是如果仔细想想、这样子的定义状态并不好转移、遂换一种思路

定义 dp[i][j] = 到第 i 个位置为止、以第 i 个字符为结尾的匹配串的长度为 j 的方案数

有转移

dp[i][0] = (dp[i-1][0] + dp[i-1][1] + .... + dp[i-1][m] ) * k * (k-1)   （k * (k-1) 的意义是a、b串第 i 个字符不一样的方案数）

dp[i][j] = dp[i-1][j-1] * k ( j ≤ i )

然后尝试去构造矩阵、此处引用 链接

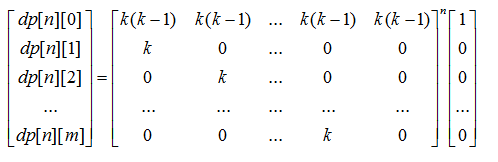
但是注意一下这里的 DP 意义、答案最后并不是 dp[n][m]

dp[n][0] + dp[n][1] + ... + dp[n][m] 可以看成到第 n 个位置为止匹配长度 ≤ m 的方案数

那么如果可以得到匹配长度 ≤ m-1 的方案数两者相减就可以得到匹配长度恰为 m 的方案数了

所以做两次矩阵快速幂即可

#include<bits/stdc++.h>
#define LL long long
#define ULL unsigned long long

#define scl(i) scanf("%lld", &i)
#define scll(i, j) scanf("%lld %lld", &i, &j)
#define sclll(i, j, k) scanf("%lld %lld %lld", &i, &j, &k)
#define scllll(i, j, k, l) scanf("%lld %lld %lld %lld", &i, &j, &k, &l)

#define scs(i) scanf("%s", i)
#define sci(i) scanf("%d", &i)
#define scd(i) scanf("%lf", &i)
#define scIl(i) scanf("%I64d", &i)
#define scii(i, j) scanf("%d %d", &i, &j)
#define scdd(i, j) scanf("%lf %lf", &i, &j)
#define scIll(i, j) scanf("%I64d %I64d", &i, &j)
#define sciii(i, j, k) scanf("%d %d %d", &i, &j, &k)
#define scddd(i, j, k) scanf("%lf %lf %lf", &i, &j, &k)
#define scIlll(i, j, k) scanf("%I64d %I64d %I64d", &i, &j, &k)
#define sciiii(i, j, k, l) scanf("%d %d %d %d", &i, &j, &k, &l)
#define scdddd(i, j, k, l) scanf("%lf %lf %lf %lf", &i, &j, &k, &l)
#define scIllll(i, j, k, l) scanf("%I64d %I64d %I64d %I64d", &i, &j, &k, &l)

#define lson l, m, rt<<1
#define rson m+1, r, rt<<1|1
#define lowbit(i) (i & (-i))
#define mem(i, j) memset(i, j, sizeof(i))

#define fir first
#define sec second
#define VI vector<int>
#define ins(i) insert(i)
#define pb(i) push_back(i)
#define pii pair<int, int>
#define VL vector<long long>
#define mk(i, j) make_pair(i, j)
#define all(i) i.begin(), i.end()
#define pll pair<long long, long long>

#define _TIME 0
#define _INPUT 0
#define _OUTPUT 0
clock_t START, END;
void __stTIME();
void __enTIME();
void __IOPUT();
using namespace std;

;
;

struct MAT{
    LL val[][];
    int sz;
    MAT(){};
    MAT(, sizeof(val)); }
    friend MAT operator * (const MAT & A, const MAT & B){
        MAT C(A.sz);
        ; k <= C.sz; k++)
            ; i <= C.sz; i++){
                ) continue;
                ; j <= C.sz; j++){
                    C.val[i][j] = C.val[i][j] + A.val[i][k] * B.val[k][j] % mod;
                    if(C.val[i][j] >= mod) C.val[i][j] -= mod;
                }
            }
        return C;
    }
};

MAT pow_mod(MAT a, LL b)
{
    MAT ret(a.sz);
    ; i<=ret.sz; i++) ret.val[i][i] = ;
    while(b){
        ) ret = ret * a;
        a = a * a;
        b >>= ;
    }return ret;
}

LL Cal(int n, int m, int k)
{
    MAT A(m+);
    ; i<=A.sz; i++) A.val[][i] = 1LL * k * (k - );
    ; i<=A.sz; i++) A.val[i][i-] = k * 1LL;

    A = pow_mod(A, n);

    LL ret = ;
    ; i<=A.sz; i++)
        ret = (ret + A.val[i][]) % mod;
    return ret;
}

int main(void){__stTIME();__IOPUT();

    int nCase;

    sci(nCase);

    while(nCase--){
        int n, m, k;
        sciii(n, m, k);
        printf(, k) + mod) % mod);
    }

__enTIME();;}

void __stTIME()
{
    #if _TIME
        START = clock();
    #endif
}

void __enTIME()
{
    #if _TIME
        END = clock();
        cerr<<"execute time = "<<(double)(END-START)/CLOCKS_PER_SEC<<endl;
    #endif
}

void __IOPUT()
{
    #if _INPUT
        freopen("in.txt", "r", stdin);
    #endif
    #if _OUTPUT
        freopen("out.txt", "w", stdout);
    #endif
}